A long thin wire carrying a varying current I=i0sinωt lies at a distance y above one edge of a rectangular wire loop of length LandW lying in the x−z plane. What emf is induced in the loop?

The correct Answer is:μ04πi0Wωcosωt1n(L2+y2y2)
The magnetic field at point P [Fig. S3.27(b)] is
B=μ02πi√y2+z2
The magnetic flux through the shaded strip in Fig. S3.27(a) is
dϕ=(Wdz)μ02πi√y2+z2sinθ
where sinθ=z√y2+z2
∴ total magnetic flux through rectangular loop is
ϕ=∫L0μ02πi0sinωtWzdzy2+z2
=μ04π(y2+L2y2)i0sinωt
(a) 
∴ induced emf in the loop is
e=dϕdt=μ04πi0Wωt1n(L2+y2y2)
Alternate method to find flux ϕ:
Flux through the given loop will be same as the flux through a cylindrical region from radius y to radius √L2+y2
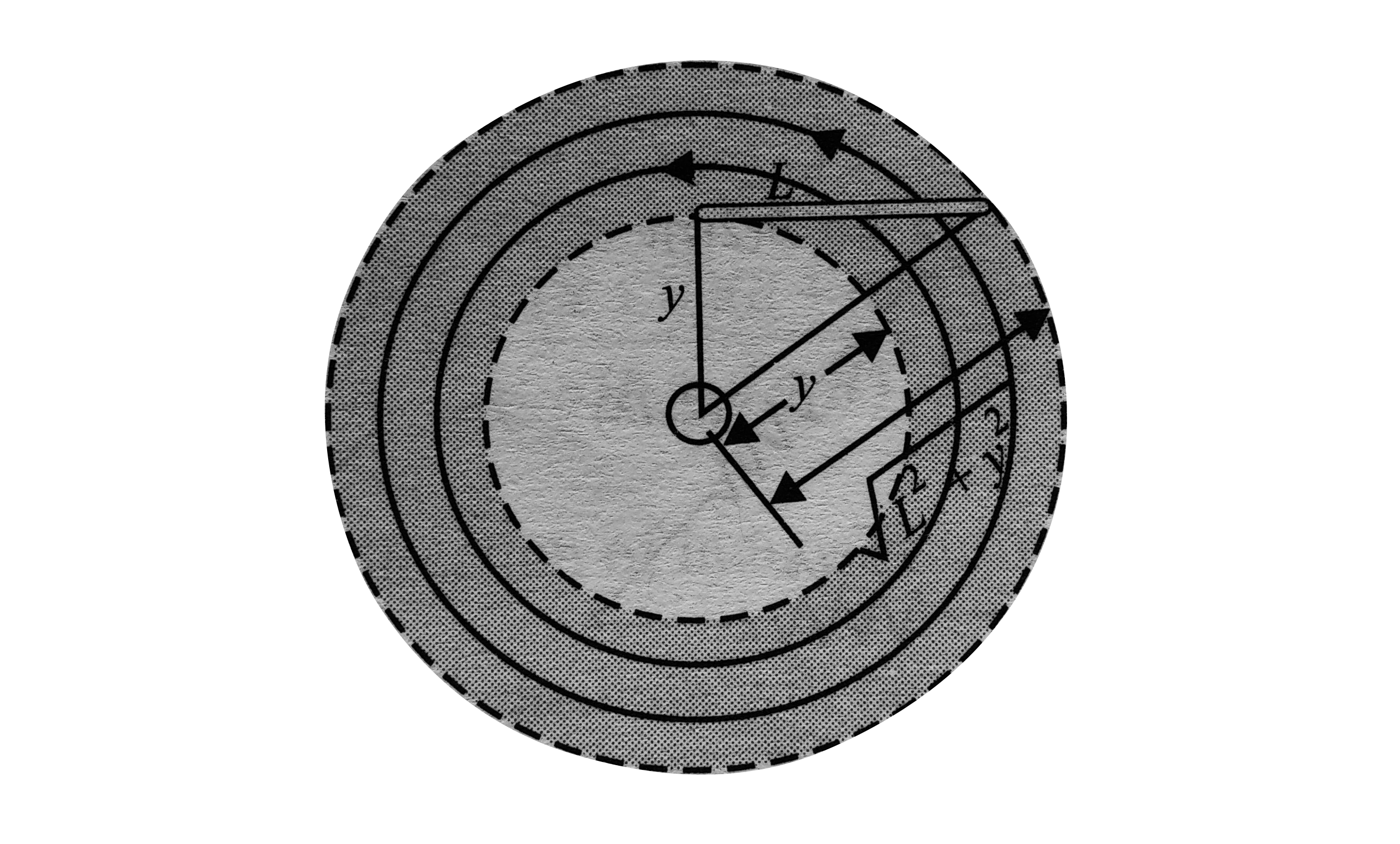
So, ϕ=intμ0i2πxWdx → ϕ=ϕ=μ0i2πW∫√L2+y2dxxy
→ ϕ=μ0(i0sinωt)W2πloge[√L2+y2y]
=μ0W(i0sinωt)4πloge[L2+y2y]
Now induced emf can be found .
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.2
27 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
Find the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
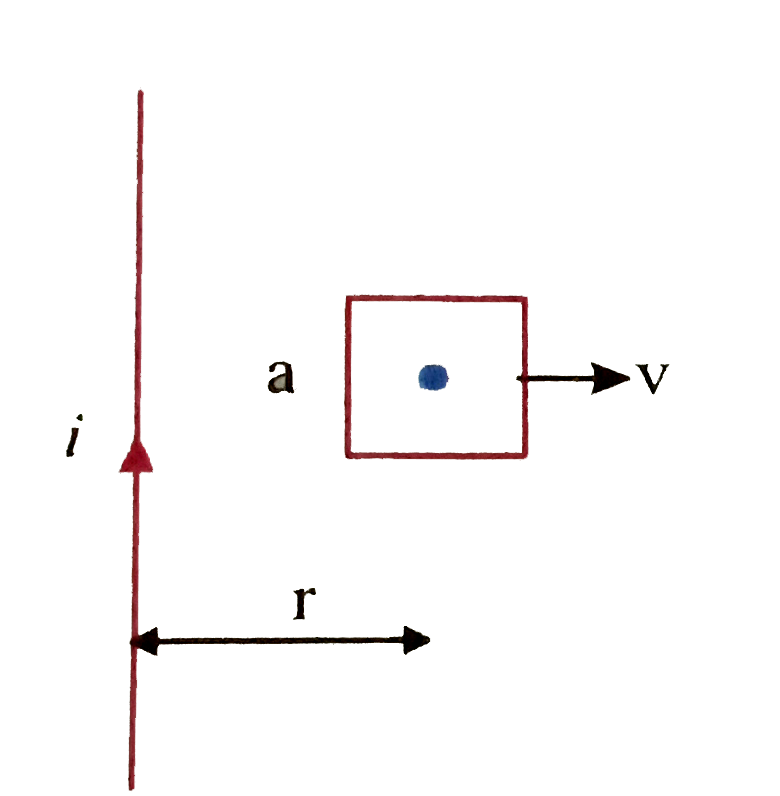
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
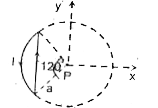
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionFigure shows a long straight wire carrying current I and a square conducting wire loop of side l, at a distance 'a' from current wire. Both the current wire and loop are in the plane of paper. Find the flux of magnetic filed of current wire, passing through the loop.

View SolutionFigure shows a long straight wire carrying current , and a square conducting wire loop of side i, at a distance 'a' from current wire. Both the current wire and loop arc in the plane of paper. Find the flux of magnetic field of current wire, passing through the loop.
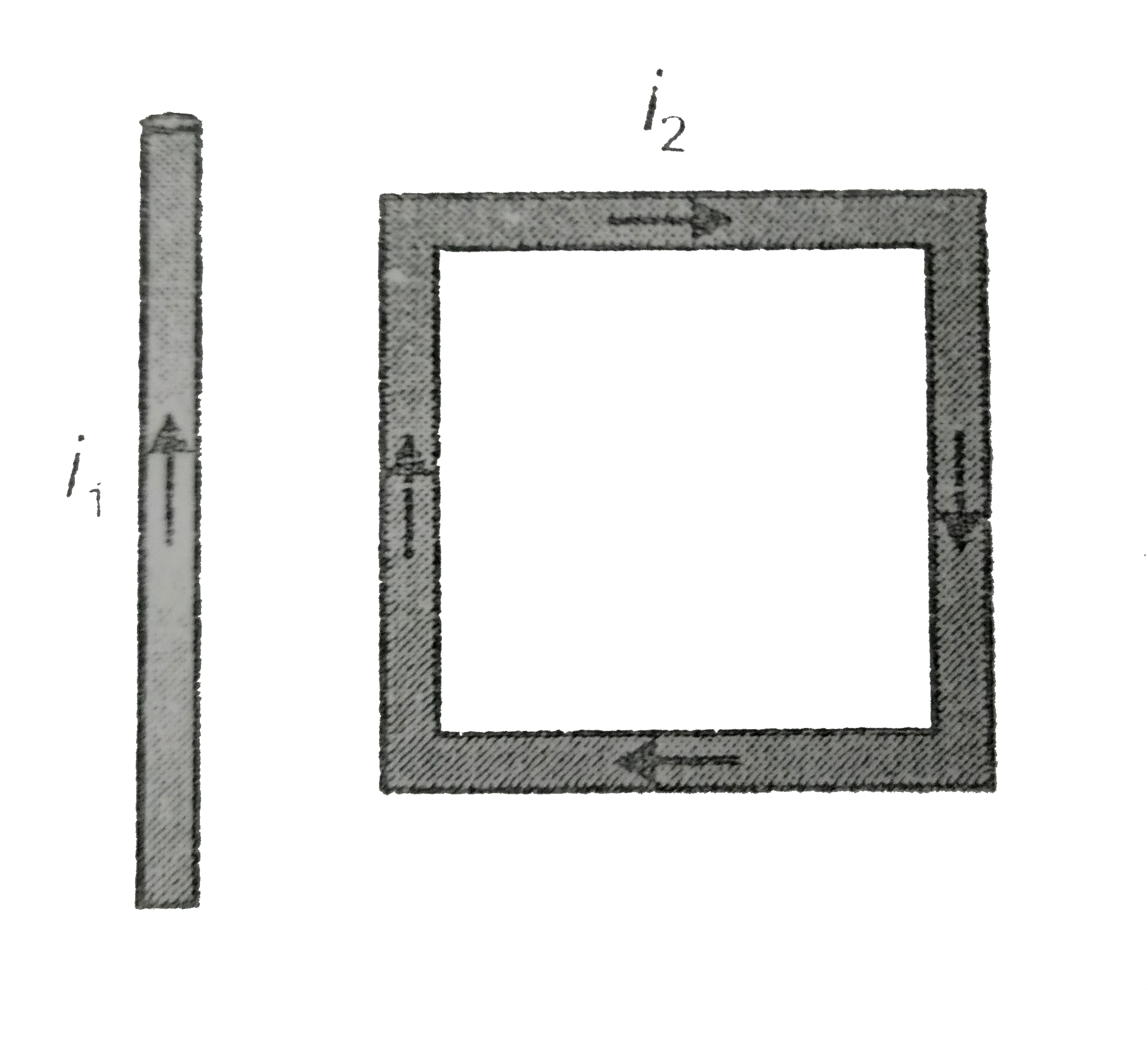
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
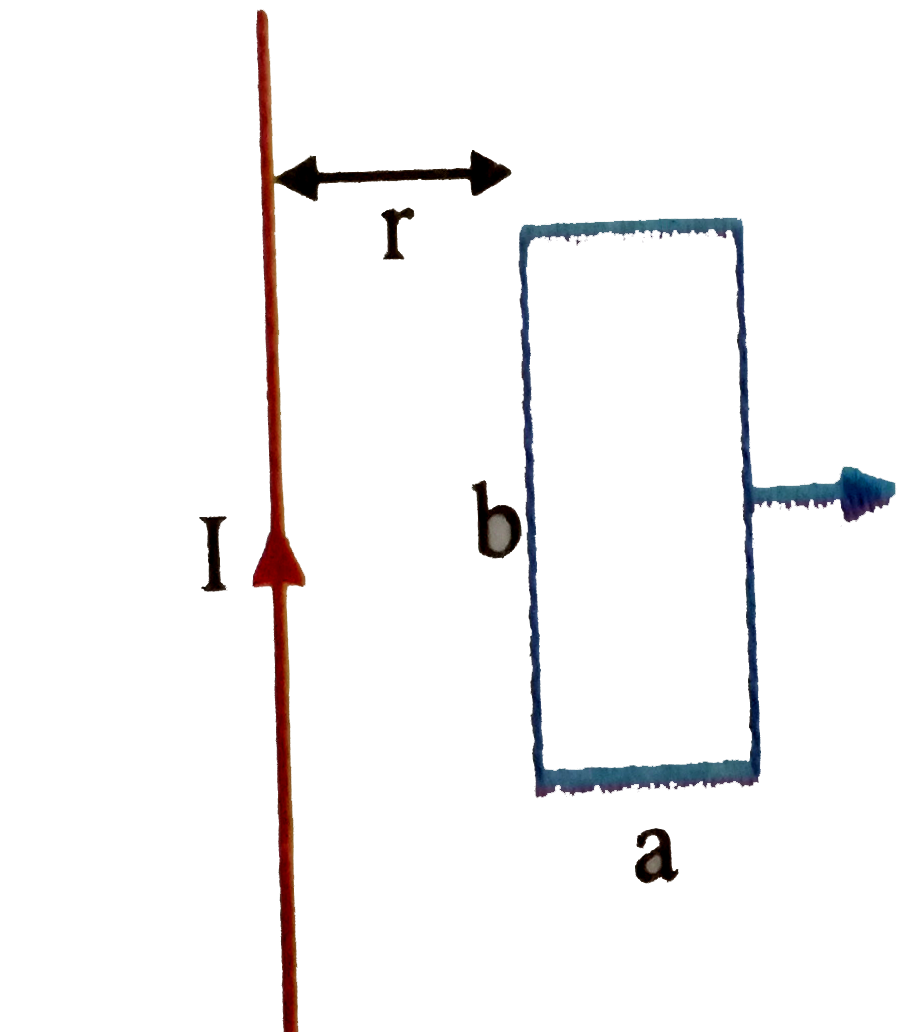
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wire carrying current 'I'. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.

View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View SolutionA rectangular loop of wire of size 4cm×10cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.

View Solution
