Question

A square shaped, conducting wire loop of side $L$, total mass $m$ and total resistance $R$ initially lies in the horizontal $x-y$ plane, with corners at $(x,y,z)=(0,0,0),(0,L,0),(L,0,0),\text{and}(L,L,0)$. There is a uniform upward magnetic field in the space within and around the loop. The side of the loop that extends from $(0,0,0)\to (L,0,0)$ is held in place on the x-axis, the rest of the loop is released, it begins to rotate due to the gravitational torque.
(a) Find the net torque (magnitude and direction)that acts on the loop when it has rotated through an anglr $\varphi$ from its original orientation and is rotating dounward at an angular speed $\omega$.
(b) Find the angular acceleration of the loop at the instant described in part (a).
( c) Compared to teh case with zero magnetic field, does it take the loop a longer or shorter time to rotate through ${90}^{\circ }$ ? Explain.
(d) Is mechanical energy conserved as the loop rotates downward ? Explain.

Answer

(a) `mg(L)/(2)cos phi - (omegaB^(2)L^(4)sin^(2)phi)/(R )`; (b) `(6g)/(5L)cos phi - (12 omega B^(2)L^(2))/(5mR)sin^(2)phi`; (c ) Longer, (d) No

Explanation

(a) magnetic flux passing through the positin when the loop has rotated by an angle `phi`

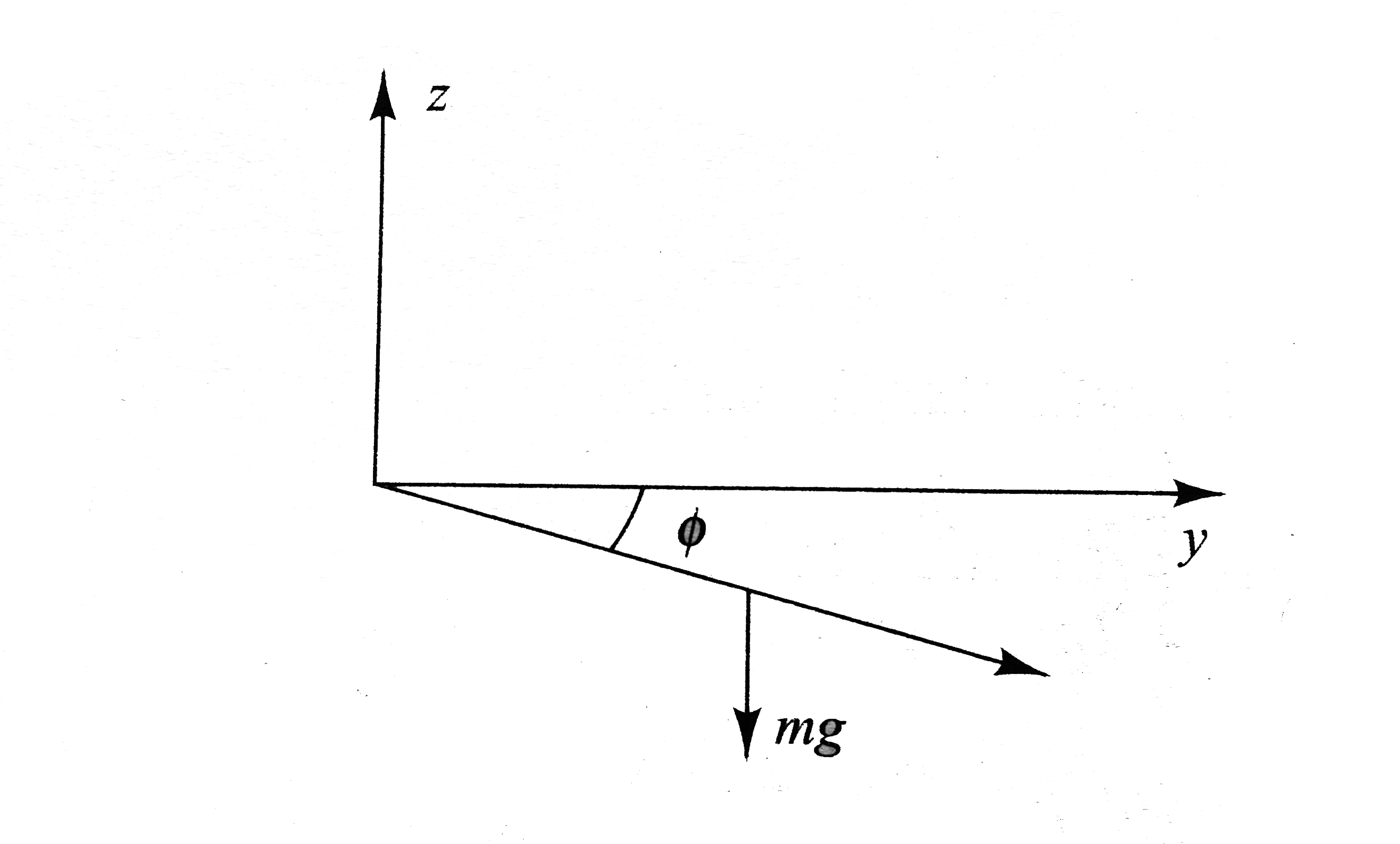
`phi_(mag) = BL^(2) cos theta`
`|e| = (dphi)/(dt) = BL^(2) sin phi (dphi)/(dt)`
`|e| = BL^(2) (sin phi)omega`
Current through the loop, `I = (|e|)/(R) = ( BL^(2) (sin phi)omega)/(R)`
`tau_(mag) = MB sin phi = (IL^(2))B sin phi = (B^(2)L^(4) omegasin^(2)phi)/(R)`
`tau_(gravity) = mg L/2 cos phi`
`tau_(n et) = mg L/2 cos phi - (omegaB^(2)L^(4)sin^(2)phi)/(R)`
(b) `tau_(net) = I alpha`, where `I = (m)/(4)L^(2) + 2((1)/(3)(m)/(4)L^(2)) = (5)/(12)mL^(2)`
`alpha = (tau_(net))/(I) = (6g)/(5L)cosphi - (12omegaB^(2)L^(2))/(5mR)sin^(2)phi`
( c) Longer, because induced emf opposes the motion of the loop.
(d) No, because some energy will convert into heat due to flow of current.