The wire loop, shown in , is made by taking a flat rectangular loop of sides 10cm and 20cm bending at the long sides a their midpoints to produce two mutually perpendicular square parts. The loop is laced in an oscillating magnetic field B=B0sin2πvt, with B0=1.2×10−3T and v=60Hz. The magnetic field is induced at angle θ with x−z plane.
(a) Express the emf around the loop as a function of time and the angle θ.
(b) For what angle θ does the induced emf have the largest amplitude ?
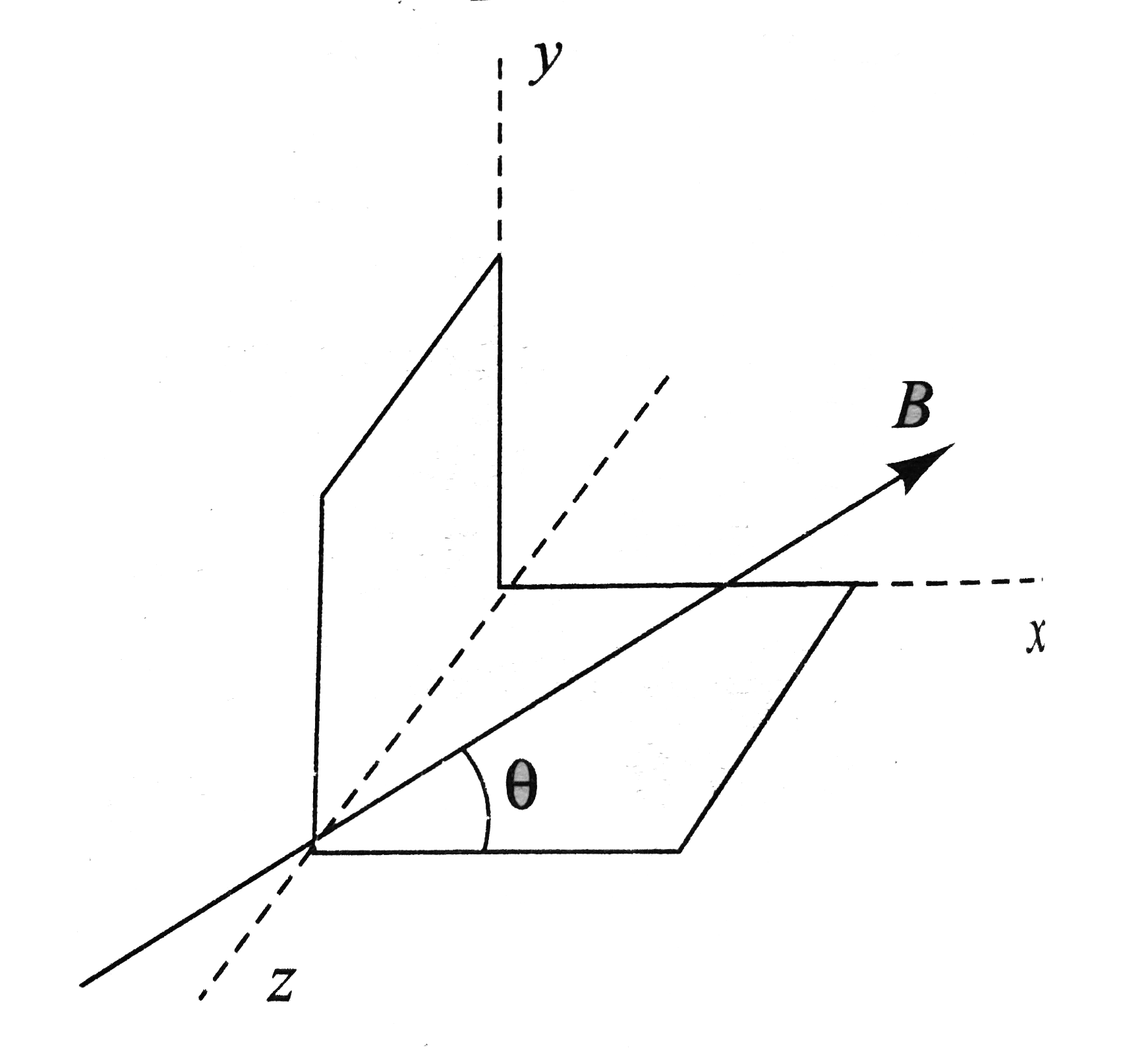
The correct Answer is:(a) (1.44π×10−3)cos(120πt)(cosθ+sinθ)V; (b) π4
(a) 
Now flux through loop (1), ϕ1=Ba2cosθ
Flux through loop (2), ϕ2=Ba2sinθ
emf induced in loop (1),
E1=dϕ1dt=(2πv)B0cos(2πvt)a2cosθ
emf induced in loop (2),
E2=dϕ2dt=(2πv)B0cos(2πvt)a2sinθ
∴ net induced emf, E≠t=E1+E2
=(2πv)B0cos(2πvt)a2(cosθ+sinθ)
=(120π)(1.2×10−3)cos(120πt)(0.01)×(cosθ+sinθ)
=(1.44π×10−3)cos(120πt)(cosθ+sinθ)V
(b) emf will be maximum when cosθ+sinθ has maximum value.
Let y=cosθ+sinθ
dydθ=−sinθ+cosθ=0 → θ=π4
d2ydthη2=−cosθ−sinθ=¬ative at θ=π4, hence at θ=π4,
induced emf is maximum.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.2
27 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View Solution
Knowledge Check
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
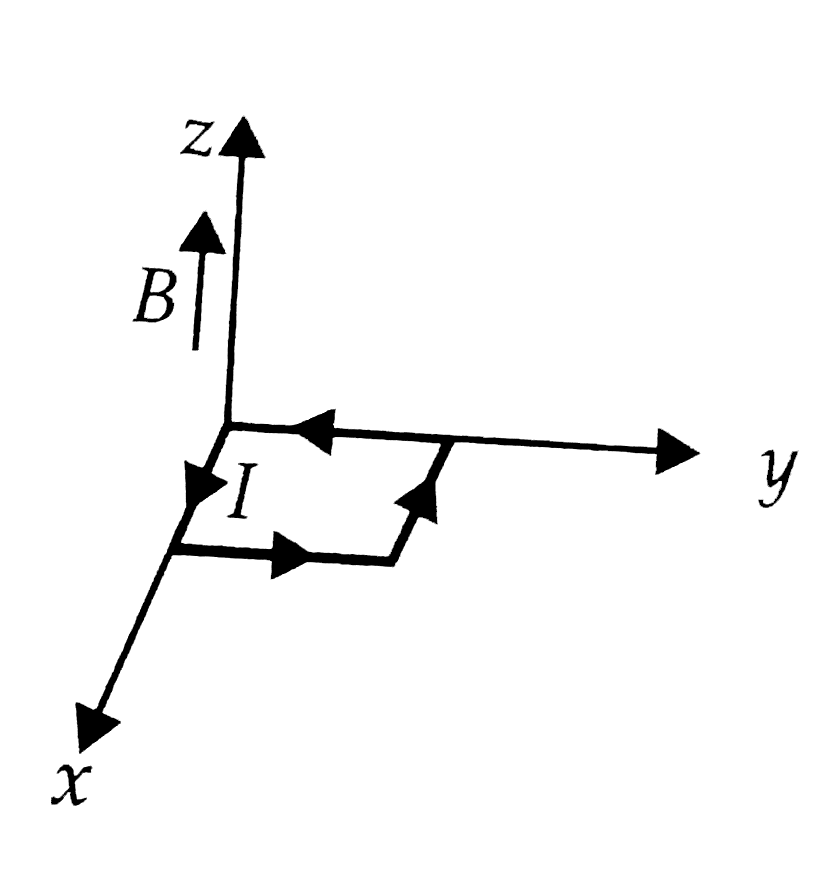 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
Figure shows a square current carrying loop ABCD of side 10 cm and current i = 10A. The magnetic moment of the loop is:

View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

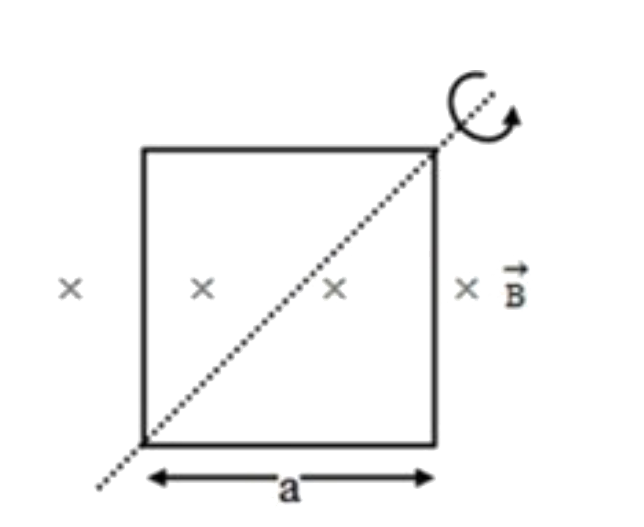
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
View SolutionA square loop of side .a. lying in a perpendicular magnetic field to its plane is changed to a circle. If change occurs in .t. seconds in magnetic field B tesla, the induced emf is
View Solution
