A vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
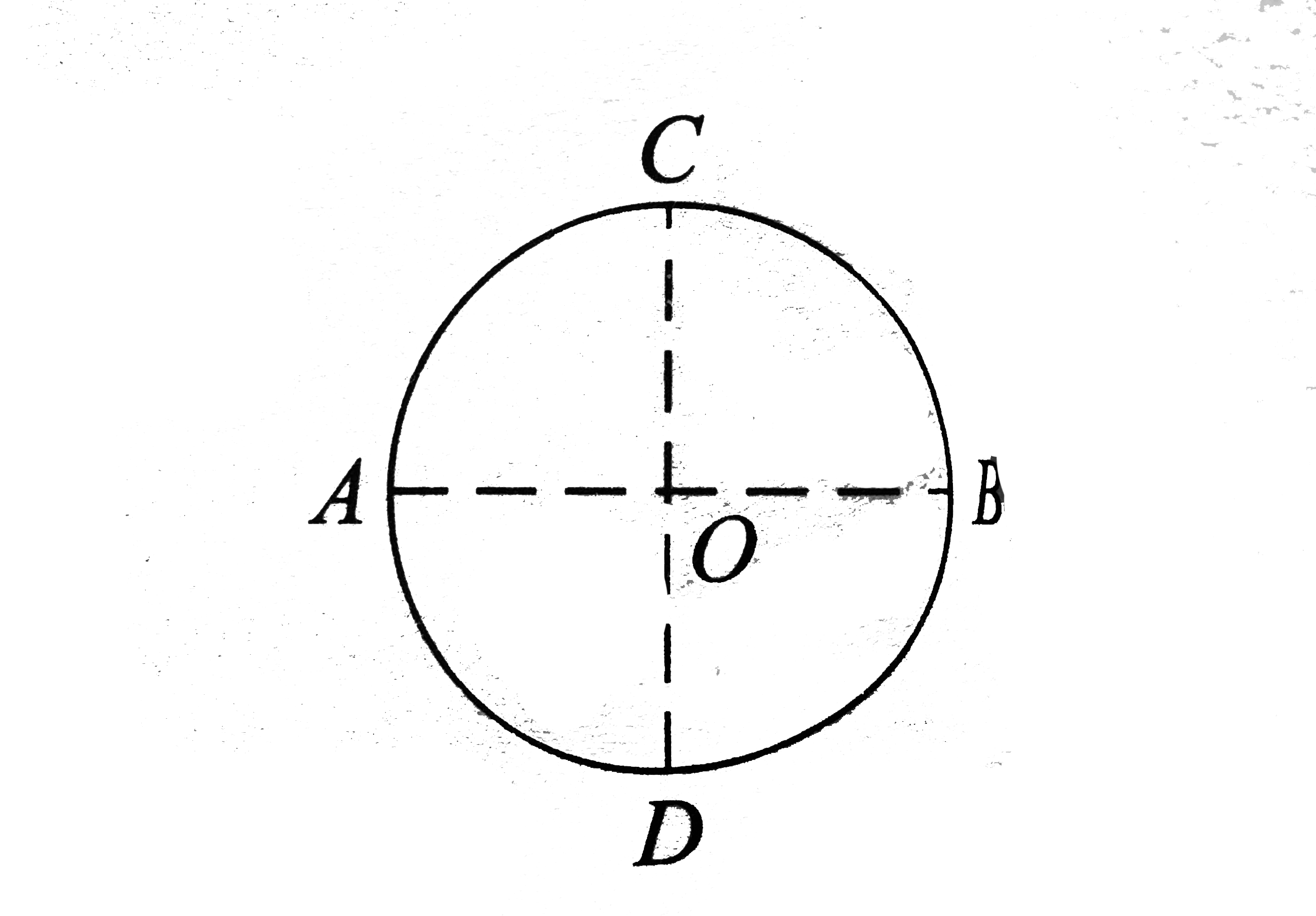
(a) AandB are at the same potential
(b) CandD are at the same potential
( c) current flows in clockwise direction
( d) current flows in anticlockwise direction
The correct Answer is:B
(b) When the ring falls vertically, there will be an induced emf across AandB(e=Bv(2r).
Note that there will be a potential difference across any two points on the ring, and the line joining these has a projected length in the horizontal plane. For example, between points PandQ there is a projected length x in the horizontal plane.
∴ P. D. across P and Q is
V=Bvx
But for points C and D, x=0 Therefore, P.D.=0
Hence (b)
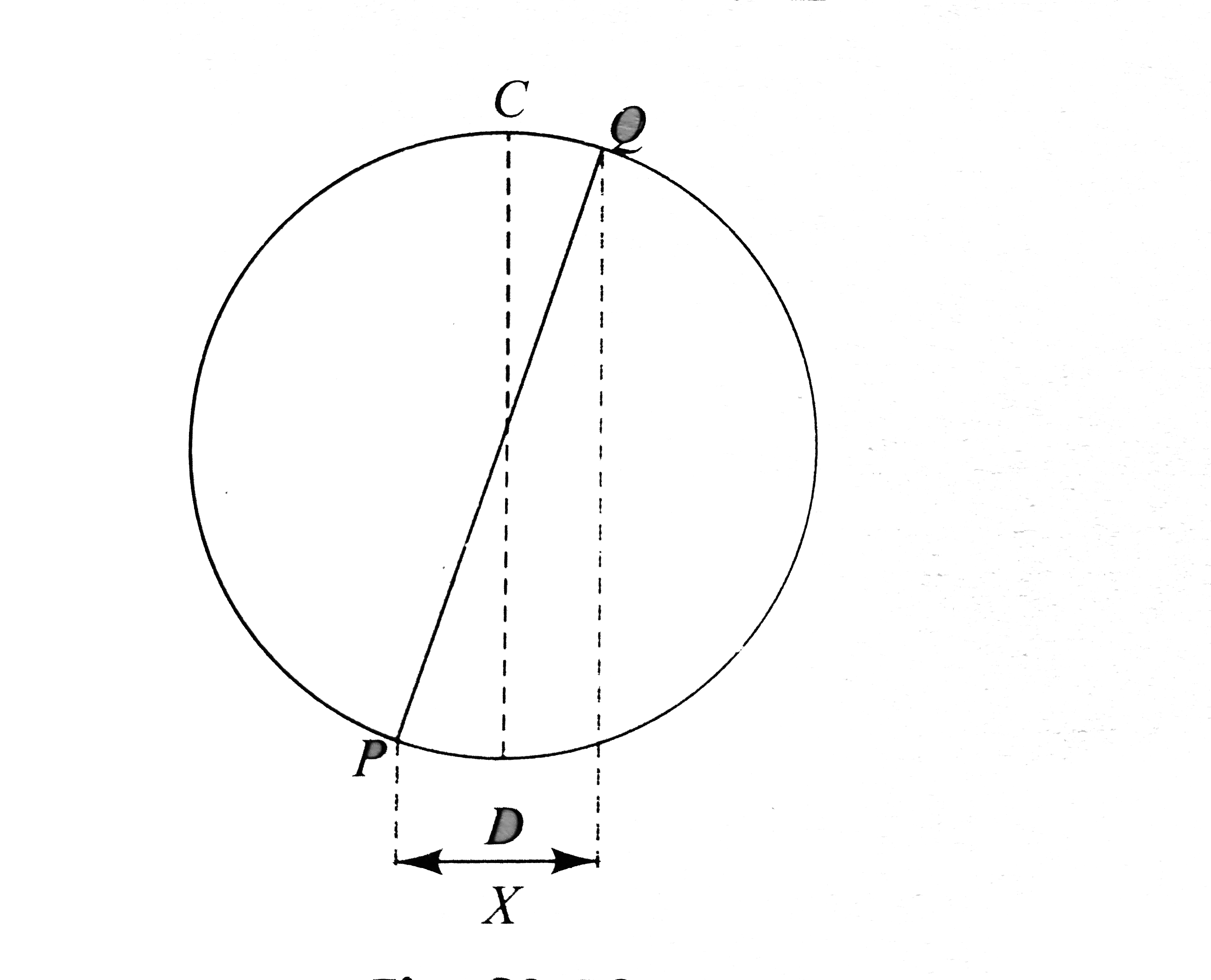
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
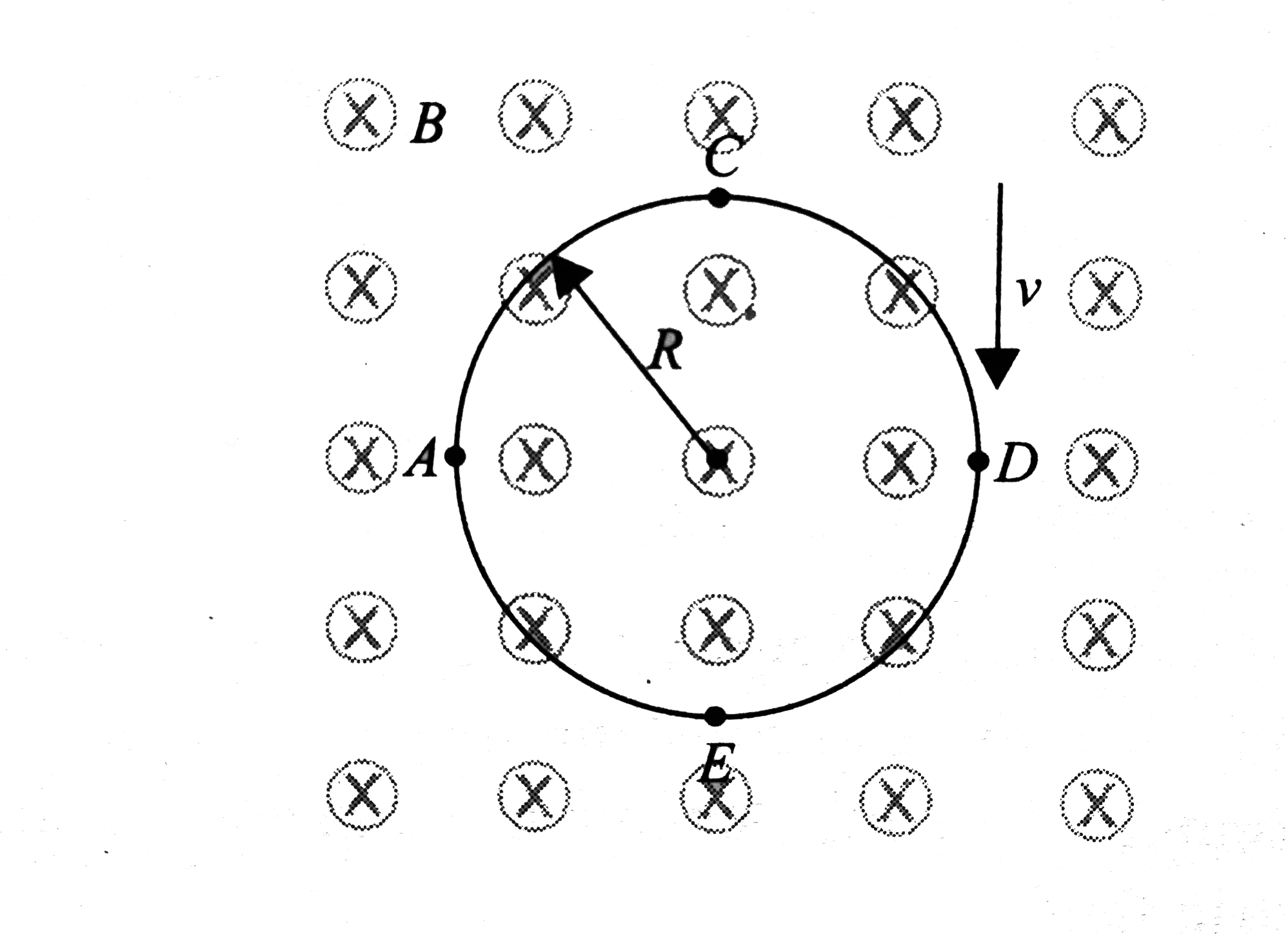
A vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,
View Solution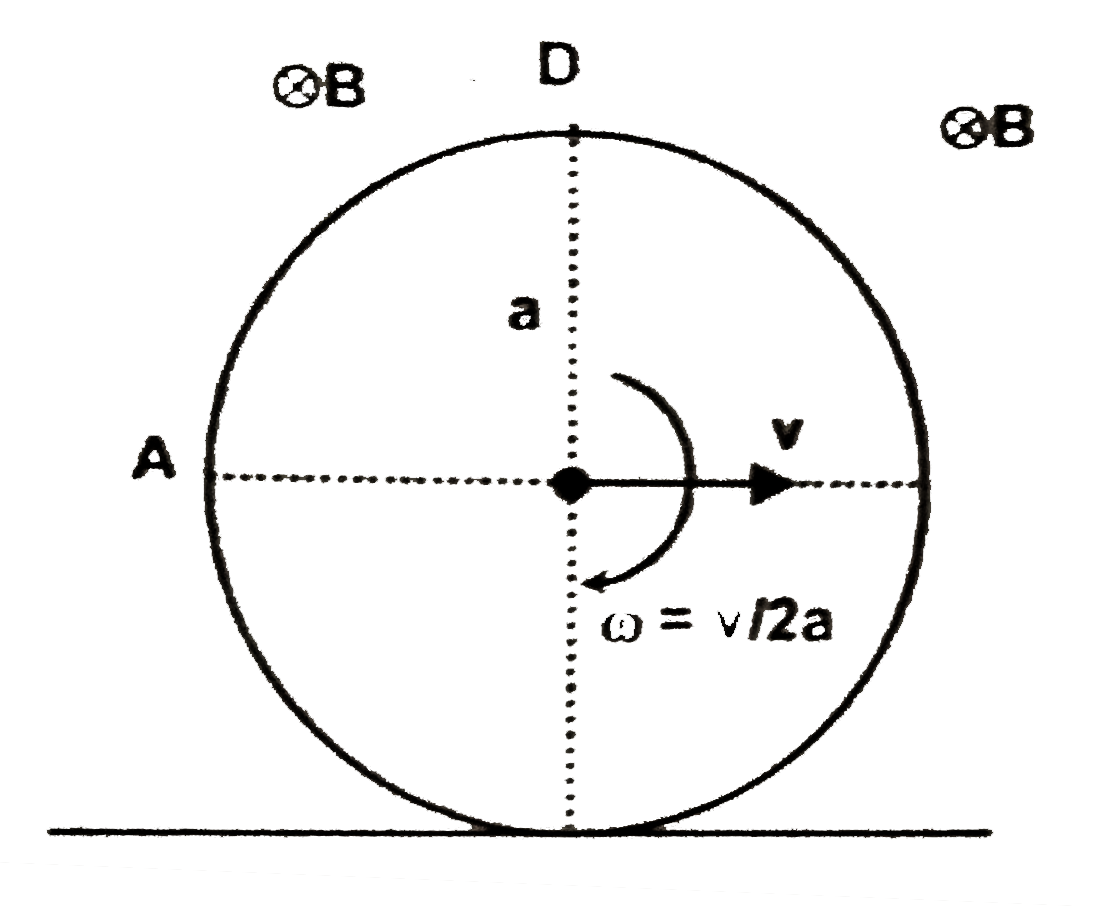
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

View Solutionthe uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionThe figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is

View Solutionthe uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
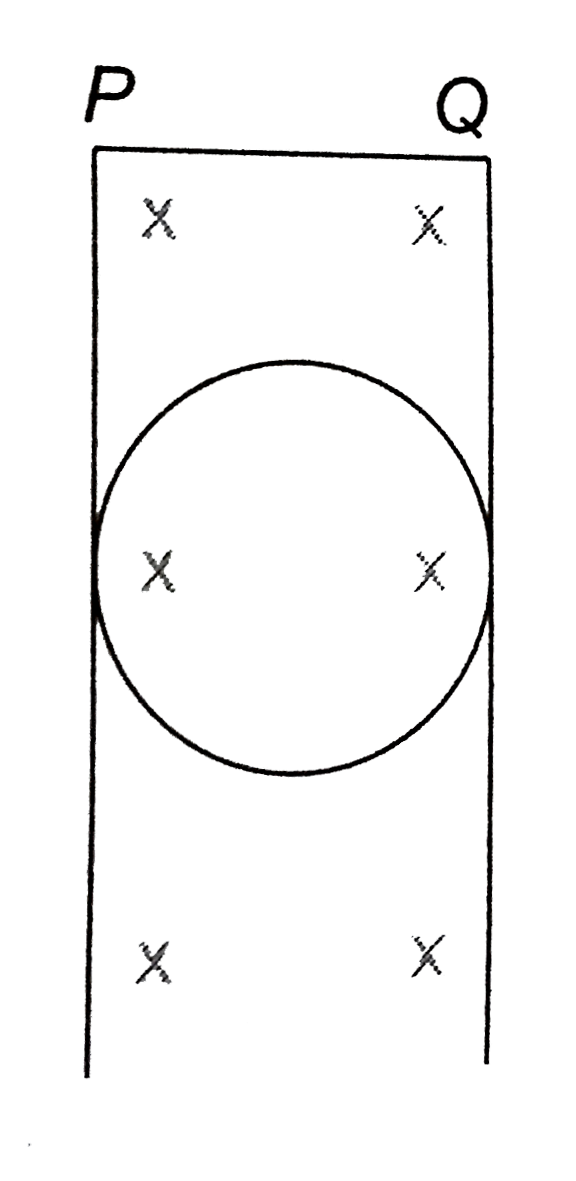
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is

View Solution
