A toy gun a spring of force constant k. When changed before being triggered in the upward direction, the spring is compressed by a distance x. If the mass of the shot is m, on the being triggered it will go up to a height of
kx2mg
x2kmg
kx22mg
(kx)2mg
The correct Answer is:C
To solve the problem, we will use the principle of conservation of energy. The elastic potential energy stored in the spring when it is compressed will be converted into gravitational potential energy when the mass is shot upwards.
1. Identify the Elastic Potential Energy (EPE) of the Spring:
The elastic potential energy stored in a compressed spring is given by the formula:
EPE=12kx2
where k is the spring constant and x is the compression distance.
2. Identify the Gravitational Potential Energy (GPE):
When the mass m is shot upwards to a height h, the gravitational potential energy gained by the mass is given by:
GPE=mgh
where g is the acceleration due to gravity.
3. Apply the Conservation of Energy Principle:
According to the conservation of energy, the elastic potential energy stored in the spring will be equal to the gravitational potential energy gained by the mass when it is shot upwards:
12kx2=mgh
4. Solve for Height h:
Rearranging the equation to solve for h:
h=12kx2mg
Simplifying this gives:
h=kx22mg
5. Final Answer:
Therefore, the height h to which the mass will rise is:
h=kx22mg
The elastic potential energy stored in a compressed spring is given by the formula:
EPE=12kx2
where k is the spring constant and x is the compression distance.
When the mass m is shot upwards to a height h, the gravitational potential energy gained by the mass is given by:
GPE=mgh
where g is the acceleration due to gravity.
According to the conservation of energy, the elastic potential energy stored in the spring will be equal to the gravitational potential energy gained by the mass when it is shot upwards:
12kx2=mgh
Rearranging the equation to solve for h:
h=12kx2mg
Simplifying this gives:
h=kx22mg
Therefore, the height h to which the mass will rise is:
h=kx22mg
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
Two masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
View SolutionTwo blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
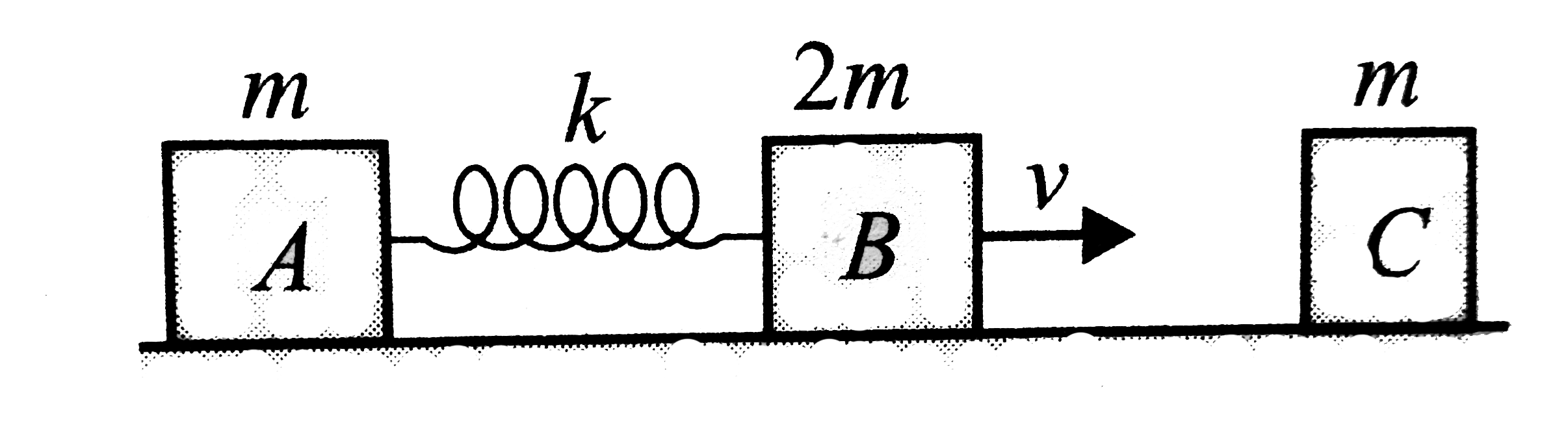
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction.

View Solution
