Two blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
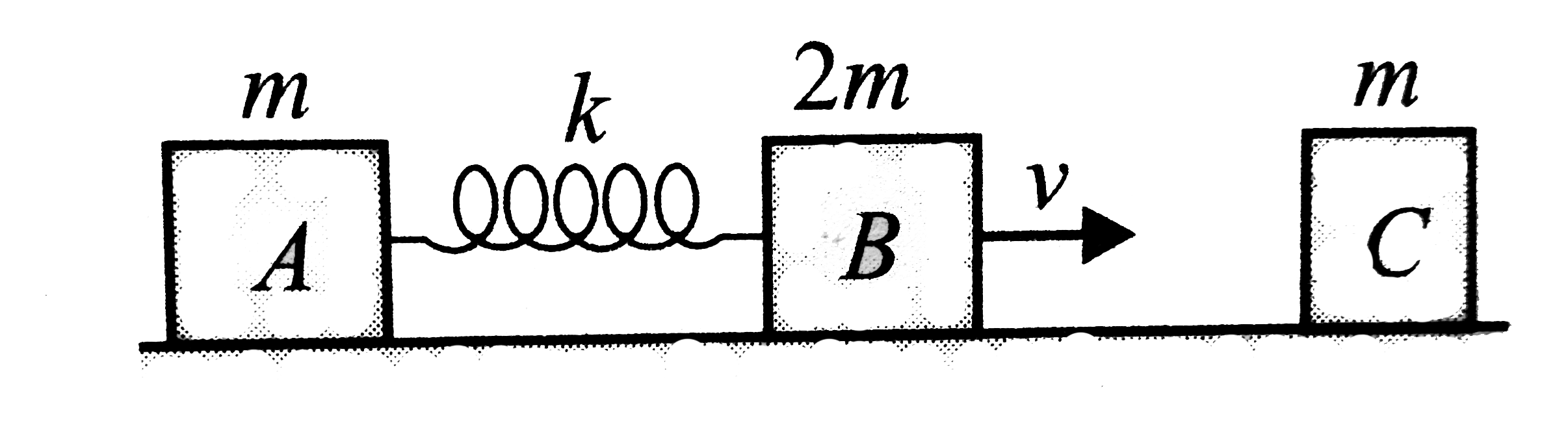
The correct Answer is:x=√mv212k
First considering an inelastic collision between B and C.
2mv(m+2m)vB
vB=23v velocity of (B and C)
Then velocity of centre of mass during maximum compression
vCM=3mv4m=34v

12mv24+123mv2(b+c)=124mv2CM+12kx2
Then substituting the value x=√mv212k
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Single Correct
Explore 141 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Exercise 1.3
Explore 24 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
An object initially at rest explodes into three equal fragments A,B and C.The momentum of A is pˆi and that of B is √3pˆj
where p is a+ve number. The momentum of C will be
View SolutionA ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
View SolutionA ball is dropped on a floor from a height h. If the coefficient of restitution is e, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionTwo blocks A and B of masses m and 2m , respectively are connected by a spring of force constant k . The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m , at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v_(0) each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m . at rest, the collision being completely inelastic. The velocity of block B just after collision is -
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
The velocity of centre of mass of system of block A, B, & C is -
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v_(0) each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m . at rest, the collision being completely inelastic. The maximum compression of the spring after collision is -
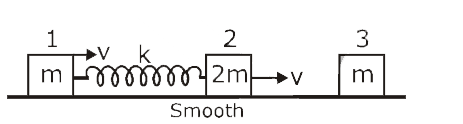
View SolutionTwo blocks 1 and 2 of masses m and 2m respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass, leading the lighter one. The spring is of natural length in the motion. Block 2 collides head on with a third block 3 of mass m, at rest, the collision being completely inelastic. Determine the velocity of blocks at the instant of maximum compression of the spring.
View Solutionm द्रव्यमान का एक ब्लॉक C,v0 वेग से चलता हुआ m द्रव्यमान के ब्लॉक A से टकराता है | ब्लॉक A, 2m द्रव्यमान के एक ब्लॉक B से k बल नियतांक की स्प्रिंग के द्वारा जुड़ा है | यदि A और B के वेग समान हैं तथा x0 स्प्रिंग का दबाव है, तो k का मान क्या है ?

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass, leading the lighter one. The spring is of natural length in the motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Determine the velocity of blocks at the instant of maximum compression of the spring.

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View Solution

