To find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
The correct Answer is:3
To solve the problem, we will follow these steps:
Step 1: Identify the variables and their dimensions
We know that the distance d depends on:
- Mass density of fog ρ
- Intensity of light S
- Frequency of light f
The dimensions of these variables are:
- Density ρ: (ρ)=ML−3
- Intensity S: Intensity is power per unit area, so (S)=PA=ML2T−3L2=ML0T−3
- Frequency f: (f)=T−1
Step 2: Write the relationship
According to the problem, we can express the distance d as:
d=k⋅ρa⋅Sb⋅fc
where k is a dimensionless constant.
Step 3: Write the dimensions of d
The dimension of distance d is:
(d)=L
Step 4: Substitute the dimensions into the equation
Substituting the dimensions into the equation gives:
L=(ML−3)a⋅(ML0T−3)b⋅(T−1)c
Step 5: Expand and simplify
Expanding this, we have:
L=Ma⋅L−3a⋅Mb⋅L0⋅T−3b⋅T−c
This simplifies to:
L=Ma+b⋅L−3a⋅T−3b−c
Step 6: Set up equations for each dimension
Now we can compare the dimensions on both sides:
1. For mass M: 0=a+b (Equation 1)
2. For length L: 1=−3a (Equation 2)
3. For time T: 0=−3b−c (Equation 3)
Step 7: Solve the equations
From Equation 2:
a=−13
Substituting a into Equation 1:
0=−13+b⟹b=13
Now substituting b into Equation 3:
0=−3⋅13−c⟹0=−1−c⟹c=−1
Step 8: Substitute values back
Now we have:
- a=−13
- b=13
- c=−1
Step 9: Relate S to n
The problem states that d is proportional to S1n. From our earlier work, we found that S has a power of 13:
S1n=S13
Thus, we can equate:
1n=13⟹n=3
Final Answer
The value of n is 3.
---
We know that the distance d depends on:
- Mass density of fog ρ
- Intensity of light S
- Frequency of light f
- Density ρ: (ρ)=ML−3
- Intensity S: Intensity is power per unit area, so (S)=PA=ML2T−3L2=ML0T−3
- Frequency f: (f)=T−1
According to the problem, we can express the distance d as:
d=k⋅ρa⋅Sb⋅fc
where k is a dimensionless constant.
The dimension of distance d is:
(d)=L
Substituting the dimensions into the equation gives:
L=(ML−3)a⋅(ML0T−3)b⋅(T−1)c
Expanding this, we have:
L=Ma⋅L−3a⋅Mb⋅L0⋅T−3b⋅T−c
This simplifies to:
L=Ma+b⋅L−3a⋅T−3b−c
Now we can compare the dimensions on both sides:
1. For mass M: 0=a+b (Equation 1)
2. For length L: 1=−3a (Equation 2)
3. For time T: 0=−3b−c (Equation 3)
From Equation 2:
a=−13
0=−13+b⟹b=13
0=−3⋅13−c⟹0=−1−c⟹c=−1
Now we have:
- a=−13
- b=13
- c=−1
The problem states that d is proportional to S1n. From our earlier work, we found that S has a power of 13:
S1n=S13
Thus, we can equate:
1n=13⟹n=3
The value of n is 3.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple correct Answer Type
8 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A glass wedge with a small angle of refraction θ is placed at a certain distance from a converging lens with a focal length f ,one surface of the wedge being perpendicular to the optical axis of the lens. A point sources S of light is on the other side of the lens at its focus. The rays reflected from the wedge (not from base) produce, after refraction in the lens , two images of the source displaced with respect to each other by d. Find the refractive index of the wedge glass. [Consider only paraxial rays.]
_E01_162_Q01.png)
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
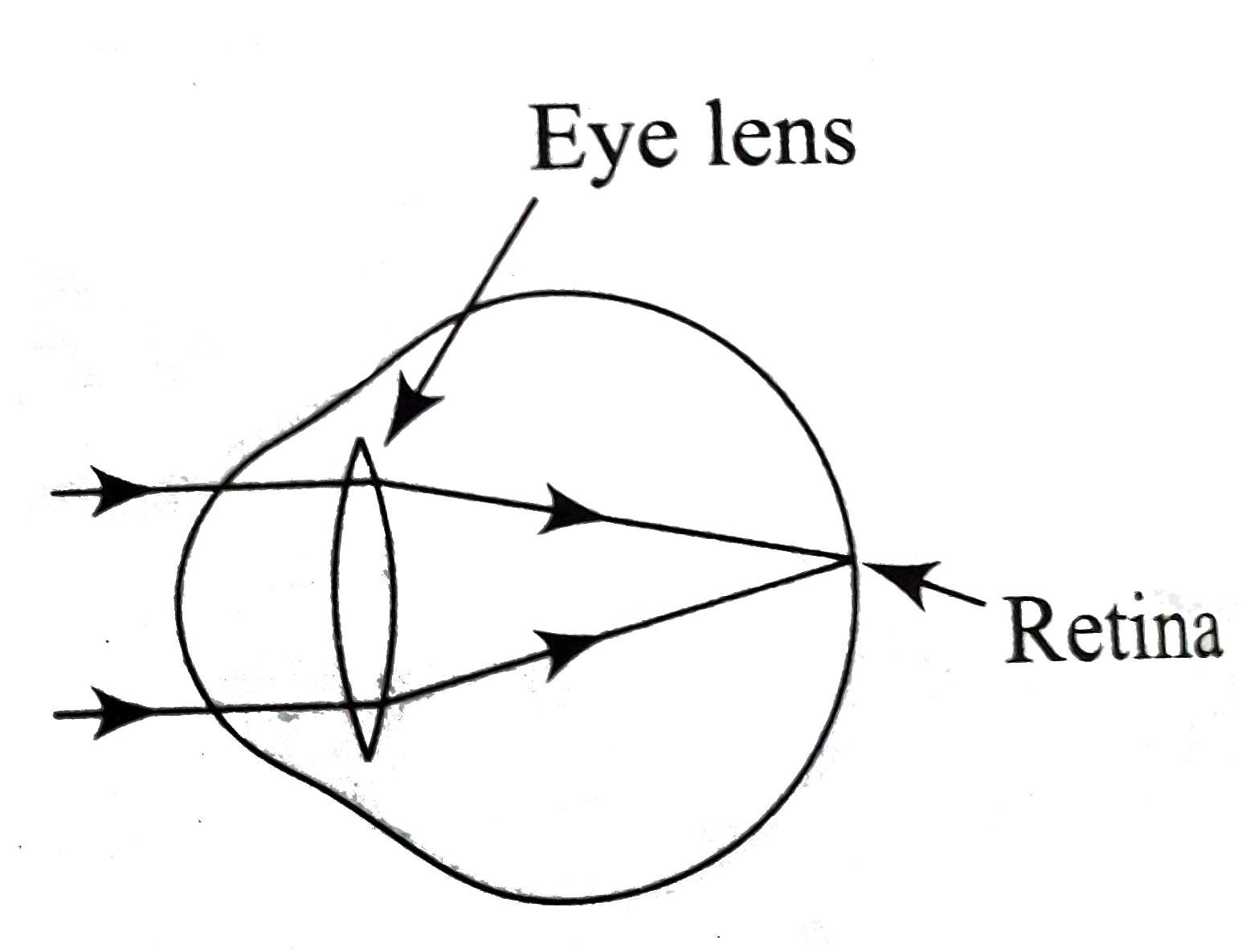
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
View Solution
Knowledge Check
To find the distance d over which a signal can be seen clearly in foggy conditions, a railways engineer uses dimensional analysis and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. The engineer finds that d is proportional to S1/n. The value of n is.
A4B2C3D1
The ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
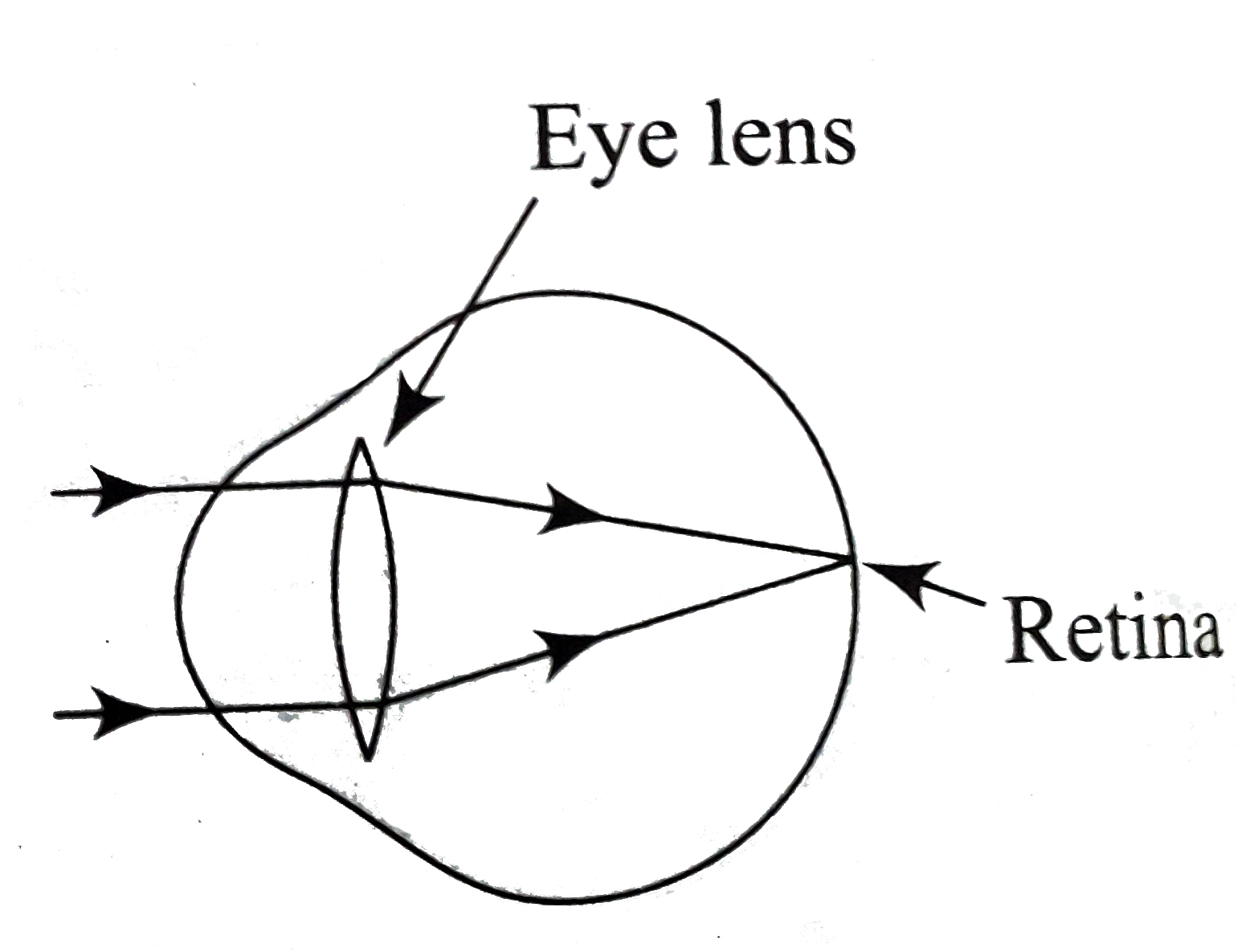
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
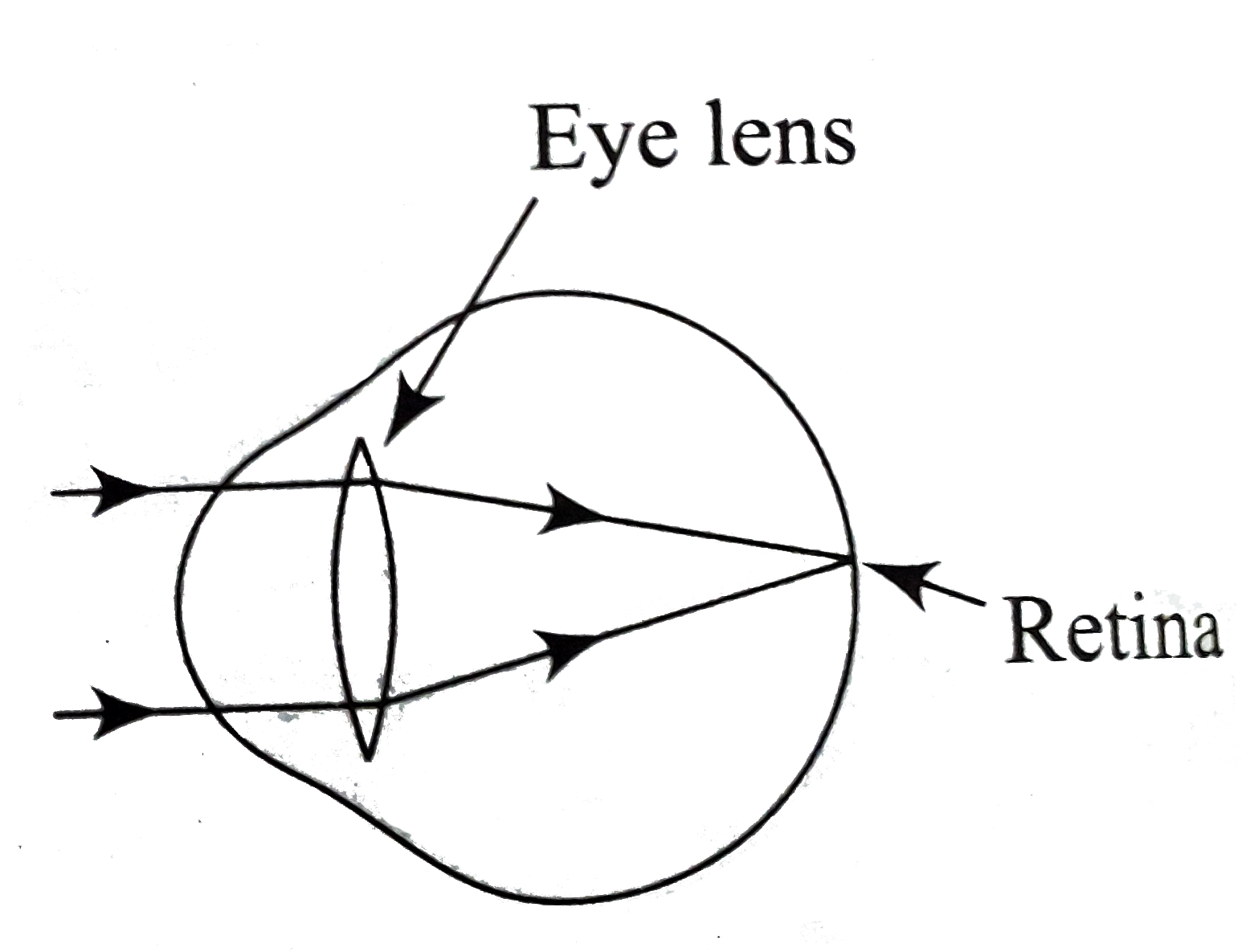
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
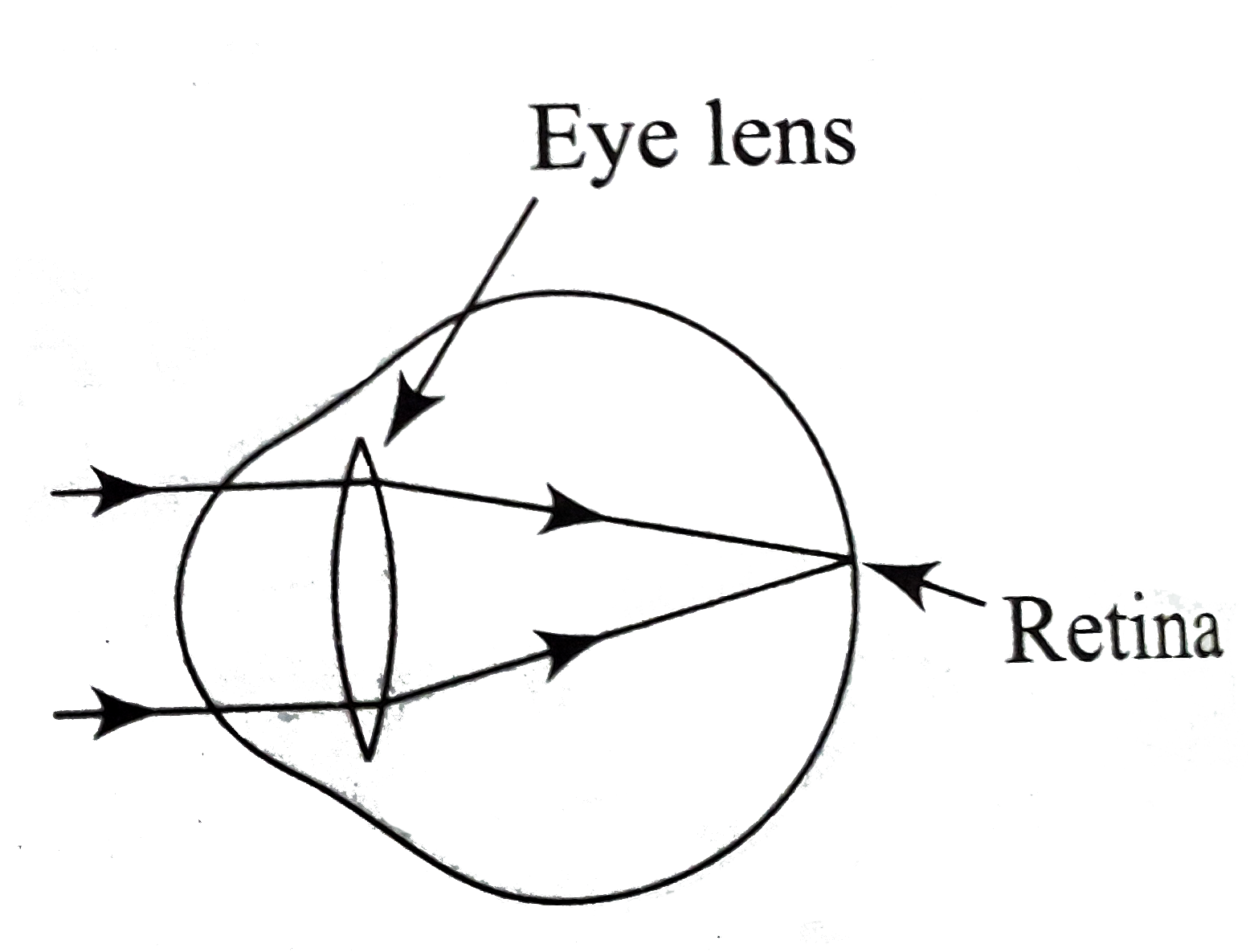
Q. Minimum focal length of eye lens of a normal peson is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
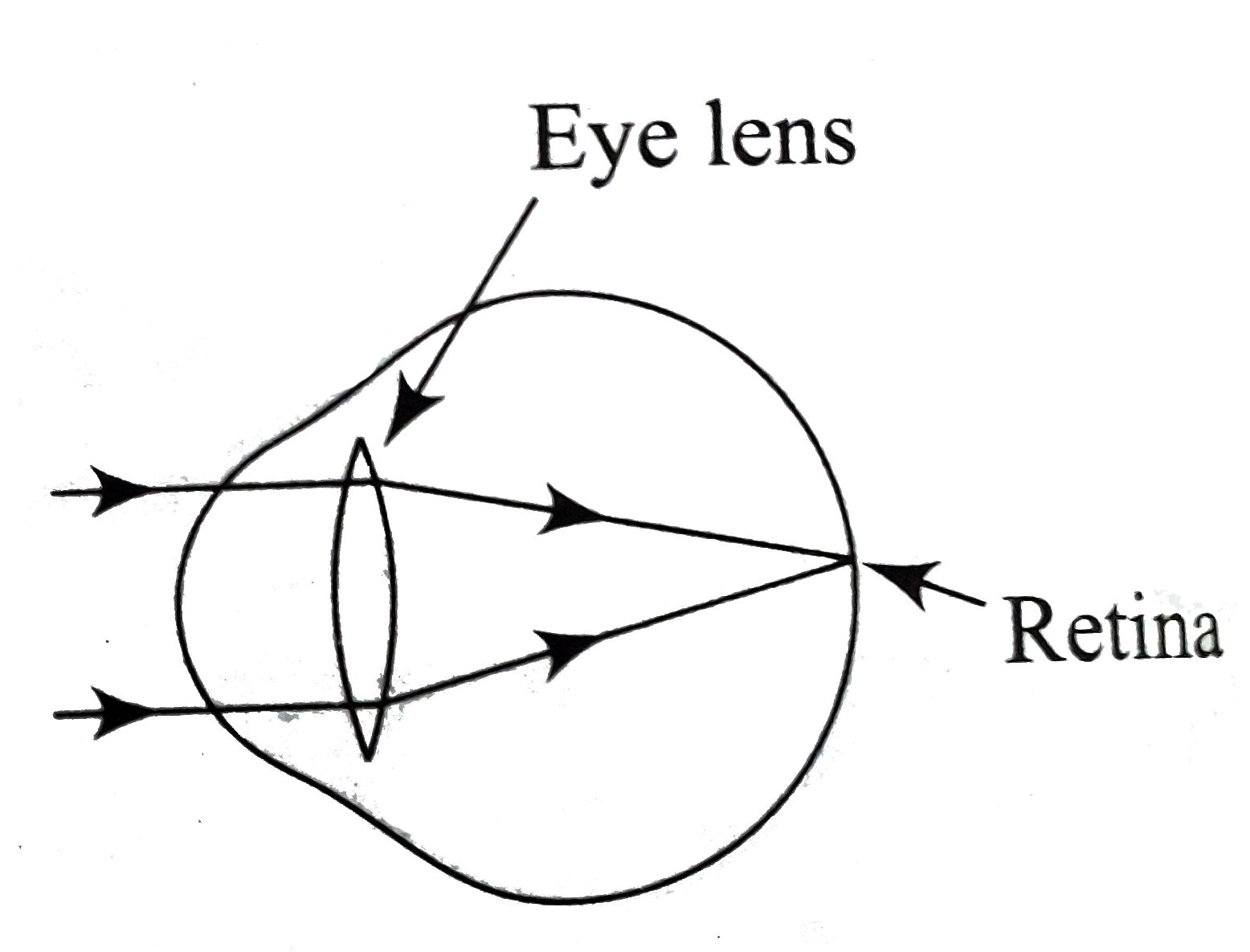
Q. Maximum focal length of a eye lens of a normal person is
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
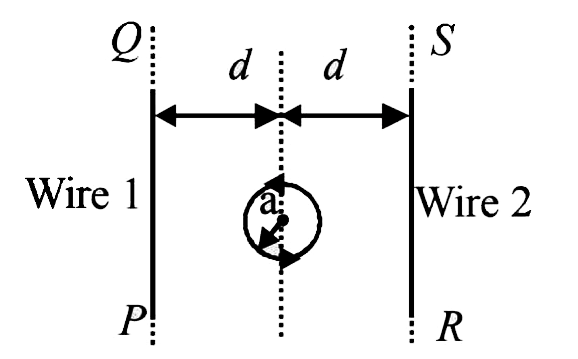
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View SolutionLet us assume that the de-Broglie wave asssociated with an electron froms a standing wave between the atoms arranged in a one-dimensional array with nodes at each of the atomic sites. If is found that one such standing wave is formed, if the distance between the atoms of the array is 3Å. A similar standing wave is again formed, if d is increased to 3.5Å but not for any intermediate value of d. Find the energy of the electrons in electron volts and the least value of d for which the standing wave of the type described above can from.
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View Solution
