Two identical blocks $A$ and $B$ , each of mass $m$ resting on smooth floor are connected by a light spring of natural length $L$ and spring constant $k$ , with the spring at its natural length. A third identical block $C$ (mass $m$ ) moving with a speed $v$ along the line joining $A$ and $B$ collides with $A$ . The maximum compression in the spring is

$v \sqrt{\frac{m}{2 k}}$

$v \sqrt{\frac{v}{2 k}}$

$\sqrt{\frac{m v}{k}}$

$\frac{m v}{2 k}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

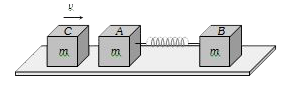
Initial momentum of the system (block C) = mv
After striking with A, the block C comes to rest and now both block A and B moves with velocity V, when compression in spring is maximum. By the law of conservation of linear momentum
$m v = (m + m) V \Rightarrow V = \frac{v}{2}$
By the law of conservation of energy
K.E. of block C = K.E. of system + P.E. of system
$\frac{1}{2} m v^{2} = \frac{1}{2} (2 m) V^{2} + \frac{1}{2} k x^{2}$
$\Rightarrow \frac{1}{2} m v^{2} = \frac{1}{2} (2 m) {(\frac{v}{2})}^{2} + \frac{1}{2} k x^{2}$
$\Rightarrow k x^{2} = \frac{1}{2} m v^{2}$
$\Rightarrow x = v \sqrt{\frac{m}{2 k}}$

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One or More
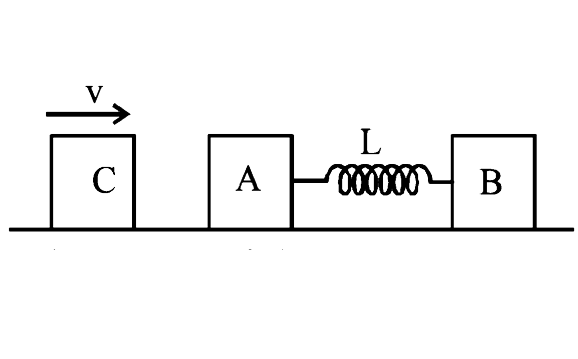
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then

Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.
Bthe kinetic energy of the A-B system, at maximum compression of the spring, is $m v^{2} / 4$ .
Cthe maximum compression of the spring is $v \sqrt{(m / K)}$
Dthe maximum compression of the spring is $v \sqrt{(m / 2 K)}$
Question 2 - Select One or More
Two blocks $A$ and $H$ . each of mass $m$ , are connected by a massless spring of natural length $I$ . and spring constant $K$ . The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block $C$ , also of mass $m$ , moves on the floor with a speed $v$ along the line joining $A$ and $B$ . and collides elastically with $A$ . Then

Athe kinetic energy of the $A - B$ system, at maximum compression of the spring, is zero.
Bthe kinetic energy of the $A - B$ system, at maximum compression of the spring, is
Cthe maximum compression of the spring is $\sqrt{(\frac{m}{K})}$
Dthe maximum compression of the spring is $v \sqrt{(\frac{m}{2 K})}$
Question 3 - Select One
A block of mass m moving with velocity $v_{0}$ on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

A $\sqrt{\frac{2 m}{k}} v_{0}$
B $\sqrt{\frac{m}{k}} . v_{0}$
C $\sqrt{\frac{m}{k}} . v_{0}$
D $\frac{m}{2 k} . v_{0}$

ERRORLESS -WORK , ENERGY , POWER AND COLLISION-Ordinary Thinking (Objective Questions) (Conservation of Energy and Momentum)

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

ERRORLESS -WORK , ENERGY , POWER AND COLLISION-Ordinary Thinking (Objective Questions) (Conservation of Energy and Momentum)

A block of mass m moving with velocity $v_{0}$ on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is