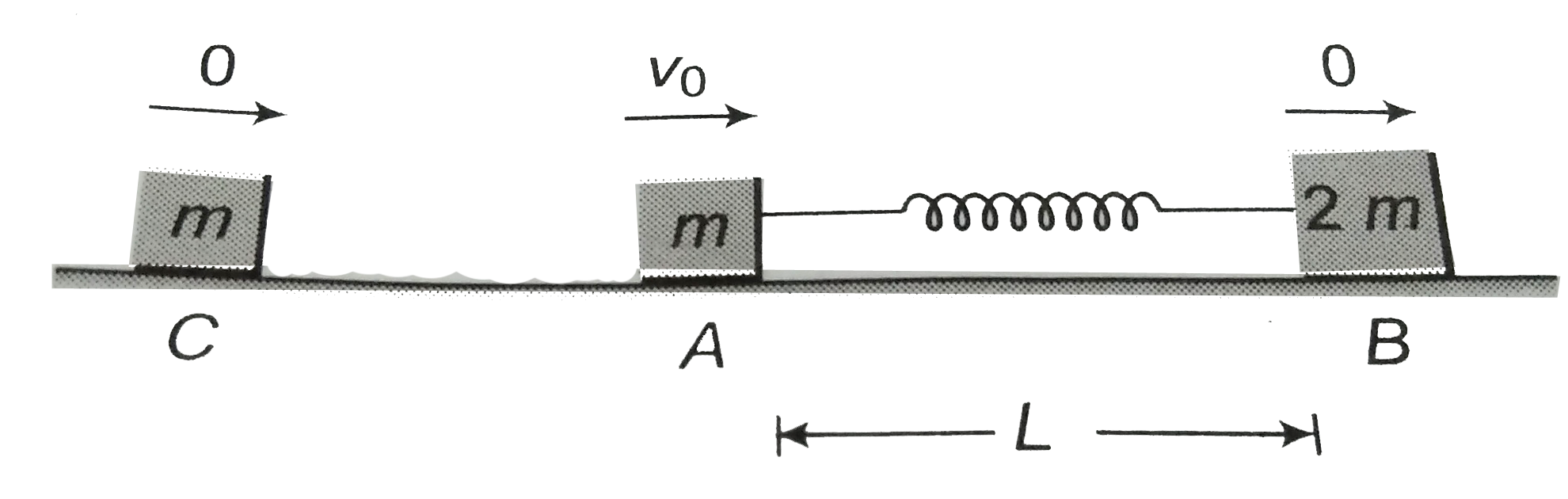
Two blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

Since the collision is head - on elastic , there will be exchange of velocity , block C comes to rest and block A acquires speed v0 towards right
vc.m.=mv0+2m×0m+2m=v03
Since the external force is zero , vc.m.=constant. As the blocks move , the spring will be compressed.
Due to the spring force , kx , the speed of m decreases and that of 2m increases , until the spring is compressed to maximum. At the time of maximum compression (or maximum elongation , to be shown in other problem) blocks will move with same velocity .
x0 : maximum compression of the spring
By the momentum conservation between (1) and (2)
mv0+2m×0=mv+2mv⇒v=v03
By the energy conservation between (1) and (2)
12mv20=12mv2+12×2mv2+12kx20
=12×3m(v03)2+12kx20
mv20=mv203+kx20
x0=√2mv203k=v0√2m3k


Topper's Solved these Questions
Similar Questions
Two blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View Solution
Knowledge Check
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
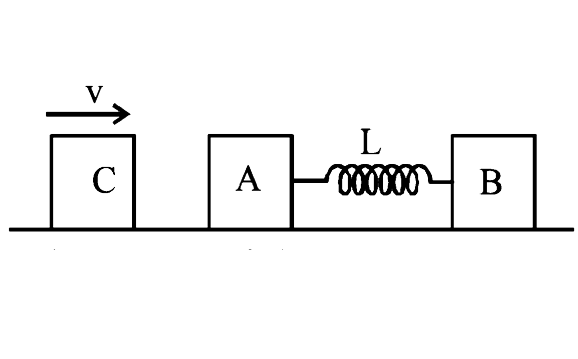 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)Two blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)
Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2k
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
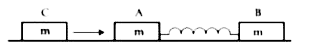
View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View Solution

