A block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
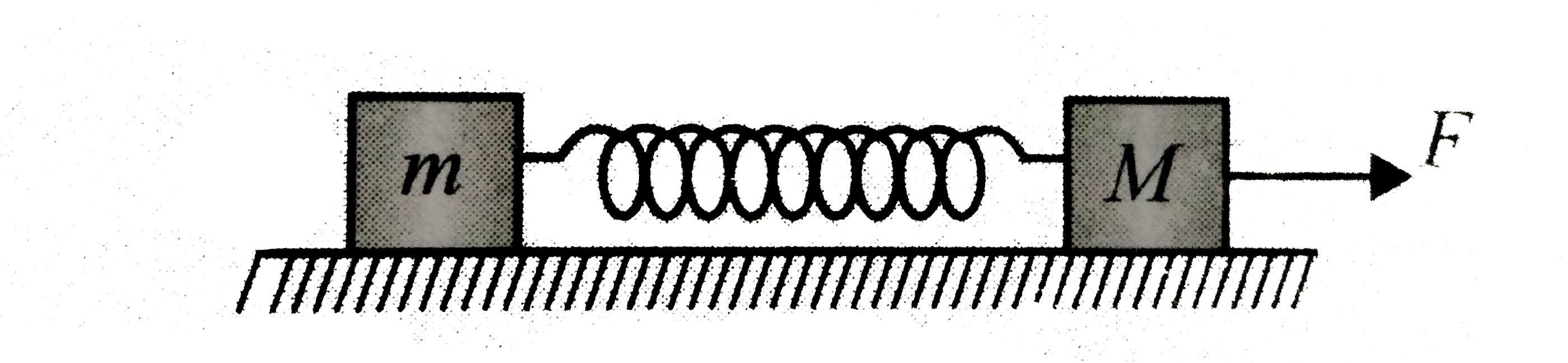
We solve the situation in the reference frame of centre of mass As only F is the external force acting on the system, due to this force, the acceleration of the centre of mass is FM+m. Thus, with respect to centre of mass, there is as pseudoforce on the two mases in the opposite direction,the free body digram of m and M with respect to centre of mass (taking centre of mass at rest) is shown in figure.
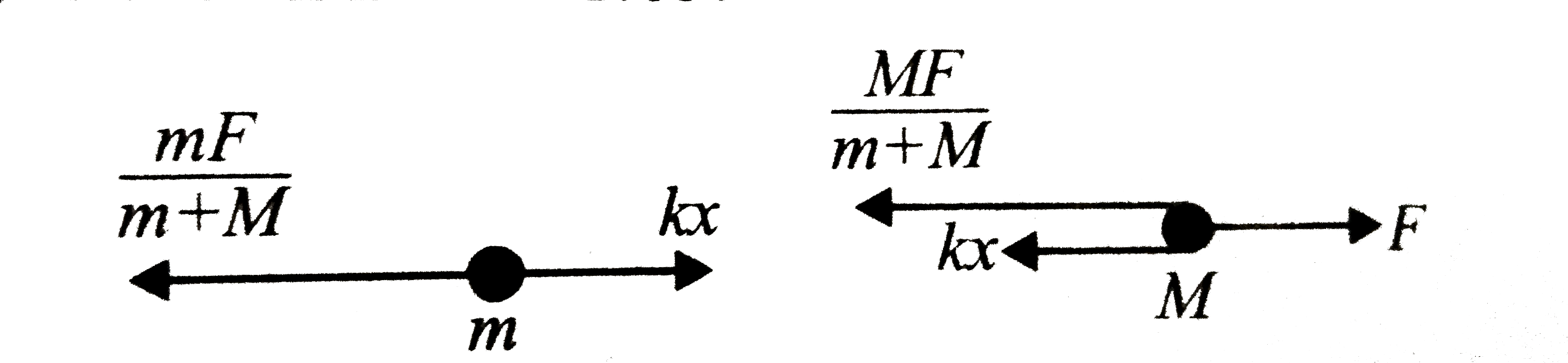
Taking centre of mass ast rest, if m moves maximum by a distance x1 and M moves maximum by a distance x2 then the work done by external forces (including pseudoforce) will be
W=mFm+Mx1+(F−MFm+M)x2=mFm+M(x1+x2)
this work is stored in the form of potential energy of the spring as U=(12)k(x1+x2)2.
Thus, on equation we get the maximum extension in the spring, as after this instant the sprig starts contracting.
12k(x1+x2)2=mFm+M(x1+x2)
⇒xmax=x1+x2=2mFk(m+M)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
Knowledge Check
A block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
A(a) MF(m+M)B(b) mFMC(c) (M+m)FmD(d) mF(m+M)A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
A block of mass m is connected to another block of mass M by a massless spring of spring constant K. Blocks are kept on a smooth horizontal plane. Initally both the blocks the at rest and spring is unstressed. Force F is applied on M to right as shownin the figure then which of the following is correct ?

View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
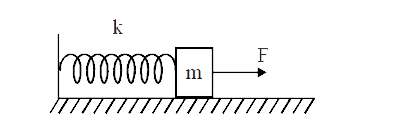
maximum extension in the spring
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
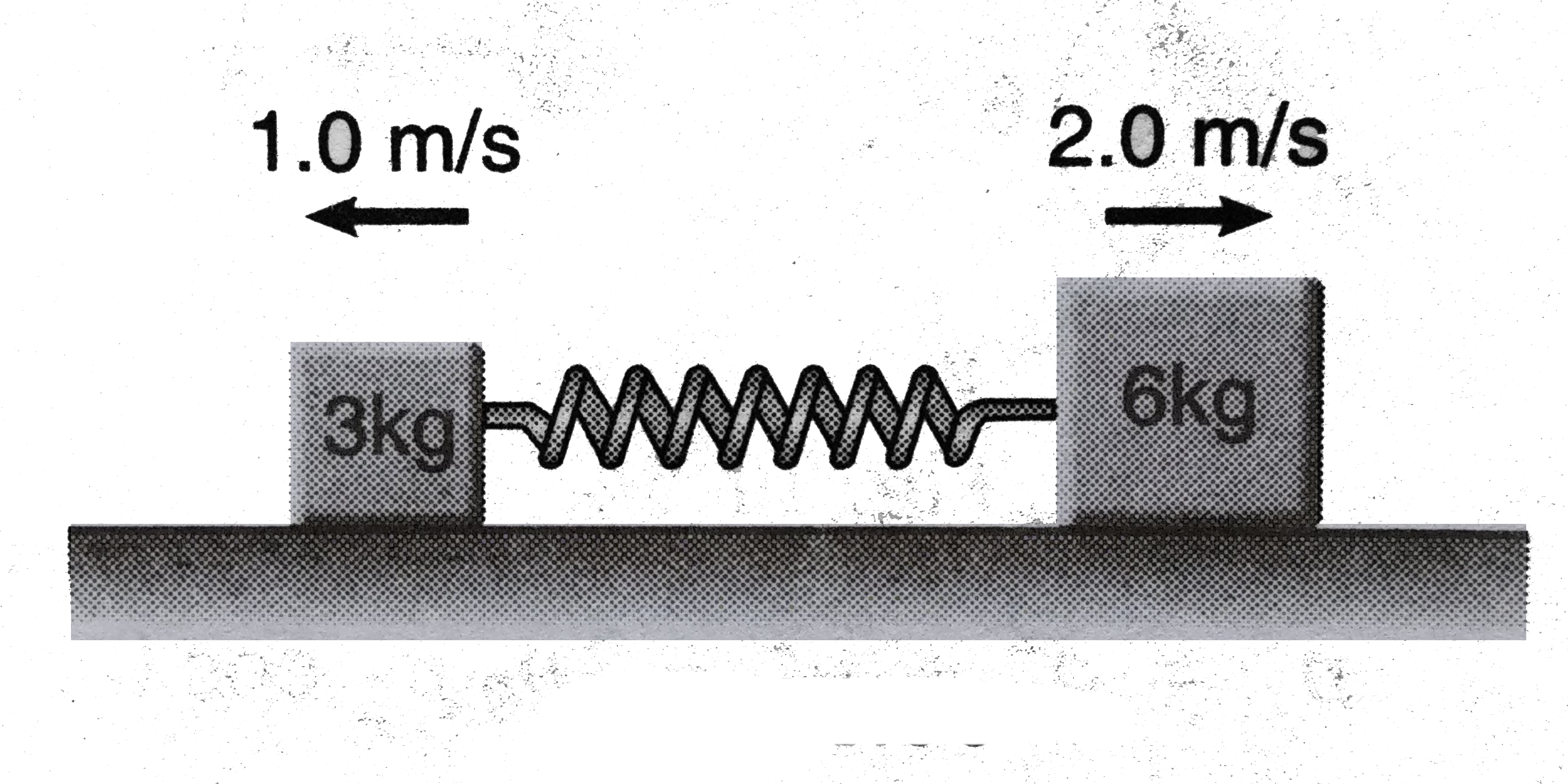
View SolutionTwo blocks connected by a spring rest on a smooth ITIM horizontal plane as shown in figure. A constant force F starts acting on block m2 as shown in the figure. Which of the following statements are not correct?

View Solution
