Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
v√m2k
m√m2k
√mvk
mv2k
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have three blocks: A and B are at rest and connected by a spring, while block C is moving towards block A with speed v. The goal is to find the maximum compression x of the spring when block C collides with block A.
Step 2: Apply Conservation of Momentum
Since there are no external forces acting on the system, we can conserve momentum. The initial momentum of the system is given by the momentum of block C, as blocks A and B are at rest.
Initial momentum:
pinitial=mv
After the collision, let the velocity of blocks A and B (which will be the same at maximum compression) be V. The total mass of the system after the collision is 2m (mass of A and B).
Final momentum:
pfinal=mv+mv=2mV
Setting initial and final momentum equal gives:
mv=2mV⟹V=v2
Step 3: Apply Conservation of Energy
At maximum compression of the spring, the kinetic energy of the system will be converted into potential energy stored in the spring.
Initial kinetic energy (only block C is moving):
KEinitial=12mv2
Final kinetic energy (both blocks A and B are moving with velocity v2):
KEfinal=12m(v2)2+12m(v2)2=12m(v24)+12m(v24)=mv24
The potential energy stored in the spring at maximum compression x is given by:
PE=12kx2
Step 4: Set Up the Energy Conservation Equation
The loss in kinetic energy equals the potential energy stored in the spring:
KEinitial−KEfinal=PE
12mv2−mv24=12kx2
Step 5: Simplify the Equation
Calculating the left side:
12mv2−mv24=2mv24−mv24=mv24
Setting this equal to the potential energy:
mv24=12kx2
Step 6: Solve for Maximum Compression x
Multiplying both sides by 2:
mv22=kx2
Rearranging gives:
x2=mv22k
Taking the square root:
x=√mv22k
Final Answer
The maximum compression in the spring is:
xmax=√mv22k
---
We have three blocks: A and B are at rest and connected by a spring, while block C is moving towards block A with speed v. The goal is to find the maximum compression x of the spring when block C collides with block A.
Since there are no external forces acting on the system, we can conserve momentum. The initial momentum of the system is given by the momentum of block C, as blocks A and B are at rest.
pinitial=mv
pfinal=mv+mv=2mV
mv=2mV⟹V=v2
At maximum compression of the spring, the kinetic energy of the system will be converted into potential energy stored in the spring.
KEinitial=12mv2
KEfinal=12m(v2)2+12m(v2)2=12m(v24)+12m(v24)=mv24
PE=12kx2
The loss in kinetic energy equals the potential energy stored in the spring:
KEinitial−KEfinal=PE
12mv2−mv24=12kx2
Calculating the left side:
12mv2−mv24=2mv24−mv24=mv24
mv24=12kx2
Multiplying both sides by 2:
mv22=kx2
x2=mv22k
x=√mv22k
The maximum compression in the spring is:
xmax=√mv22k
Topper's Solved these Questions
Similar Questions
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View Solution
Knowledge Check
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
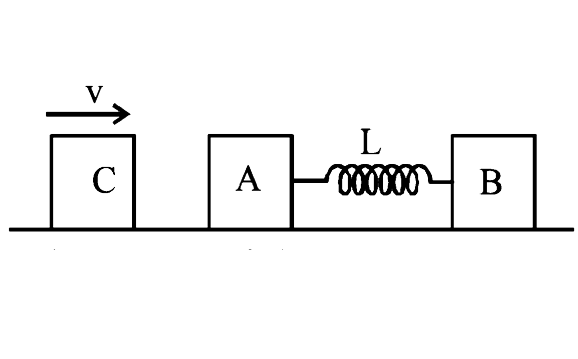 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)Two blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)
Athe kinetic energy of the A−B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A−B system, at maximum compression of the spring, isCthe maximum compression of the spring is √(mK)Dthe maximum compression of the spring is v√(m2K)A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
Two blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring

View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

View Solution

