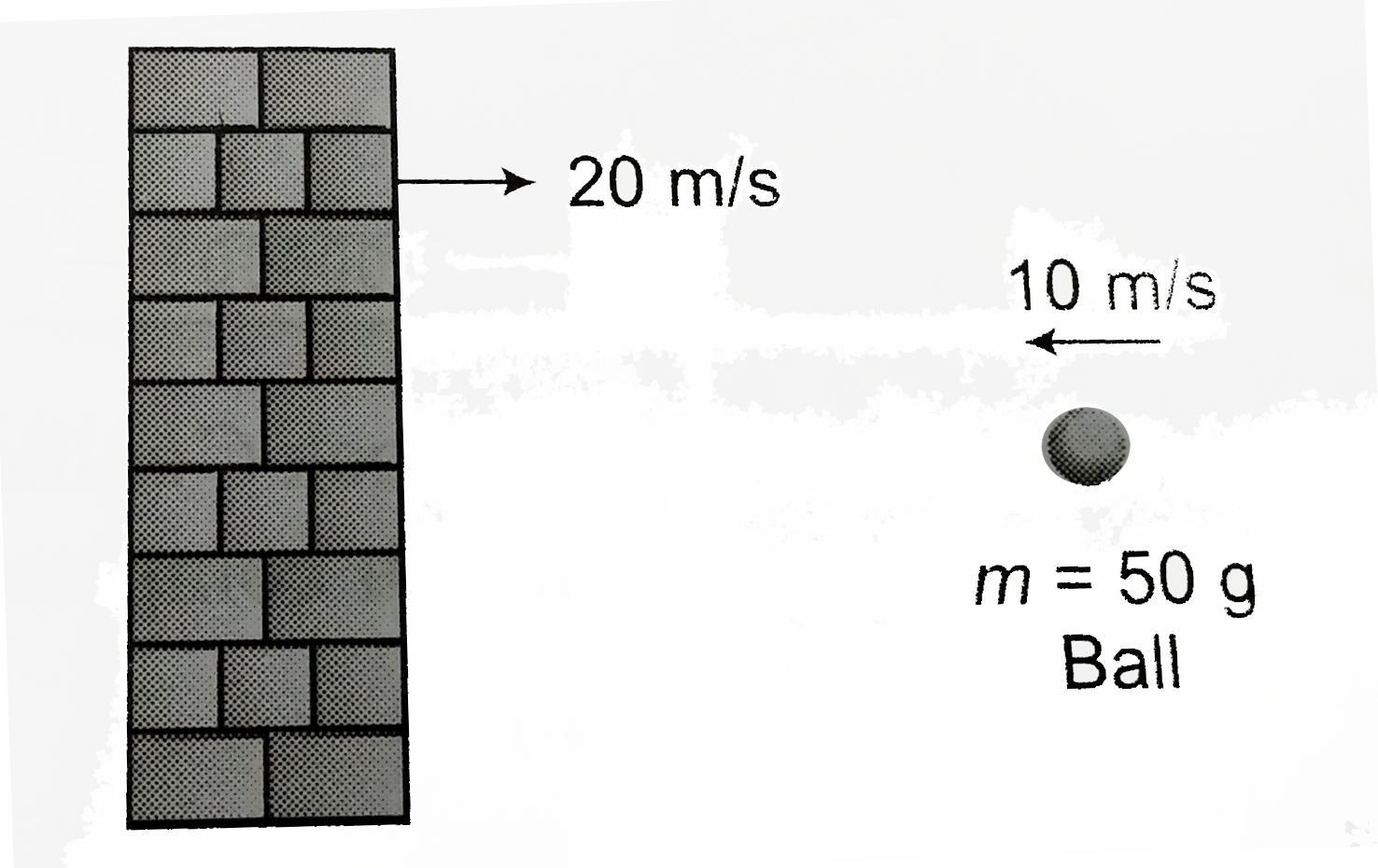
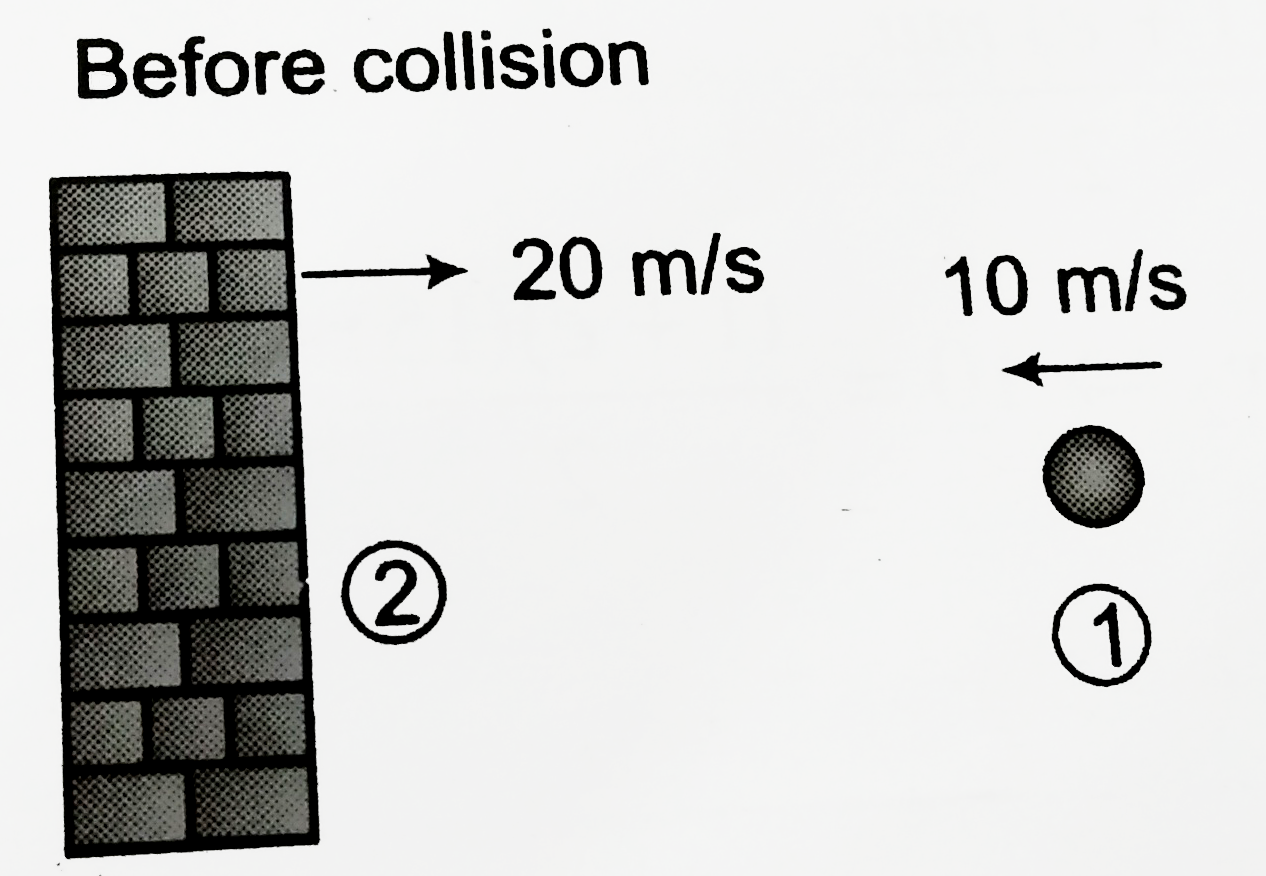
Consider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
30J
60J
90J
120J
The correct Answer is:B
Before collision
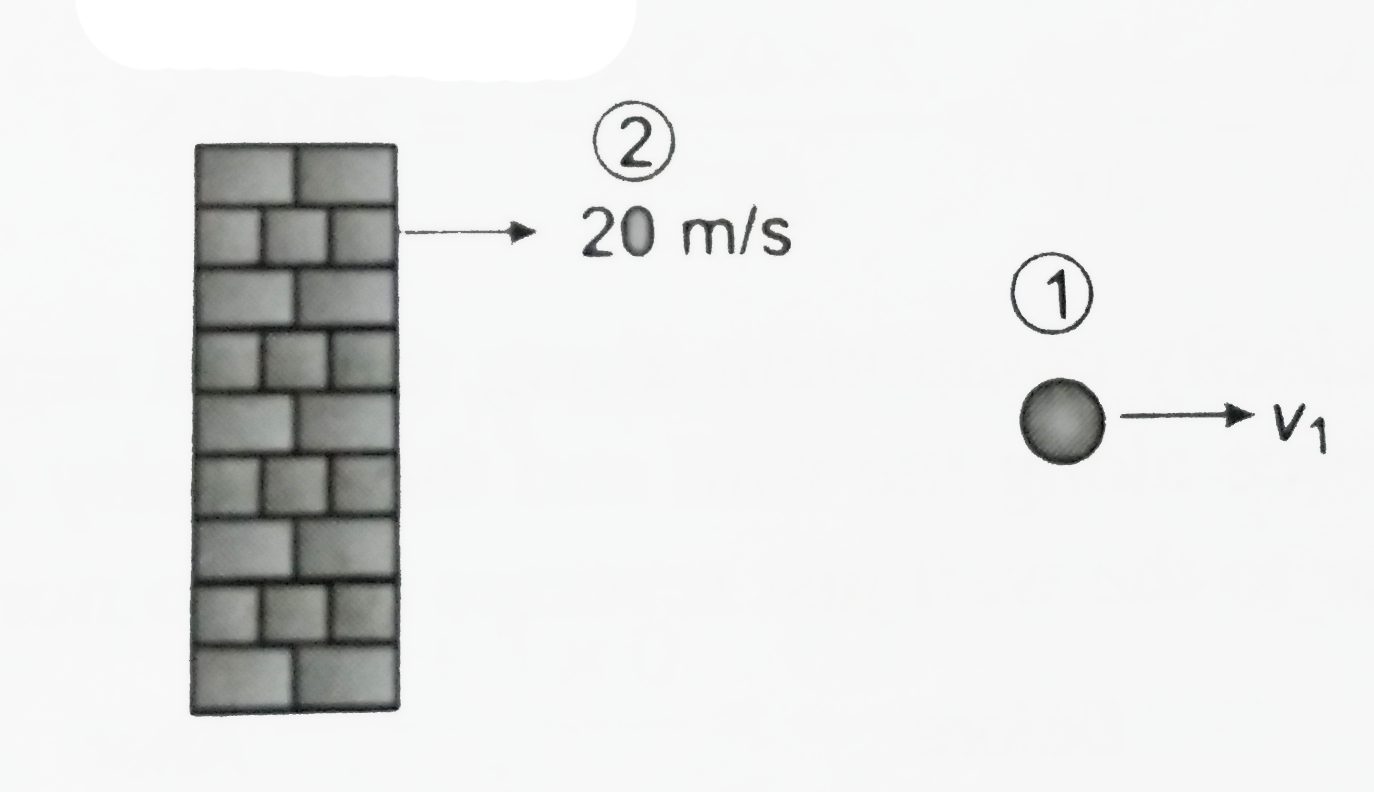
After collision
v1−v2=−e(u1−u2) , here e=1
v1−20=−1(−10−20)⇒v1=50m/s
For ball , ΔK=12m(v21−u21)
For ball , ΔK=12m(v21−u21)
=12×50×10−3(502−102)=60J
Topper's Solved these Questions
Similar Questions
A ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
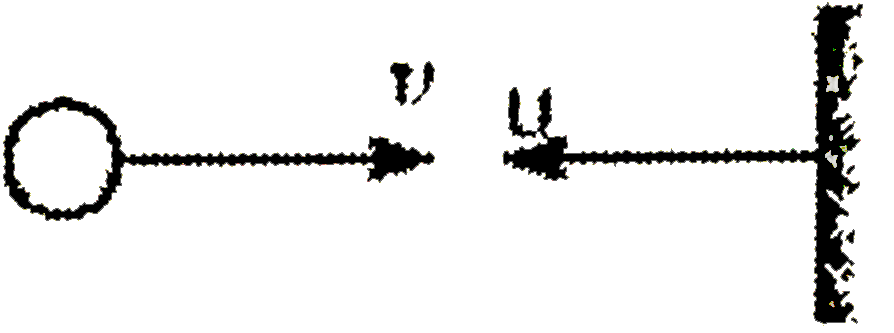
View SolutionConsider the situation as shown.
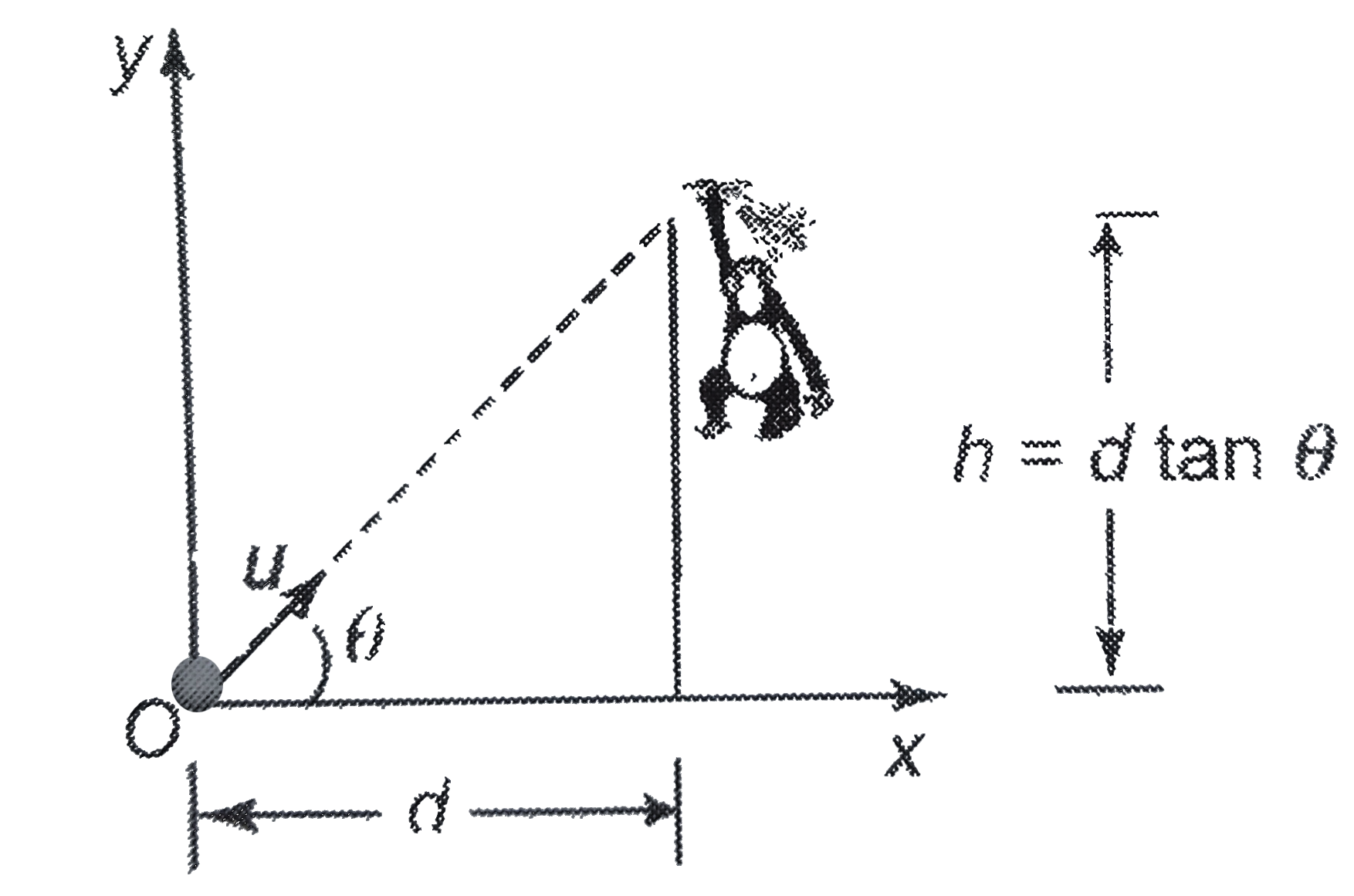
When a ball is thrown aiming the monkey, at the same time the monkey drops himself. Will the ball hit the monkey ?
View Solution
Knowledge Check
Two massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
A5 m s−1 to the rightB5 m s−1 to the leftC1 m s−1 to the rightD1 m s−1 to the leftTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
A5ms−1 to the rightB5ms−1 to the leftC1ms−1 to the rightD1ms−1 to the leftWe know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.
The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls A,B, and C are projected from ground with same speed at same angle with the horizontal. The ball A,B and C collide with the wall during their flight in air and all three collide perpendicularly with the wall as shown in figure.
The vertical component of velocity of balls wiht which they are projected isA20m/sB10m/sC10√3m/sDUndeterminable
A small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
View SolutionA steel ball weighting 1 kg is fastened to a cord 1 m long and is released when the cord is horizontal . At the bottom of its path the ball strikes a 5-kg steel block initially at rest on a frictionless surface . The collision is elastic . Find the speed of the ball and speed of the block just after collision . (g = 9.8ms−2)
[Hint : Apply principal of conservation of momentum and conservation of kinetic energy as the collision is elastic .]
View SolutionA smooth ball hits a smooth wall at a certain angle. The collision is elastic. Prove that the angle of reflection is equal to the angle of incidence.
View Solutionn bullets per sec each of mass m moving with velocity v strike normally on a wall. The collision is elastic then force on wall is-
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.
After the first collision, what is the total loss in kinetic energy of the balls?
View Solution