The ball sticks to block C, then block Ccollides elastically , head - on with A. If the maximum compression is x0, the spring constant k is
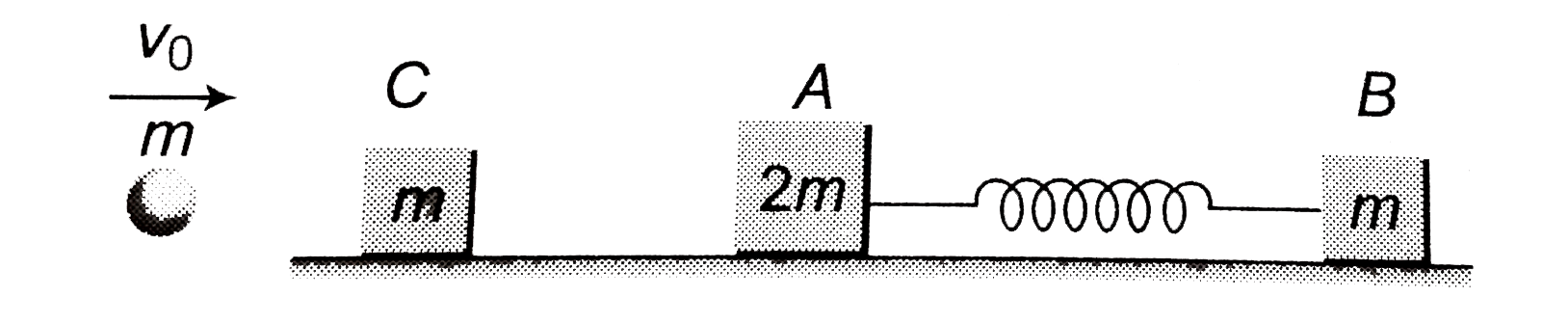
23mv20x20
mv202x20
mv203x20
mv206x20
The correct Answer is:D
When a ball sticks to block C , the common velocity is
mv0+m×0=(m+m)v⇒v=v02
Now after the head - on elastic collision , block C stops and A acquires velocity v0/2.
At the maximum compression , the blocks move together.
2mv02+m×0=2mv'+mv'⇒v'=v03
12.2m(v02)2=12(2m+m)v'2+12kx20
k=mv206x20
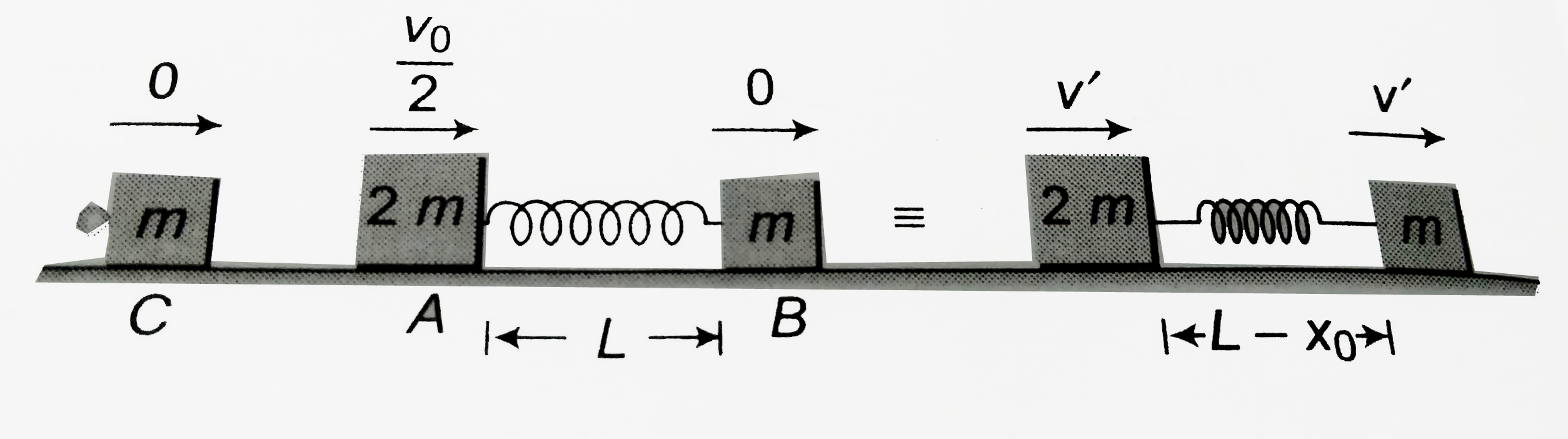
Topper's Solved these Questions
Similar Questions
Knowledge Check
If blocks collide elastically head - on , the ratio of maximum compression of the left spring and the right spring will be
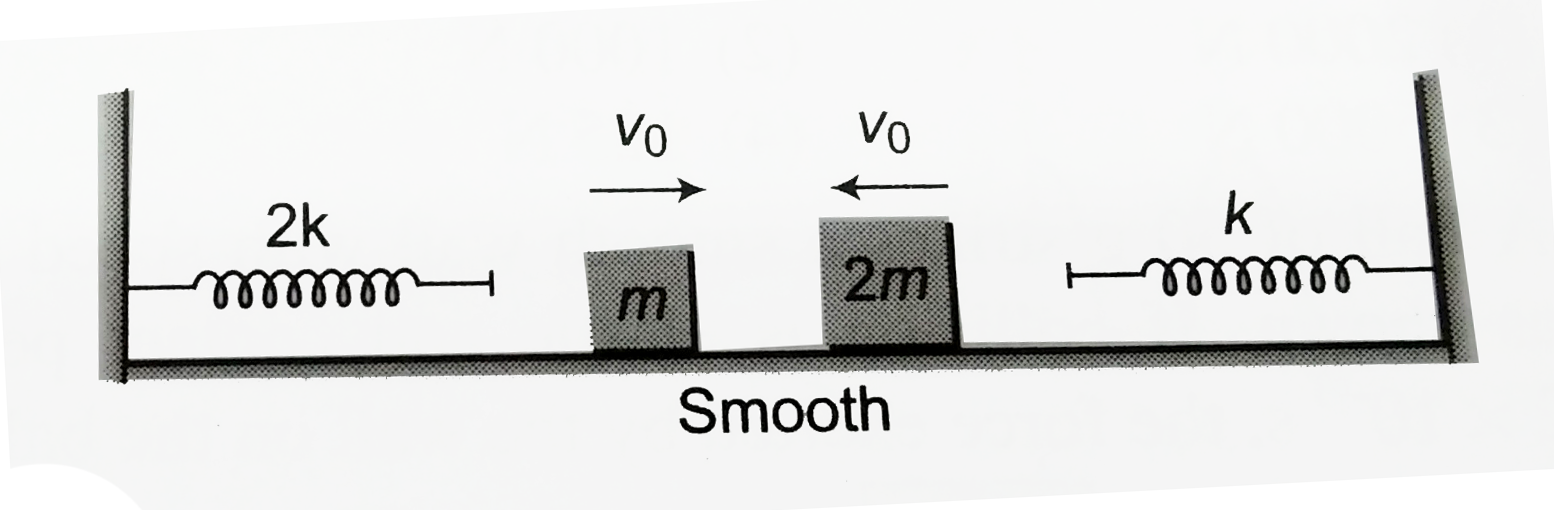 A3:5B2:3C5:4D5:2
A3:5B2:3C5:4D5:2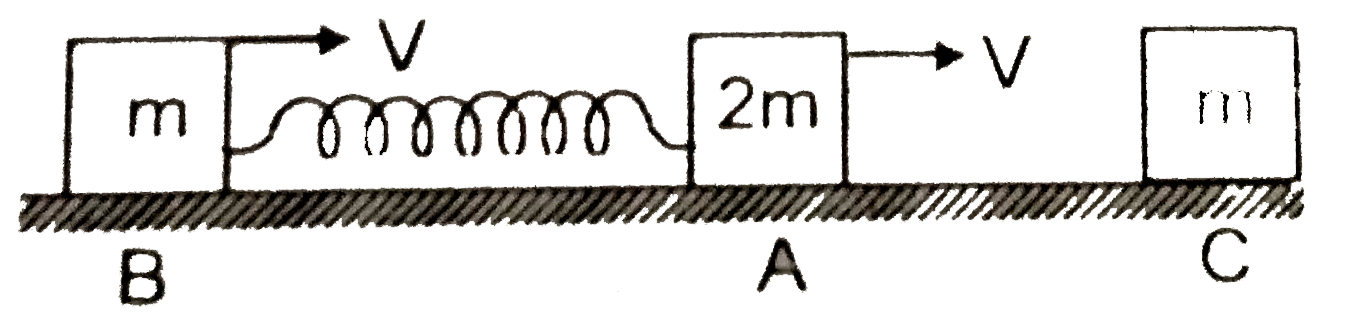
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will beA√32mkVB√27m8KVC√9m8KVD√8m27KVTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2k

In the figure, the spring is initially compressed by 3 cm and released. The block collides withth wall and rebounds to compress the spring again. The maximum compression in the srping after collision (coefficient of restitution is 0.7) is ........cm (Take √5=2.4,k=104Nm−1)
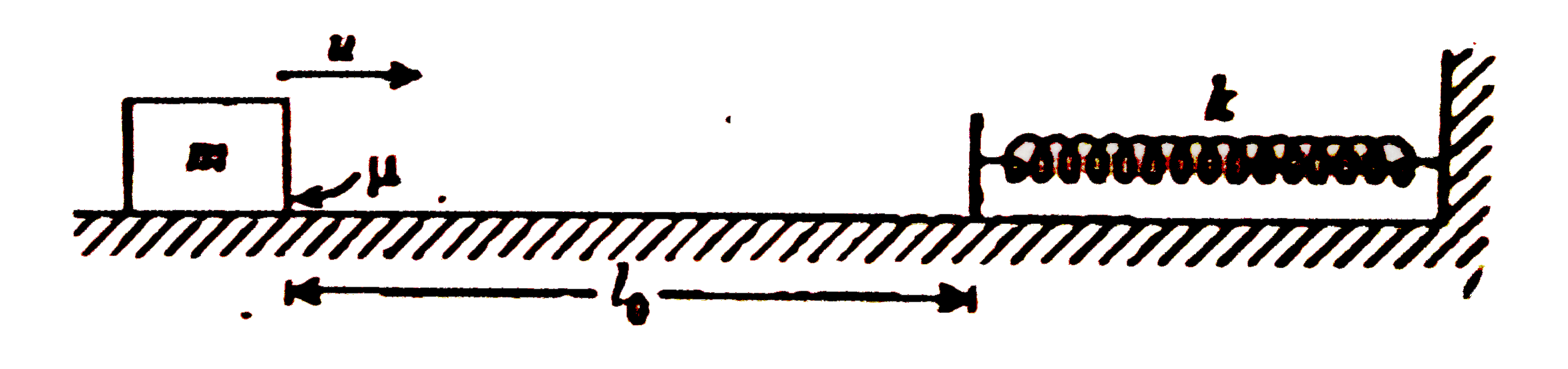
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
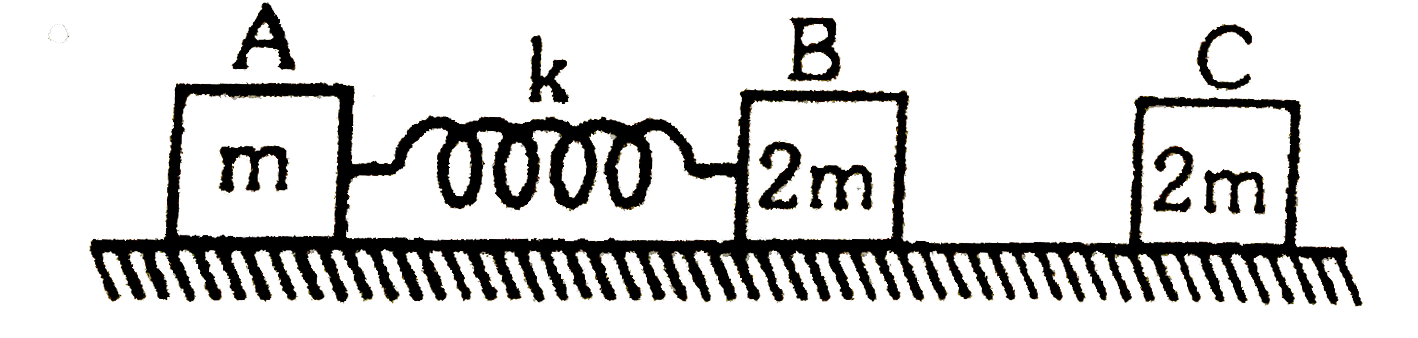
The maximum compression of the spring after collision is -
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
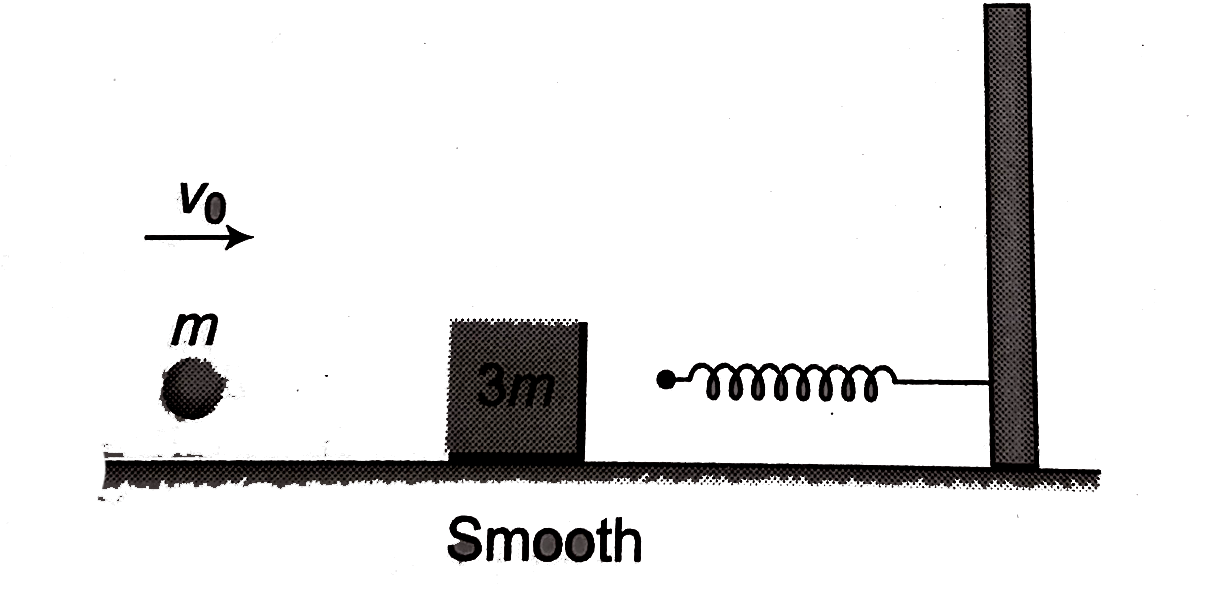
View Solution