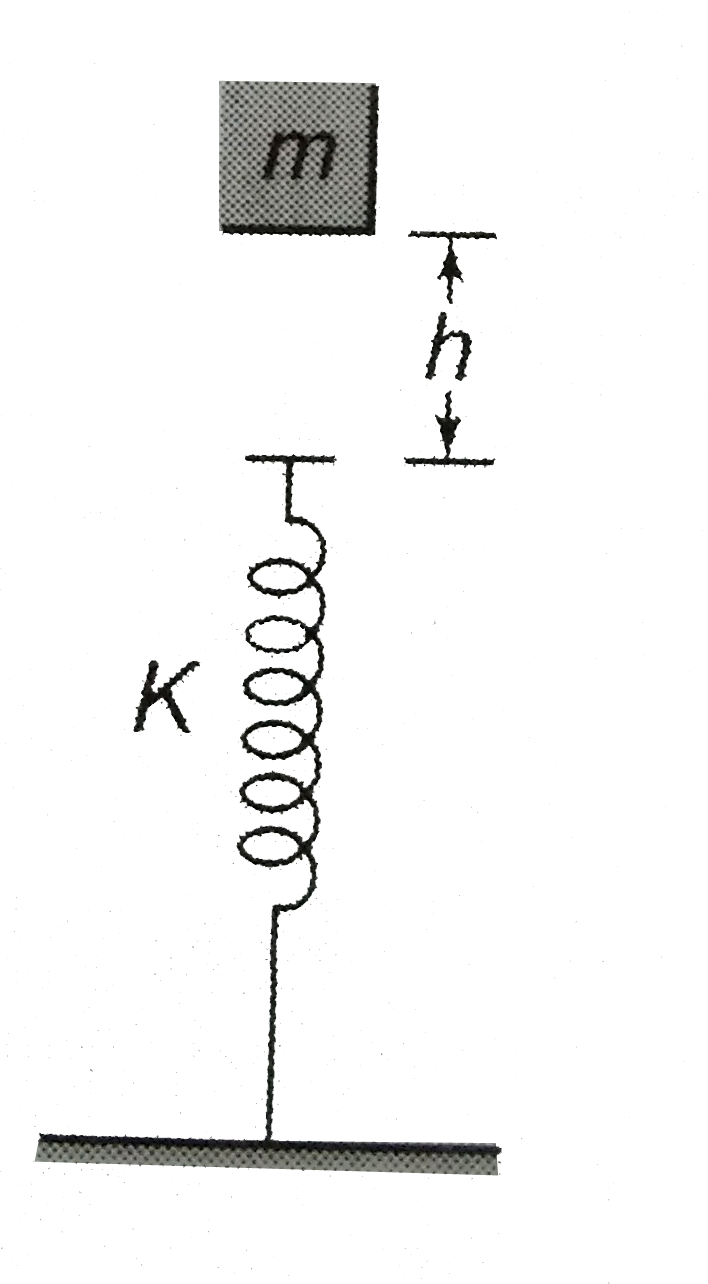
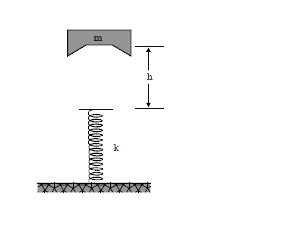
A block is released from height h, find the maximum compression of spring of spring constant k.
K1+Ug1+Us1=K2+Ug2+Us2
0+mg(h+x)+0=0+0+12kx2
kx2−2mgx−2mgh=0
x=−(−2)±√(−2mg)2−4k(−2mgh)2k
=mgk[1+√1+2khmg]
Maximum compression x=x0=mgk[1+√1+2khmg]
Topper's Solved these Questions
Similar Questions

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View SolutionA 700 g block is released from rest at height h0 above a vertical spring with spring constant k=450N/m and negligible mass. The block sticks to the spring and momentarily stops after compressing the spring 19.0 cm. How much work is done (a) by the block on the spring and (b) by the spring on the block ? (c) What is the value of h0 ? (d) If the block were released from height 2.00h0 above the spring, what would be the maximum compression of the spring ?
View Solution
Knowledge Check
A block of mass m is released from rest at point A. The compression in spring (force constant k) when the speed of block is maximum is found to be nmgcosθ4k. What should be the value of n?
 A2B3C4D1
A2B3C4D1A bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant (K) isA√MK(mucosθm)B√KM(MucosθM+m)C√MK(mucosθM+m)D√MK(mucosθM)A slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
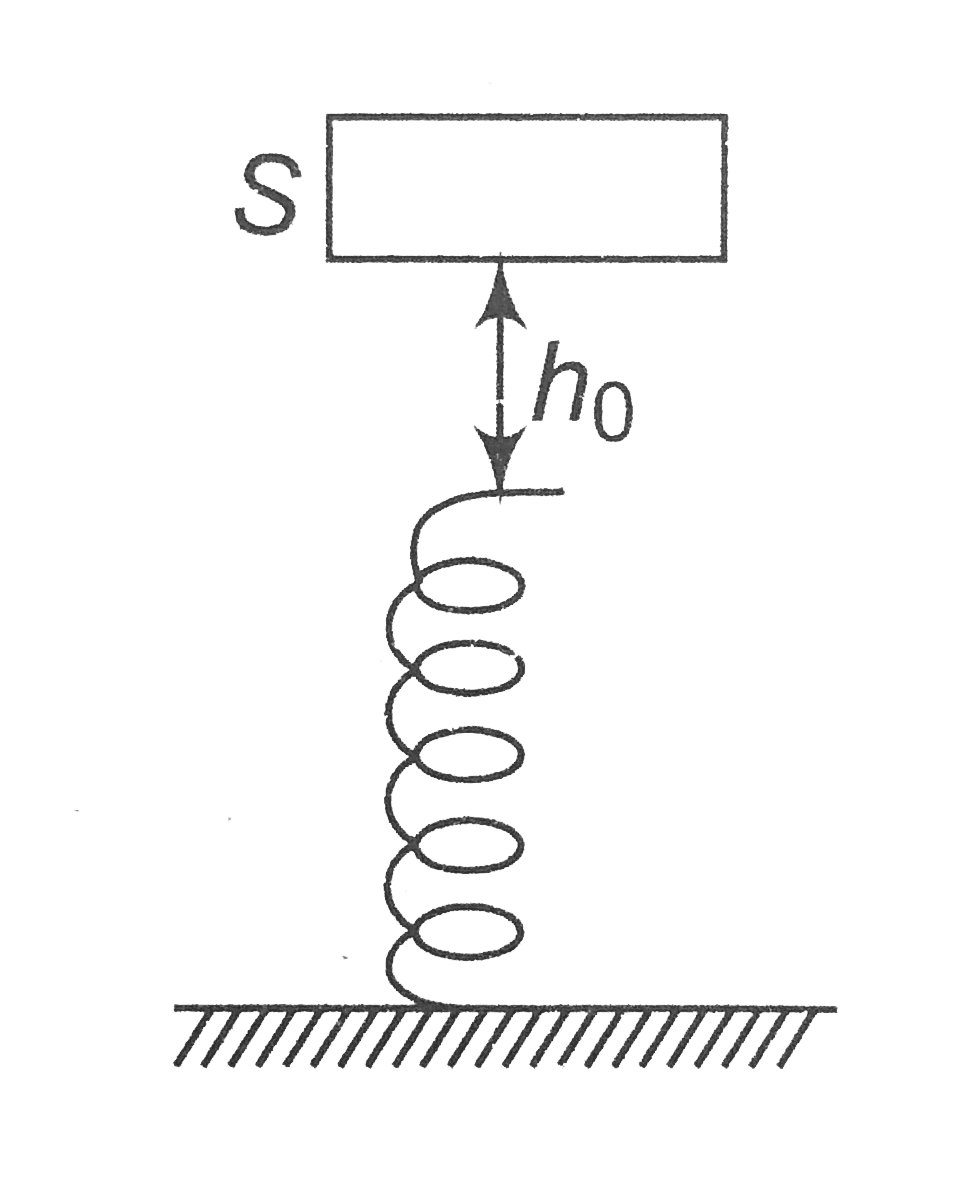 Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionA block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
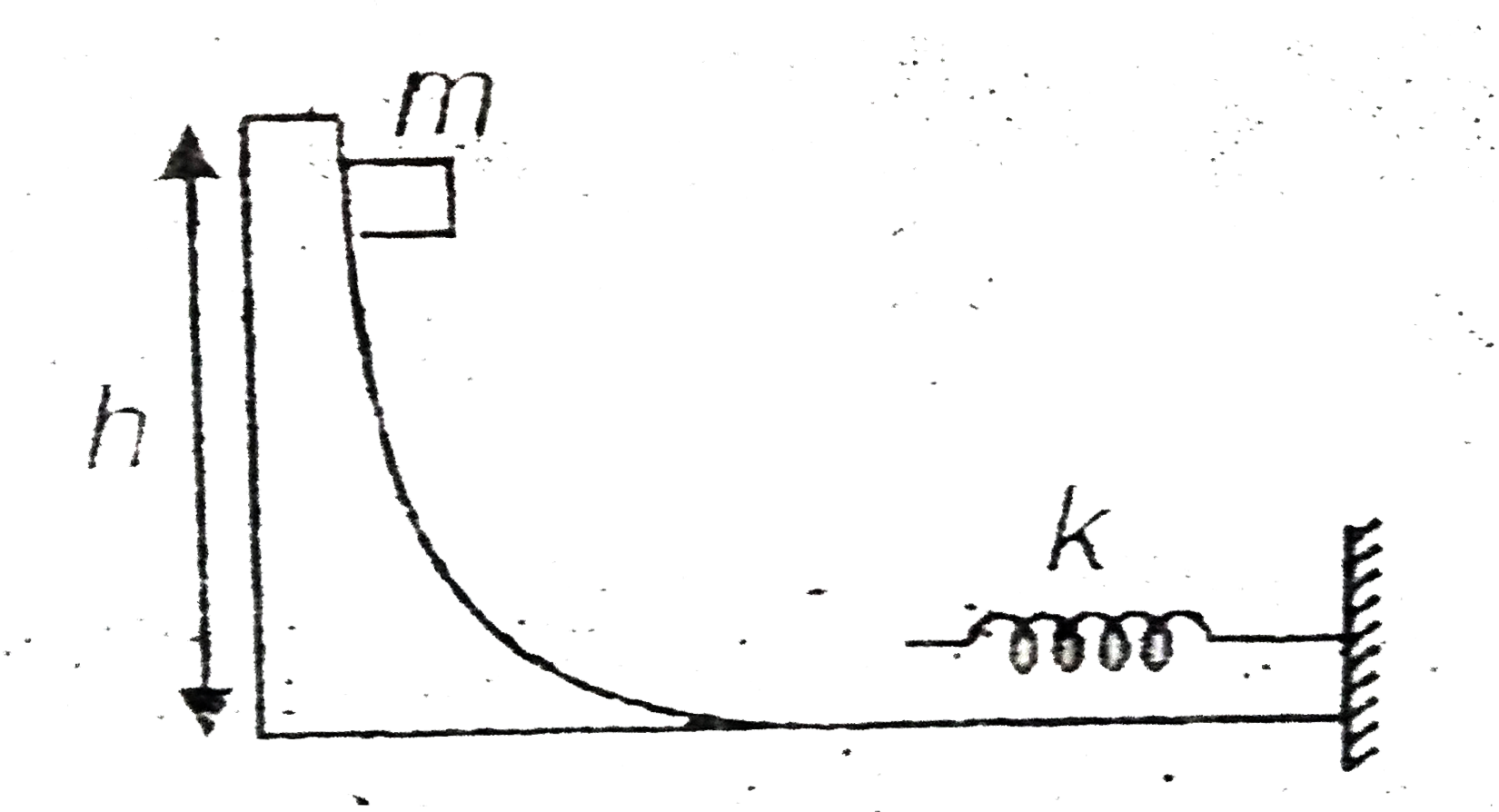
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View SolutionFind maximum compression is the spring from the given figure.

View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View Solution

