A particle is moving along the x-axis and force acting on it is given by $F = F_{0} {sin ω}_{x} N$ , where $ω$ is a constant. The work done by the force from $x = 0$ to $x = 2$ will be

A

$\frac{F_{0}}{ω (1 - cos ω)}$

B

$\frac{F_{0}}{2 ω (1 - cos 2 ω)}$

C

$\frac{2 F_{0} {sin}^{2} ω}{ω}$

D

$\frac{F_{0}}{ω (1 + cos 2 ω)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$W = \int_{x 1}^{x 2} F d x = \int_{0}^{2} F_{0} sin ω x d x$
$= F_{0} \frac{{| - cos ω x |}_{0}^{2}}{ω} = \frac{F_{0}}{ω} [(- cos 2 ω) - (- cos 0)]$
$= \frac{F_{0}}{ω} (1 - cos 2 ω) = \frac{F_{0}}{ω} [1 - (1 - 2 {sin}^{2} ω)]$
$= \frac{2 F_{0} {sin}^{2} ω}{ω}$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
A $- A k x$
B $A cos k x$
C $A exp (- k x)$
D $A k x$
Question 2 - Select One
A particle moving along the x axis is acted upon by a single force F = $F_{0} e^{- k x}$ , where $F_{0}$ and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :
A $F_{0} / k$
B $F_{0} / e^{k}$
C $k F_{0}$
D $k e^{k} F_{0}$
Question 3 - Select One
A force F acting on an object varies with distance x

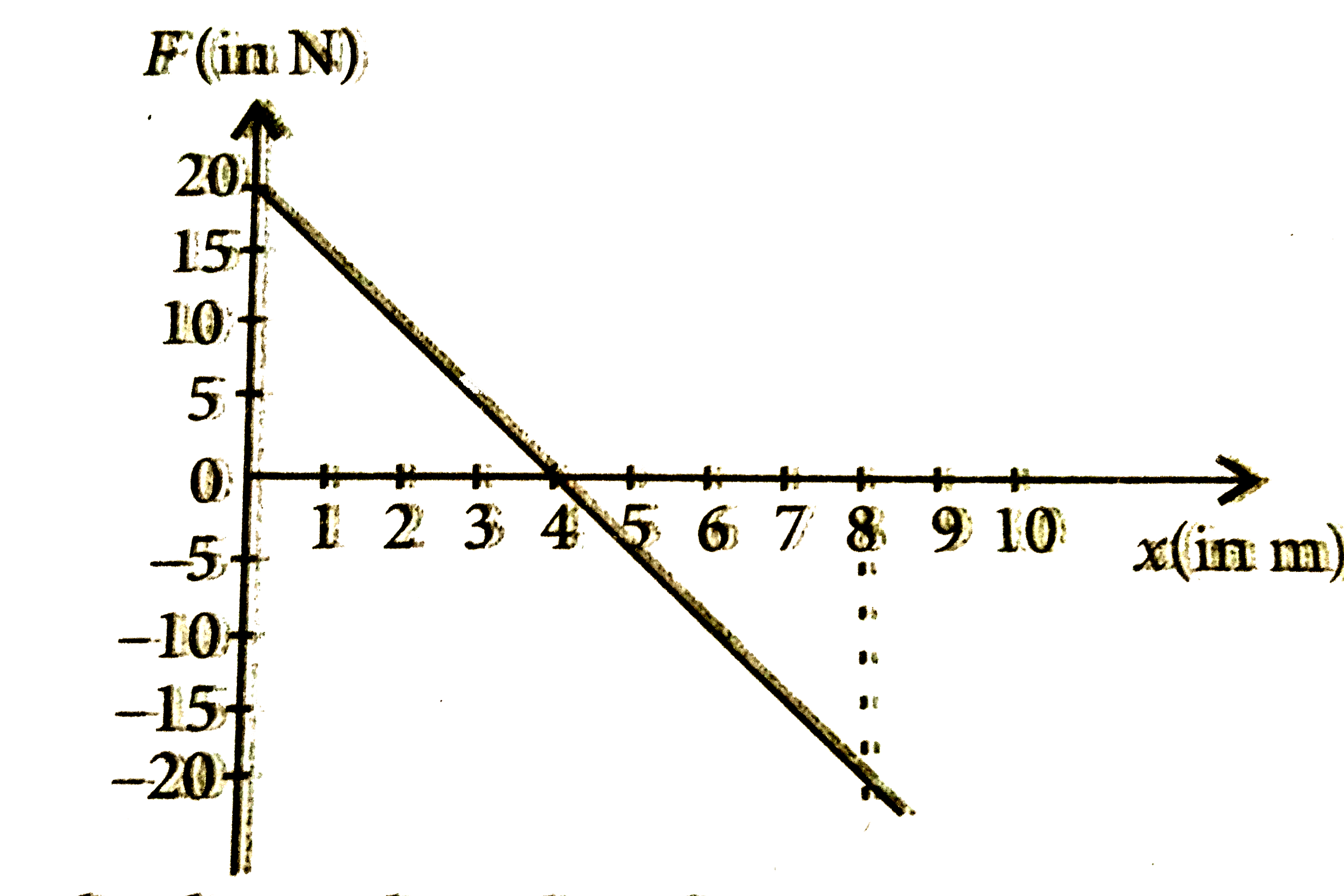
The work done by the force in moving the object from x=0 to x=8 m is
Azero
B80 J
C $- 40 J$
D $40 J$

CP SINGH-WORK, ENERGY AND POWER-EXERCISES

Home
Ask Doubt
Profile