A ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
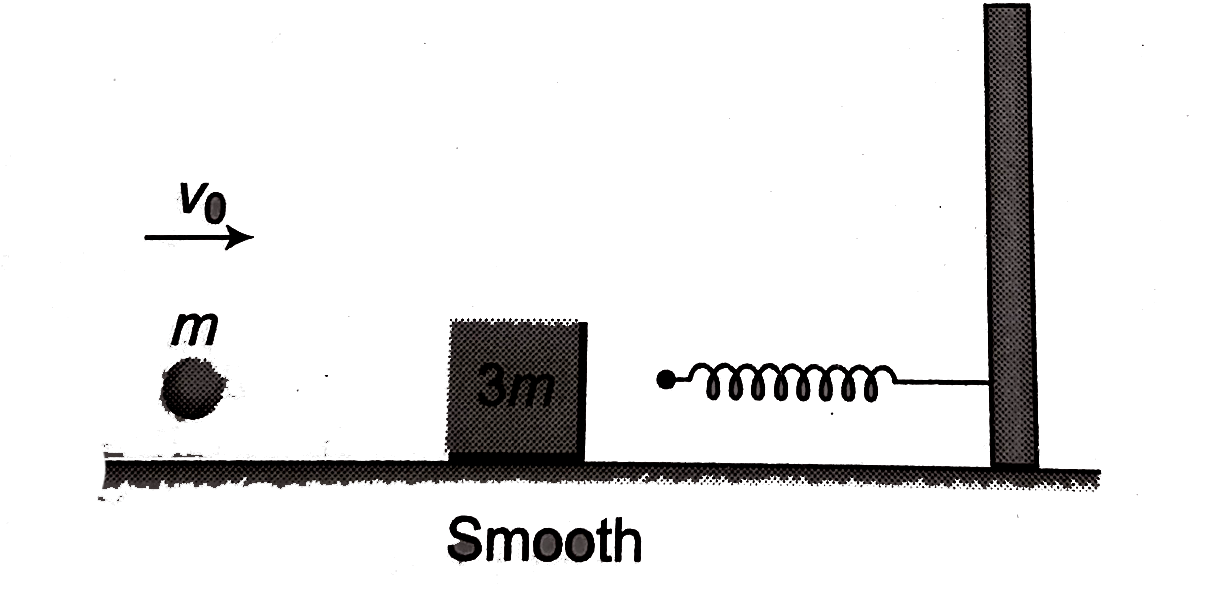
√mv20k
√mv202k
√mv203k
√mv204k
The correct Answer is:B
By the momentum conservation
mv0=(m+3m)v⇒v=v04
12(m+3m)v2=12kx20
4m(v04)2=mv204=kx20
x0=√mv204k

Topper's Solved these Questions
Similar Questions
A bullet of mass m moving with velocity u on smooth surface strikes a block of mass M kept at rest. The collision is completely inelastic. Find the common velocity and the fractional loss in kinetic energy.
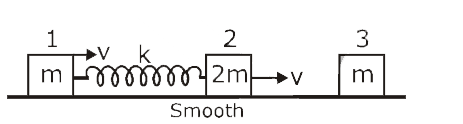
View SolutionTwo blocks 1 and 2 of masses m and 2m respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass, leading the lighter one. The spring is of natural length in the motion. Block 2 collides head on with a third block 3 of mass m, at rest, the collision being completely inelastic. Determine the velocity of blocks at the instant of maximum compression of the spring.
View Solution
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2Two block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
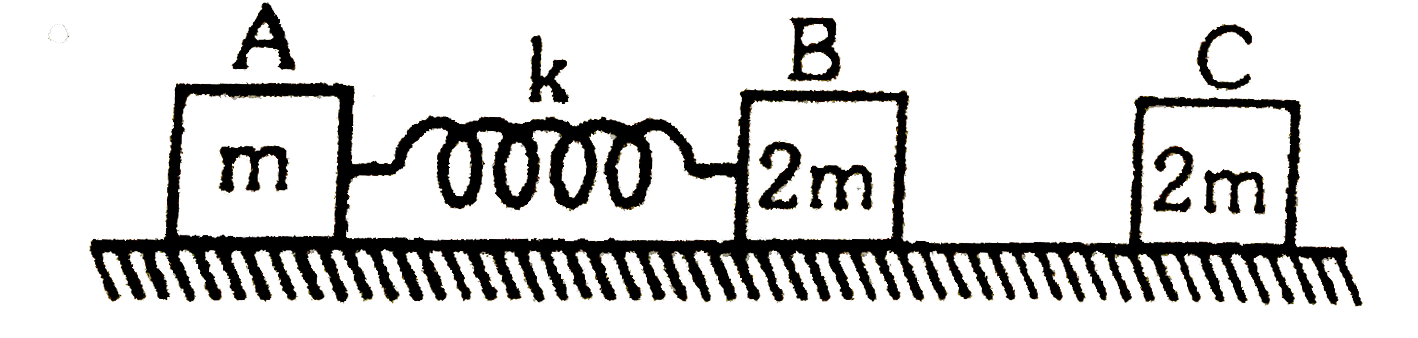
The maximum compression of the spring after collision is -A√mv2012kB√mv205kC√mv2010kDNone of theseA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 A0.5 mB0.15 mC1.5 mD0.12 m
A0.5 mB0.15 mC1.5 mD0.12 m
Two blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
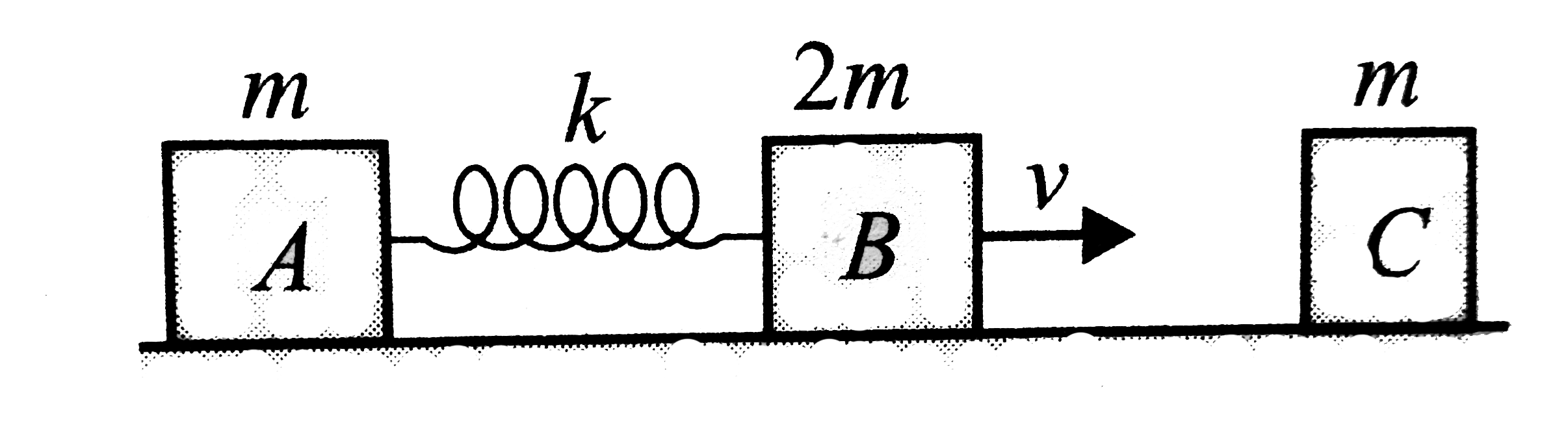
View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution

