In the previous problem , mass of the ball is and it is moving with . The surface from the block to free end of spring is rough with friction coefficient and of length . The maximum compression of spring is

The correct Answer is:B
As in the previous problem , the combined velocity
Velocity of combined mass after traveling
Let the maximum compression of spring be ,

Topper's Solved these Questions
Similar Questions
Knowledge Check
 .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.A1.48mB3.45mC4.75mD2.45mmass of 0.5 kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be
 A0.15mB0.12mC1.5mD0.5m.
A0.15mB0.12mC1.5mD0.5m.A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
A0.15 mB0.12 mC1.5 mD0.5 m
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
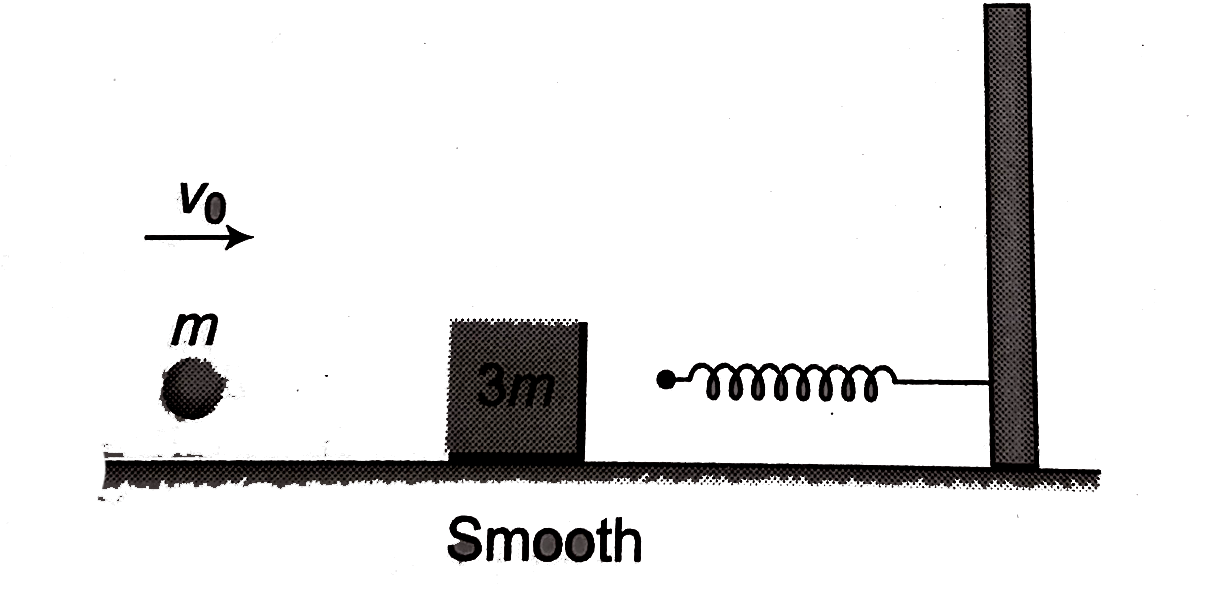
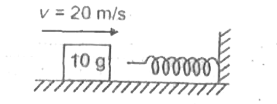
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View Solution

