Initially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)

0.1m/s
0.2m/s
0.3m/s
0.4m/s
The correct Answer is:A
When block A is released , spring regains its natural length , speed of A is v0,l is the natural length of the spring.
By the energy conservation
12k(4100)2=12×1×v20
⇒100(4100)2=v20⇒v0=0.4m/s
vc.m.=1×v0+3×01+3=0.44=0.1m/s

Topper's Solved these Questions
Similar Questions
Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
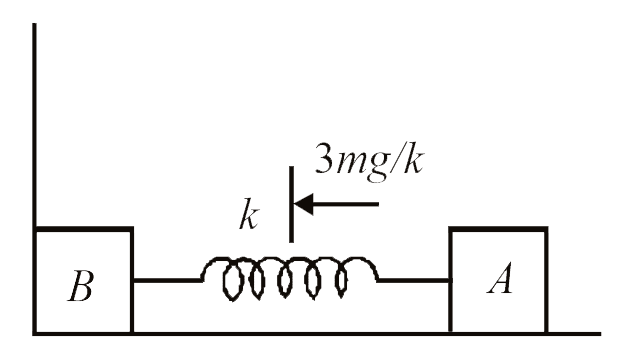
Velocity of centre of mass of system comprising A and B when block B just loses contact with the wall
View Solution
Knowledge Check
Initialy spring in its natural length now a block at mass 0.25 kg is released then find out maximum force by system on floor ?
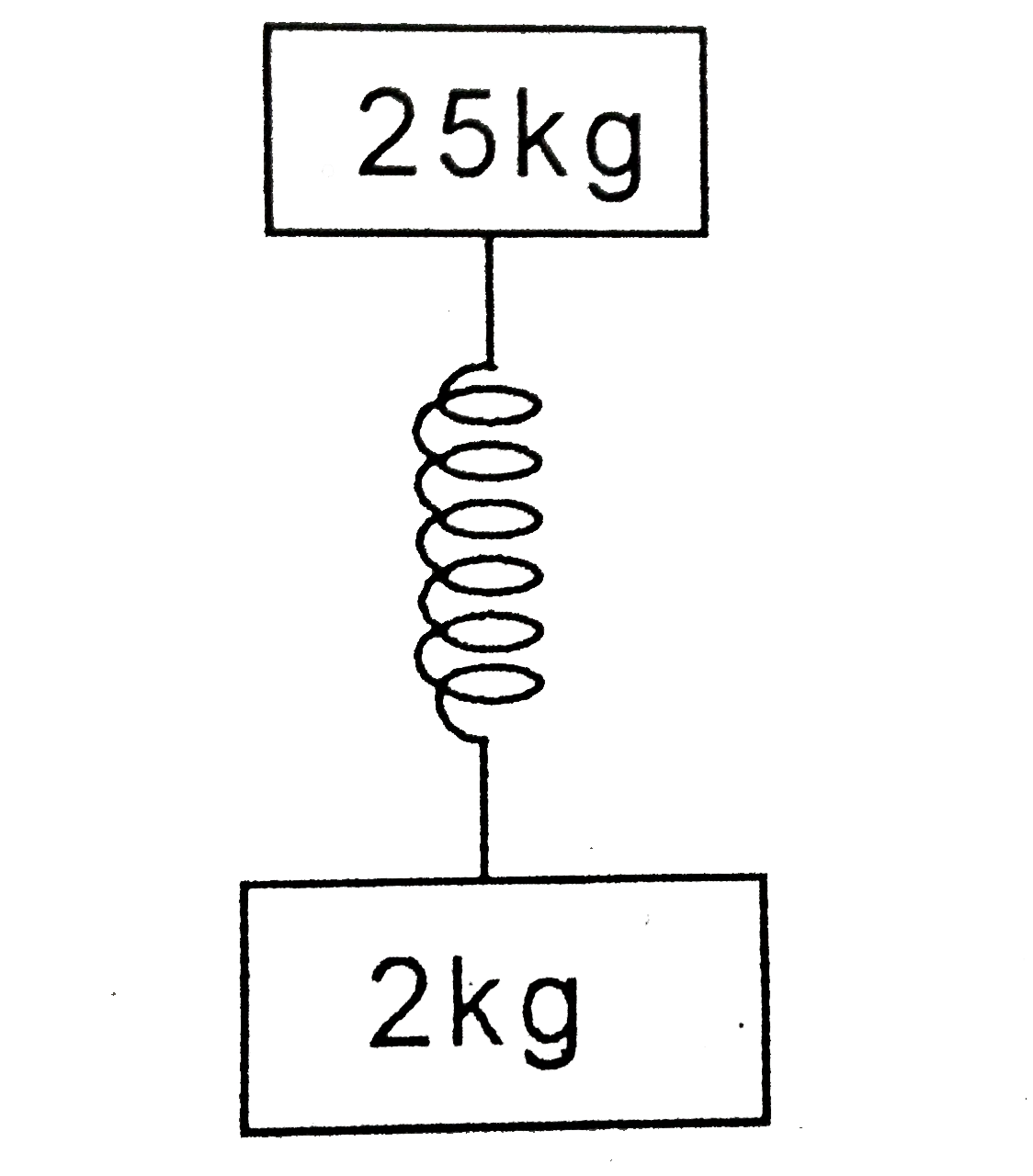 A15 NB20 NC25 ND30 N
A15 NB20 NC25 ND30 NA block of mass 1 kg is pushed towards another block of mass 2 kg from a 6 m distance as shown in the figure. If just after the collision, the velocity of 2 kg block is 4ms−1, then
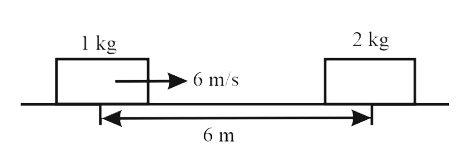 ACoefficient of restitution between the blocks is 1BCoefficient of restitution between two blocks is 1/2CCoefficient of restitution between two blocks is 1/3DCoefficient of restitution between two blocks is 1/4
ACoefficient of restitution between the blocks is 1BCoefficient of restitution between two blocks is 1/2CCoefficient of restitution between two blocks is 1/3DCoefficient of restitution between two blocks is 1/4A block (A) of mass 3 kg in contact with a second block (B) of mass 2 kg rests on a frictionless horizontal surface. A horizontal force of 20 N is applied to push the block A. What is the force with which the block A pushes the block B?
A4NB6NC8ND10N
Initially spring is in natural length and block of mass m is released from rest what should be the minimum value of M (in kg) to just move the 2kg block. If this minimum value is x8kg. Find x

View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
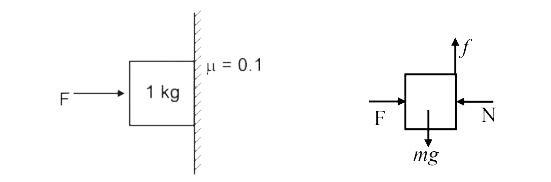
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View SolutionA force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
View SolutionA block A of mass M is placed in contact with a fixed spring of length l and force constant k and free from a smooth wall at a distance l on the other side. If the block is given a velocity v as shown, the time taken by the block to strike on the wall will be

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View Solution

