Initially spring is in natural length and block of mass m is released from rest what should be the minimum value of M (in kg) to just move the 2kg block. If this minimum value is x8kg. Find x

The correct Answer is:6
With respect to free end, velocity of block is 3 m/s leftward. In position of maximum extension, the block will stop w.r.t. free end. As observed from free end, which is inertial frame 12kx2=12mv2
x=√mv2k=3√mk=3√1104=3×10−2 meter = 3 cm
Topper's Solved these Questions
Similar Questions
In the given figure if system is released from rest,then find the minimum value of coefficient of friction such that block A of mass 2m does not move.
View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
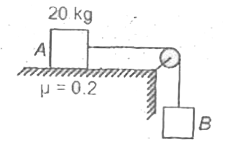
View Solution
Knowledge Check
Initialy spring in its natural length now a block at mass 0.25 kg is released then find out maximum force by system on floor ?
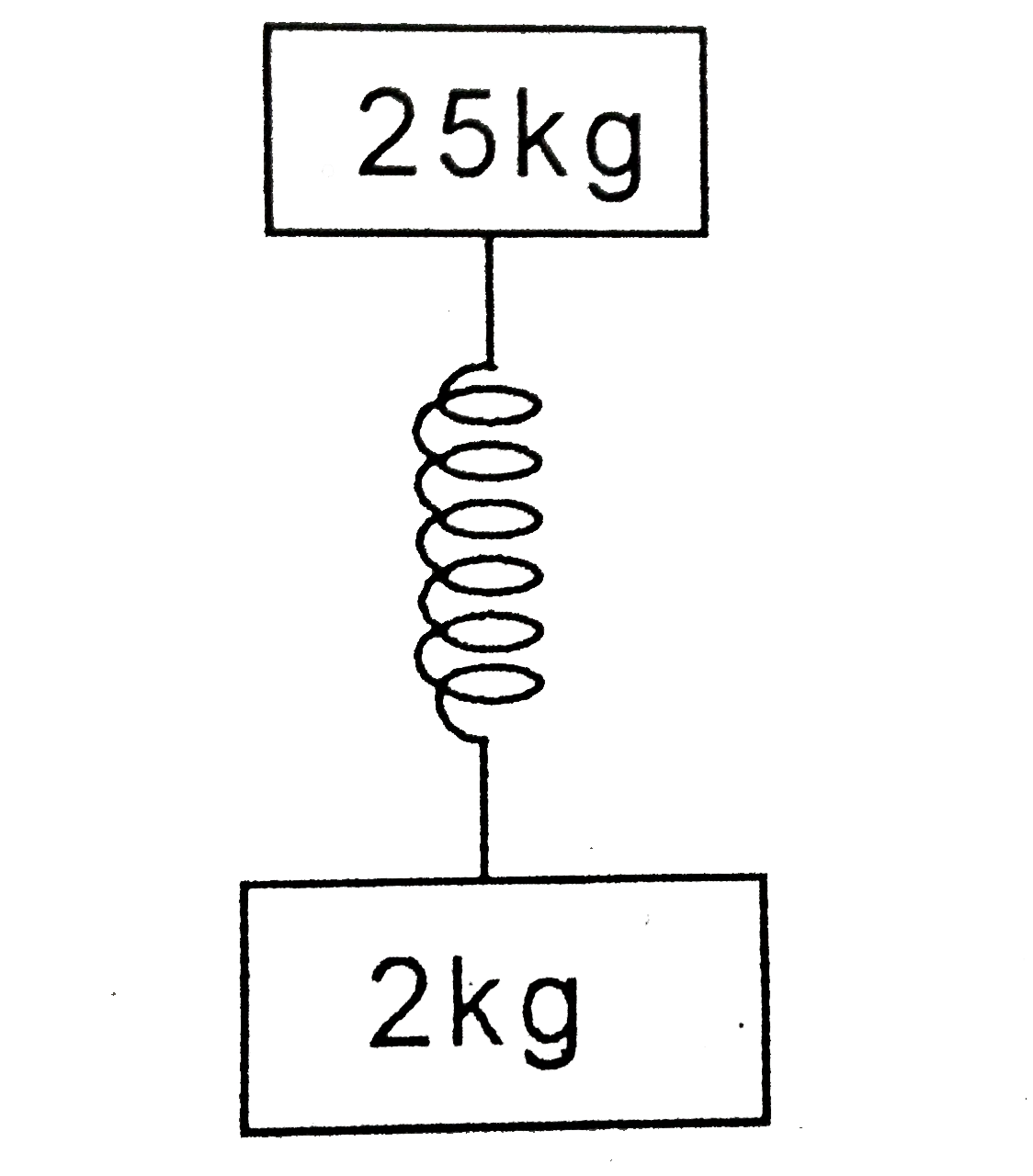 A15 NB20 NC25 ND30 N
A15 NB20 NC25 ND30 NA block of mass m is attached with a massless spring of force constant k. The block is placed over a fixed rought inclined surface for which the coefficient of friction is μ=34 . The block of mass m is initially at rest . The block is mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is ( neglect mass of string and pulley and friction in pulley )
 A35mB45mC65mD32m
A35mB45mC65mD32mWhat should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10m/s2)
 A12 kgB8 kgC10 kgD6 kg
A12 kgB8 kgC10 kgD6 kg
What should be minimum value of F so that 2 kg slides on ground but 1kg does not slide on it? [g=10msec2]
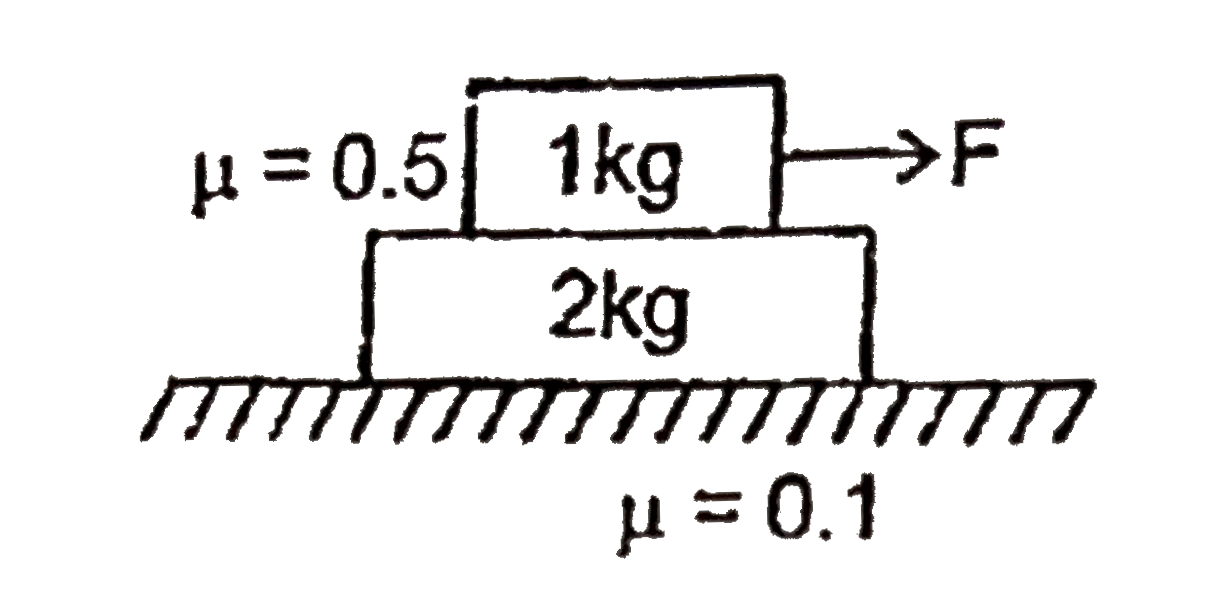
View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.

View SolutionInitially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)

View SolutionIn the figure, the ball B is released from rest when the spring is in natural length. For the block A of mass 2m to leave contact with the ground at some instant the minimum mass of B must be

View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View Solution

