In the figure, the ball B is released from rest when the spring is in natural length. For the block A of mass 2m to leave contact with the ground at some instant the minimum mass of B must be

2m
m
m2
m4
The correct Answer is:D
Using conservation of momentum,
2mV=√m2v2+m2v2
2mV=√2m2v2
V=v√2]
Energy released in explosion =2×12mv2+12×2m×v22=32mv2
Topper's Solved these Questions
Similar Questions
In the arrangement shown in the fig. string, springs and the pulley are mass less. Both the springs have a force constant of k and the mass of block B resting on the table is M. Ball A is released from rest when both the springs are in natural length and just taut. Find the minimum value of mass of A so that block B leaves contact with the table at some stage
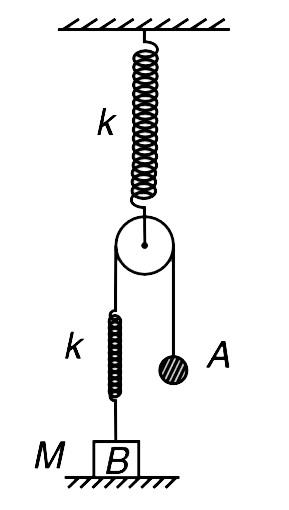
View SolutionIn the arrangement shown in the figure, block B of mass M rests on a weighing scale. Ball A is released from a position where spring is in its natural length and the scale shows the correct weight of block B. Find the mass of ball A so that the minimum reading shown by the scale subsequently is half the true weight of B.
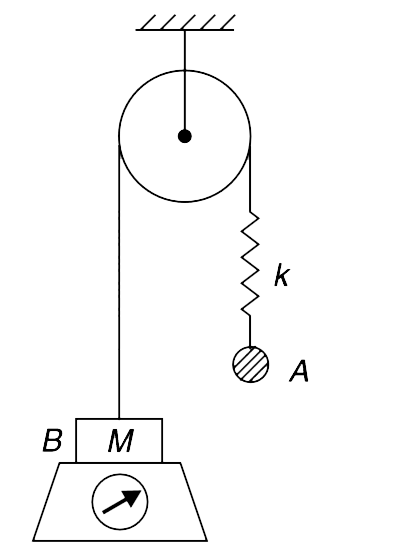
View Solution
Knowledge Check
In figure, block A is released from rest, when spring is at its natural unstretched length. For block B of mass M to leave contact with the ground at some stage, the minimum mass of A must be
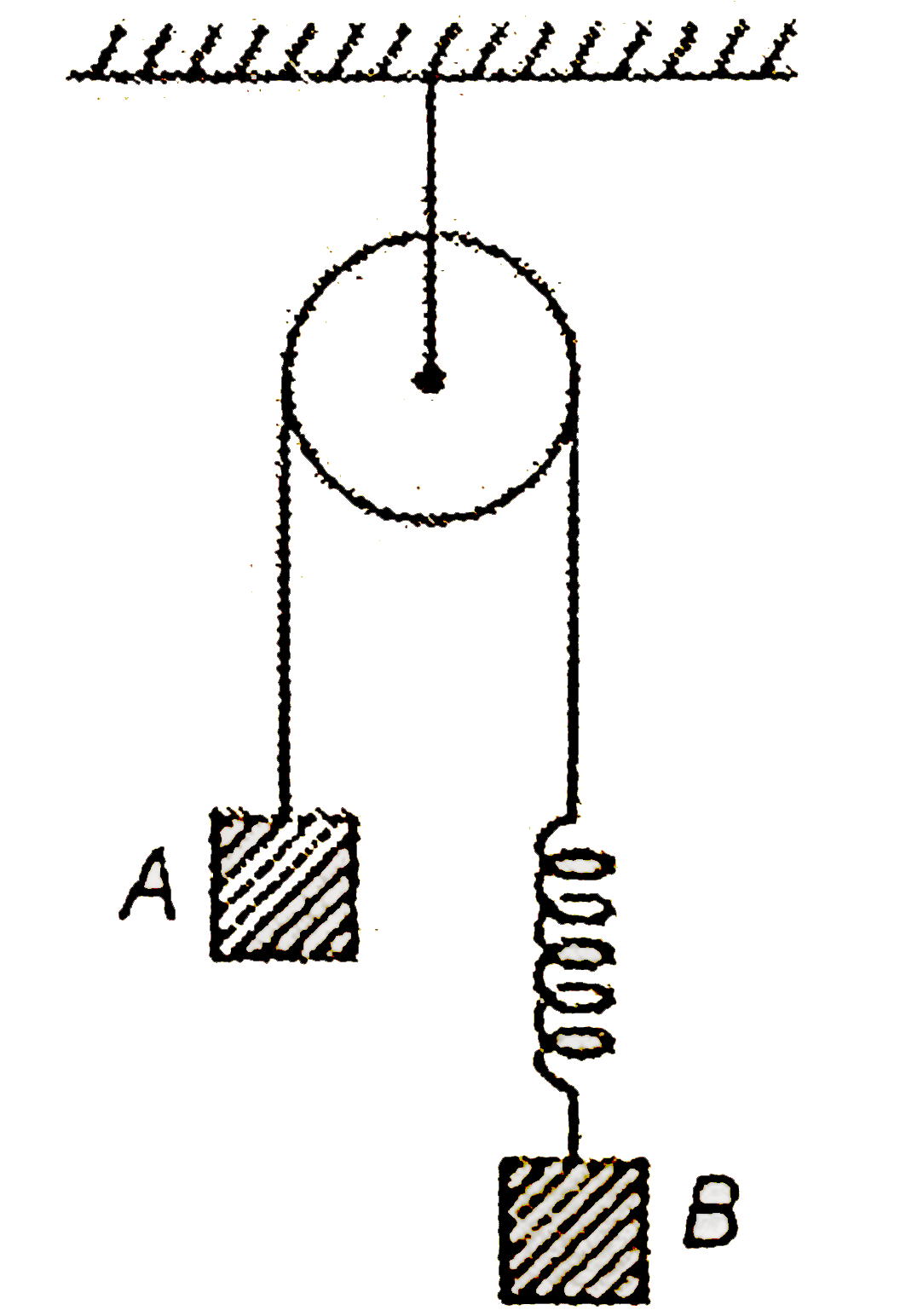 A3MBM2CMDcannot say
A3MBM2CMDcannot sayIn the adjoining diagram the ball A is released from rest when the spring is at its natural length (neither stretched nor compressed) For the block B of mass M to leave contact with the ground at some time, the minimum mass of A must be:
 AM2BMC2MDa function of M and force constant k of spring
AM2BMC2MDa function of M and force constant k of springThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
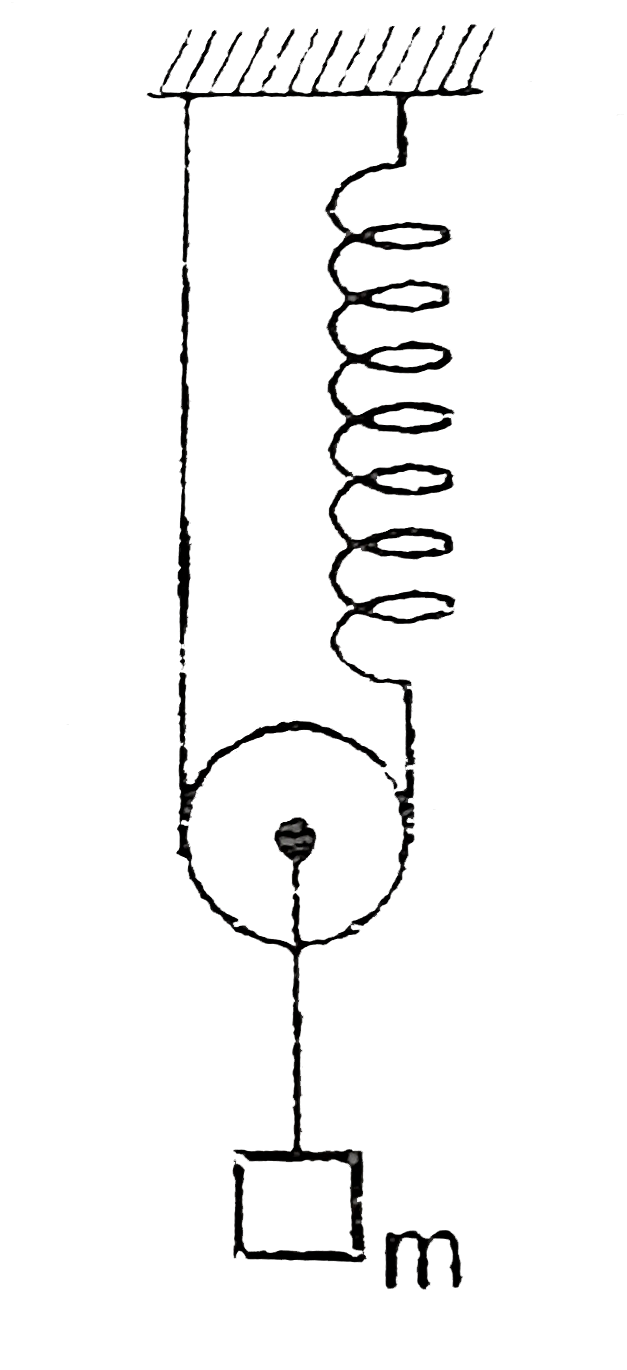 A1 mB12mC2 mD2.5 m
A1 mB12mC2 mD2.5 m
In the given figure if system is released from rest,then find the minimum value of coefficient of friction such that block A of mass 2m does not move.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)

View SolutionBlock m is released from rest when spring is in its natural length ( assume pulley is ideal and block does not strike on ground during it's motion in vertical plane )
than :
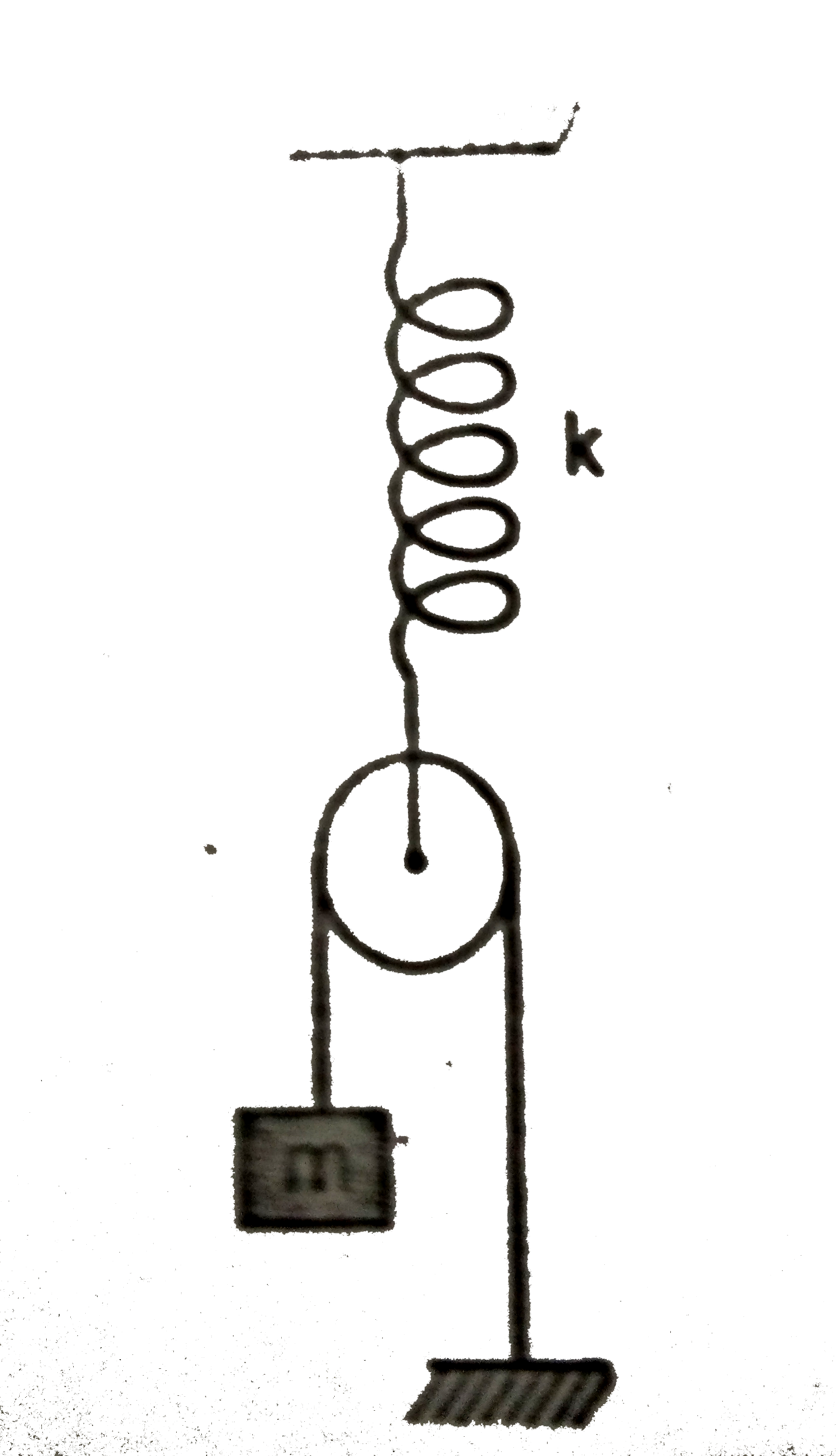
View SolutionIn the given figure balls A&B are released simultaneously , when string is horizontal , length of strings are same but mass of ball B is twice of mass of ball A. Then
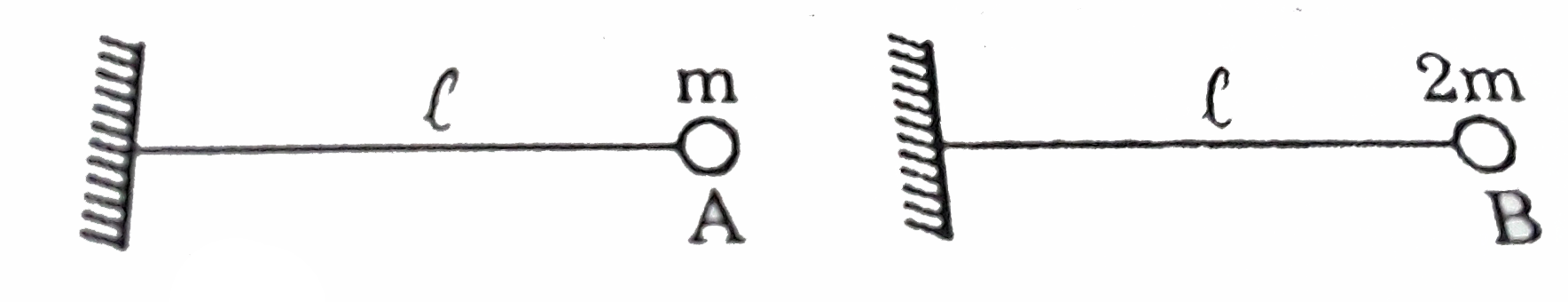
View Solution
