Block m is released from rest when spring is in its natural length ( assume pulley is ideal and block does not strike on ground during it's motion in vertical plane )
than :
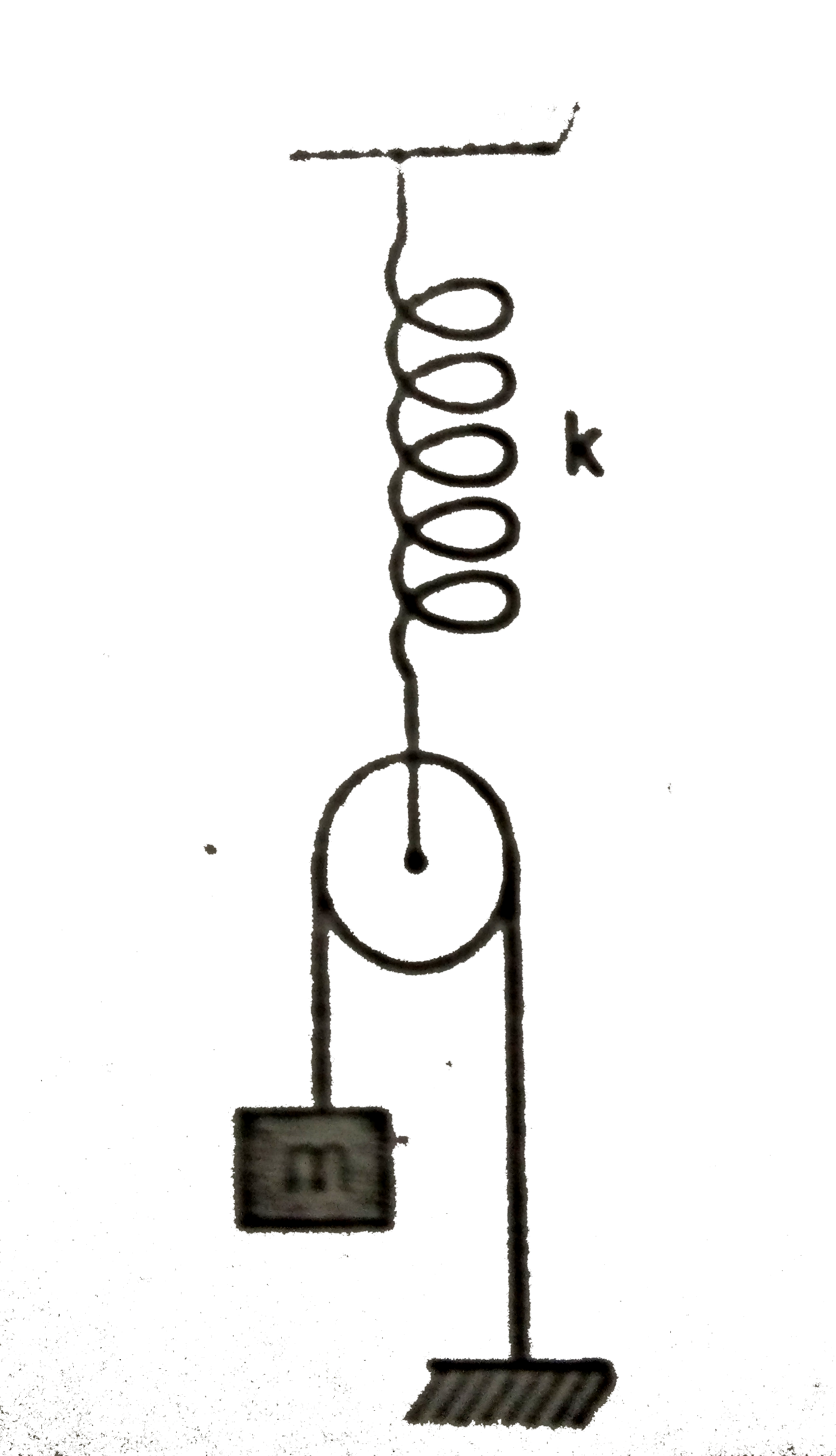
maximum elongation in spring is 4mg/k
maximum elongation in spring is 2mg/k
maximum speed of block is 2g√mk
maximum speed of block is g√mk
The correct Answer is:A, C
By energy conservation 12kx2=mg(2x)
⇒x=4mgk( maximum elongation )
at equilibrium kx=2mg
⇒x=2mgk
So (K.E.)max=mg(2x)−12kx2
=2mg(2mgk)−12k(2mgk)2
12mv2max=2m2g2k
⇒vmax=2g√mk
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 41
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 42
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 39
Explore 3 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
Initially spring is at it's natural length and collision is elastic. Then find maximum compression of spring during motion :
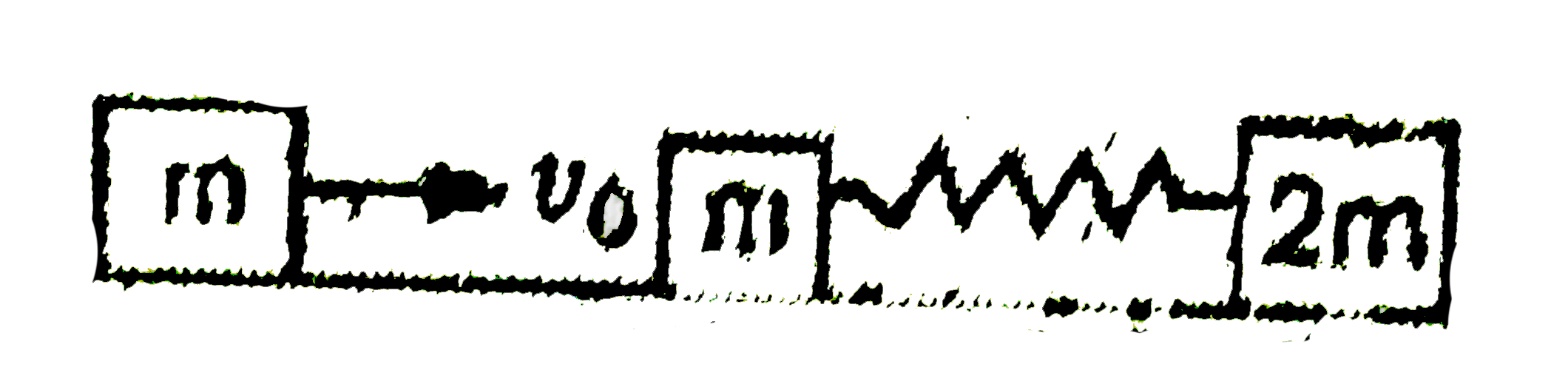 A√2m3kυ0B√3m2kυ0C√m2kυ0D√mkυ0
A√2m3kυ0B√3m2kυ0C√m2kυ0D√mkυ0The given arrangement is released from rest when spring is in natural length. Maximum extension in spring during the motion is x0.a1,a2 and a3 are accelerations of the blocks. Make the correct options
_PHY_E01_005_Q01.png) Aa2−a1=a1−a3Bx0=4mg3kCVelocity of 2m connected to spring when elongation is x02 is v=x02√3k14mDacceleration a1 at x04 is 3kx042m
Aa2−a1=a1−a3Bx0=4mg3kCVelocity of 2m connected to spring when elongation is x02 is v=x02√3k14mDacceleration a1 at x04 is 3kx042mIn figure, block A is released from rest, when spring is at its natural unstretched length. For block B of mass M to leave contact with the ground at some stage, the minimum mass of A must be
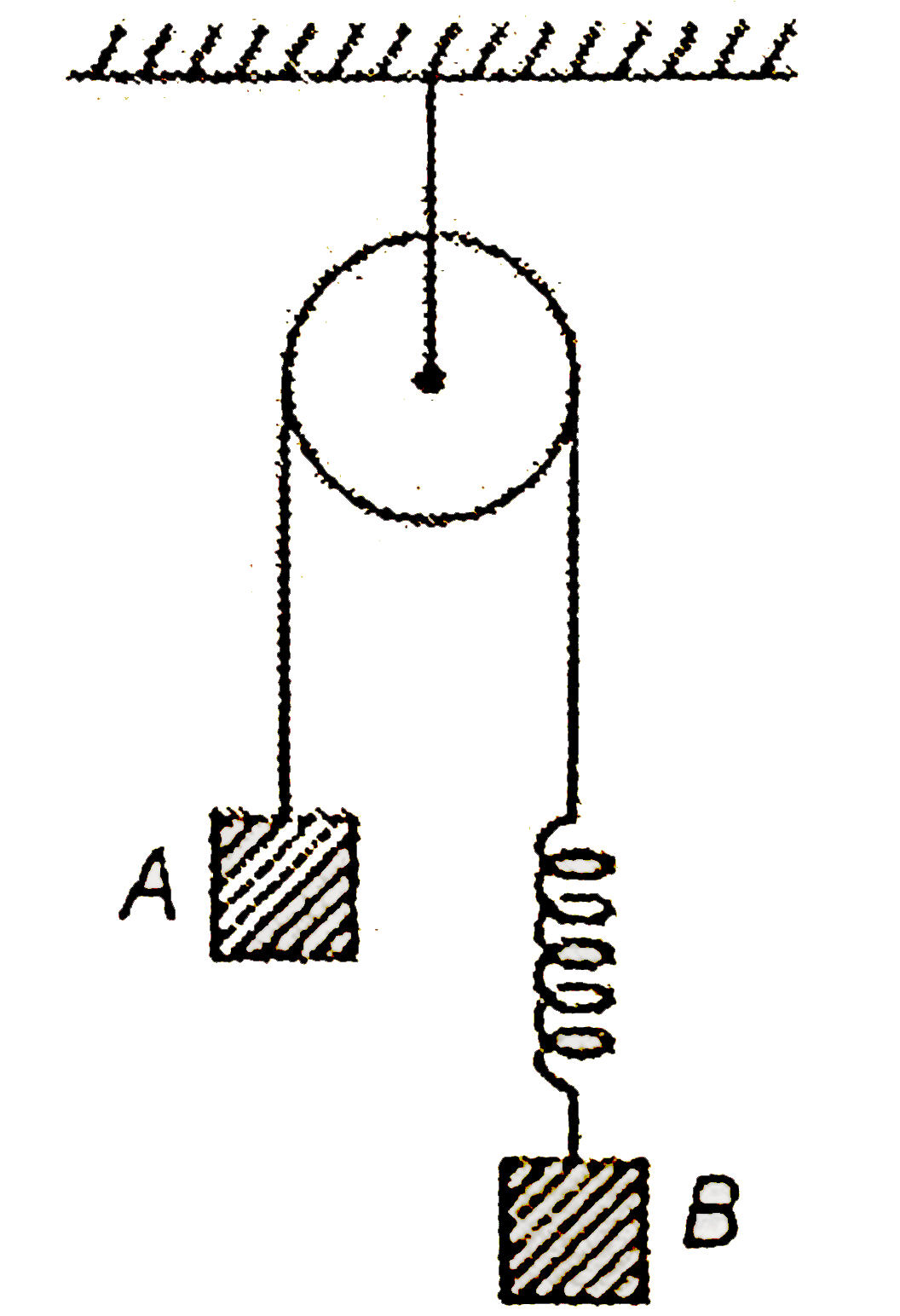 A3MBM2CMDcannot say
A3MBM2CMDcannot say
In the adjoining diagram the ball A is released from rest when the spring is at its natural length (neither stretched nor compressed) For the block B of mass M to leave contact with the ground at some time, the minimum mass of A must be:

View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
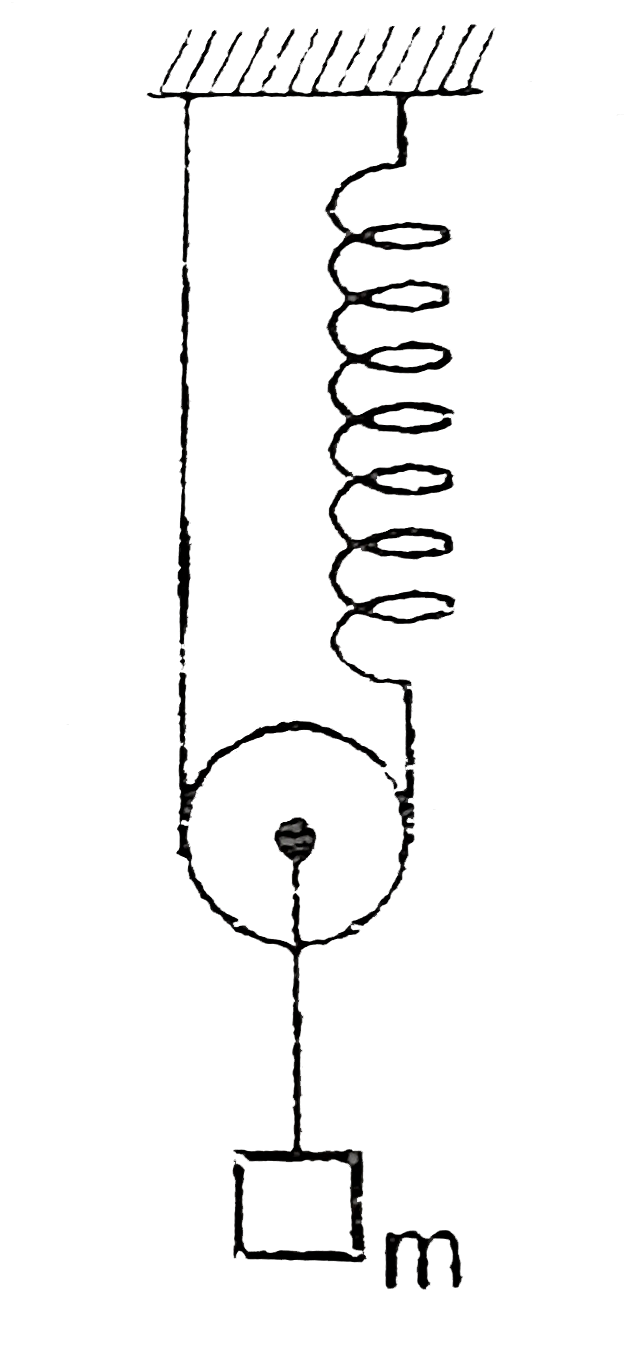
View SolutionIn the figure, the ball B is released from rest when the spring is in natural length. For the block A of mass 2m to leave contact with the ground at some instant the minimum mass of B must be

View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View Solution