Two objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time t=0. The distance moved by the object when one overtakes the
6u2a
2u2a
4u2a
None of these
The correct Answer is:A
Let both will meet at point B
x=2ut+12at2
x=ut+12(2a)t2
So 2ut+12at2=ut+at2
ut=12at2⇒t=2ua
So x=2u(2ua)+12a(2ua)2=6u2a
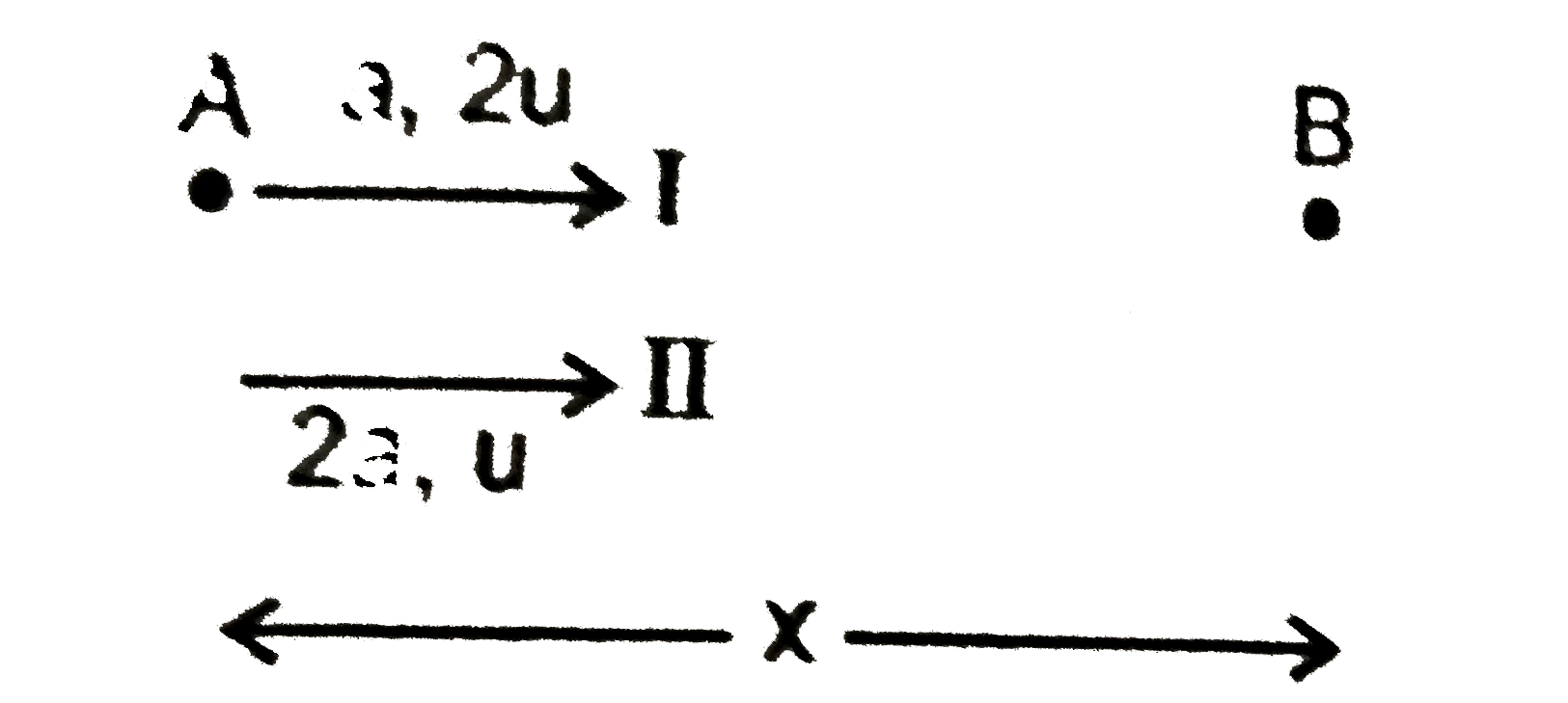
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 40
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 41
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 38
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Knowledge Check
Two objects moving along the same straight line are leaving point A with an acceleration a, 2a and velocity 2u,u respectively at time t=0. The distance moved by the object with respect to point A when one object overtakes the other is :
A3u2aB2u2aC4u2aD6u2aAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
Au+12atBu+atCu+at2Du2At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity vafter time t, is
Av=u+atBv=u+at2Cv=u+12at2Dv=at2

For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View SolutionShow that the area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in that interval.
View SolutionShow that area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in the interval.
View SolutionAt the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity v after time t, is
View SolutionTwo objects move in the same direction in a straight line. One moves with a constant velocity V1.The other starts at rest and has constant acceleration a. They collide when the second object has velocity 2V1.The distance between the two objects when the second one starts moving is :
View Solution