Show that area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in the interval.
To show that the area under the velocity-time graph of an object moving with constant acceleration in a straight line during a certain time interval is equal to the distance covered by the object in that interval, we can follow these steps:
Step 1: Understand the motion of the object
The object is moving in a straight line with constant acceleration. We denote:
- Initial velocity = u
- Acceleration = a
- Time interval = t1
Step 2: Write the equation for velocity
The velocity of the object at any time t can be expressed as:
v=u+at
where v is the final velocity at time t.
Step 3: Draw the velocity-time graph
For a constant acceleration, the velocity-time graph will be a straight line. At t=0, the velocity is u, and at t=t1, the velocity becomes:
v=u+at1
This gives us two points on the graph:
- Point A (0, u)
- Point B (t1, u+at1)
Step 4: Identify the shape of the area under the graph
The area under the velocity-time graph from t=0 to t=t1 forms a trapezium (or trapezoid) with the following bases:
- Base 1 = u (initial velocity)
- Base 2 = u+at1 (final velocity)
- Height = t1 (time interval)
Step 5: Calculate the area of the trapezium
The area A of a trapezium is given by the formula:
A=12×(Base1+Base2)×Height
Substituting the values we have:
A=12×(u+(u+at1))×t1
A=12×(2u+at1)×t1
A=(u⋅t1)+12at21
Step 6: Relate the area to the distance covered
The distance s covered by the object during the time interval t1 can be calculated using the equation of motion:
s=ut1+12at21
Step 7: Compare the area and distance
From our calculations:
- Area under the velocity-time graph = ut1+12at21
- Distance covered = ut1+12at21
Since both expressions are equal, we conclude that:
Area under the velocity-time graph=Distance covered by the object
Conclusion
Thus, we have shown that the area under the velocity-time graph of an object moving with constant acceleration in a straight line during a certain time interval is equal to the distance covered by the object in that interval.
---
The object is moving in a straight line with constant acceleration. We denote:
- Initial velocity = u
- Acceleration = a
- Time interval = t1
The velocity of the object at any time t can be expressed as:
v=u+at
where v is the final velocity at time t.
For a constant acceleration, the velocity-time graph will be a straight line. At t=0, the velocity is u, and at t=t1, the velocity becomes:
v=u+at1
This gives us two points on the graph:
- Point A (0, u)
- Point B (t1, u+at1)
The area under the velocity-time graph from t=0 to t=t1 forms a trapezium (or trapezoid) with the following bases:
- Base 1 = u (initial velocity)
- Base 2 = u+at1 (final velocity)
- Height = t1 (time interval)
The area A of a trapezium is given by the formula:
A=12×(Base1+Base2)×Height
Substituting the values we have:
A=12×(u+(u+at1))×t1
A=12×(2u+at1)×t1
A=(u⋅t1)+12at21
The distance s covered by the object during the time interval t1 can be calculated using the equation of motion:
s=ut1+12at21
From our calculations:
- Area under the velocity-time graph = ut1+12at21
- Distance covered = ut1+12at21
Area under the velocity-time graph=Distance covered by the object
Thus, we have shown that the area under the velocity-time graph of an object moving with constant acceleration in a straight line during a certain time interval is equal to the distance covered by the object in that interval.
Topper's Solved these Questions
Similar Questions
Show that the area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in that interval.
View SolutionDraw the velocity-time graph of an object moving with uniform negative acceleration.
View SolutionDraw the velocity-time graph of an object moving with uniform positive acceleration.
View SolutionDraw the position-time graph of a moving object, moving with zero acceleration.
View SolutionThe distance-time graph of the motion of an object moving with a contant speed is a straight line.
View SolutionThe distance-time graph of the motion of an object moving with a contant speed is a straight line.
View SolutionThe velocity-time graph of an object is shown below. The acceleration of the object is
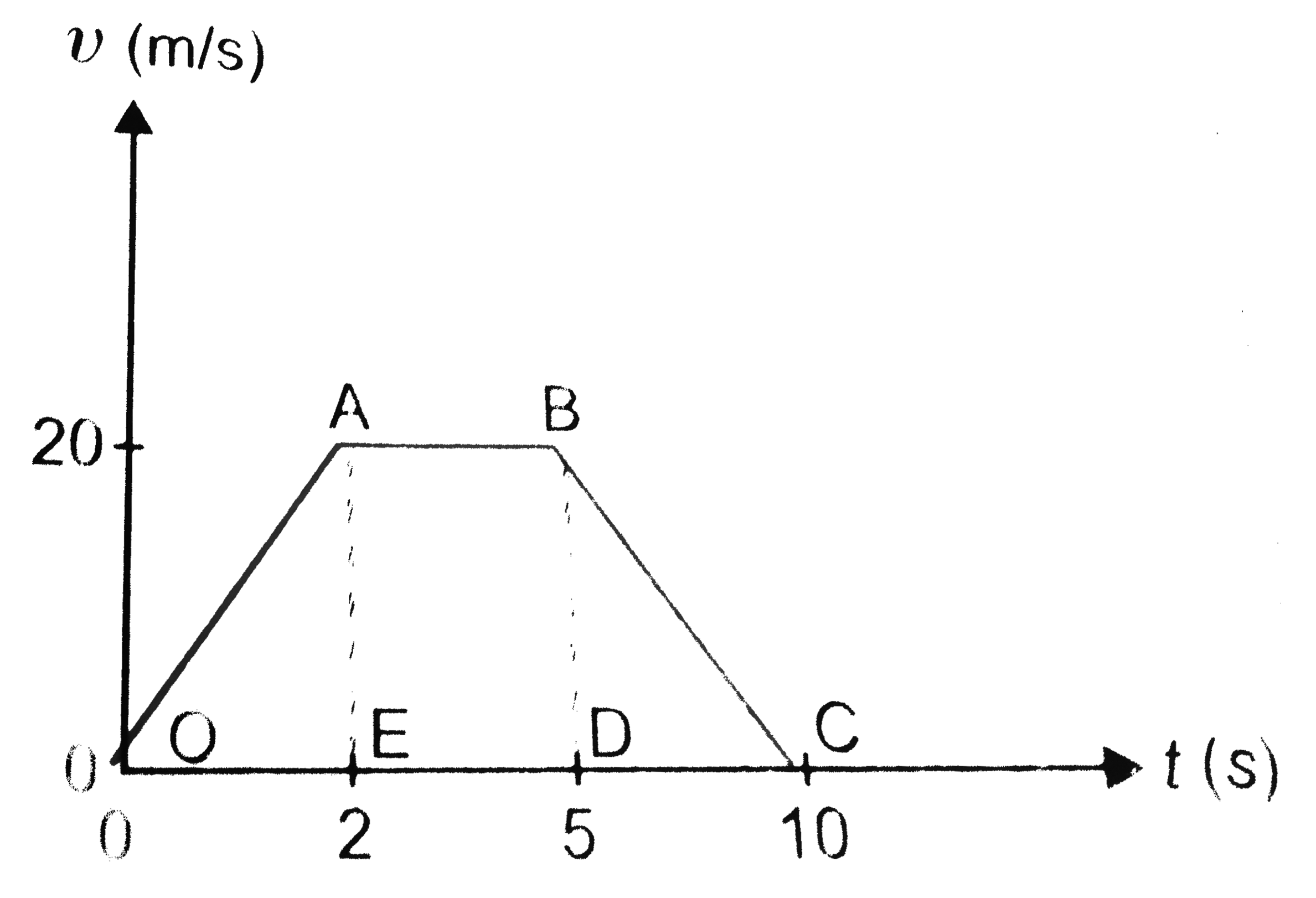
View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between (i)t=0→t=5s (ii) t=0→t=10s.
 .
.
View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between (i)t=0→t=5s (ii) t=0→t=10s.
 .
.
View SolutionThe velocity-time graph of an object is given below. Calculate the average acceleration of the object in the time interval of 4 s to 6 s.

View Solution