A particle is projected at an angle of 30∘w.r.t. horizontal with speed 20m/s:( use g=10m/s2)
(i) Find the position vector of the particle after 1s.
(ii) Find the angle between velocity vector and position vector at t=1s.
The correct Answer is:(i) 1−0√3ˆi+5ˆj
(ii) cos−1(2√313)
(i)x=ucosθt
=20×√32×t=10√3m
y=usinθt−12×10×t2
=20×12×(1)−5(1)2=5m
Position vector, →r=10√3ˆi+5ˆj
|→r|=√(10√3)2+52
(ii)vx=10√3ˆi
vy=uy+ayt=10−gt=0
∴→v=10√3ˆi,|→v|=10√3
→v.→r=(10√3ˆi).(10√3ˆi+5ˆj)=300
→v.→r=|→v||→r|cosθ
⇒cosθ=→v.→r|→v||→r|=30010√3√325
⇒θ=cos−1(2√313)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 41
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 42
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 39
Explore 3 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionA particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View Solution
Knowledge Check
A particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)
 A5mB15mC10mD0
A5mB15mC10mD0The position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle isAparallel to position vecorBperpendicular to position vectorCdirected towards originDdirected awa from the originA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
A0∘B30∘C60∘D90∘
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
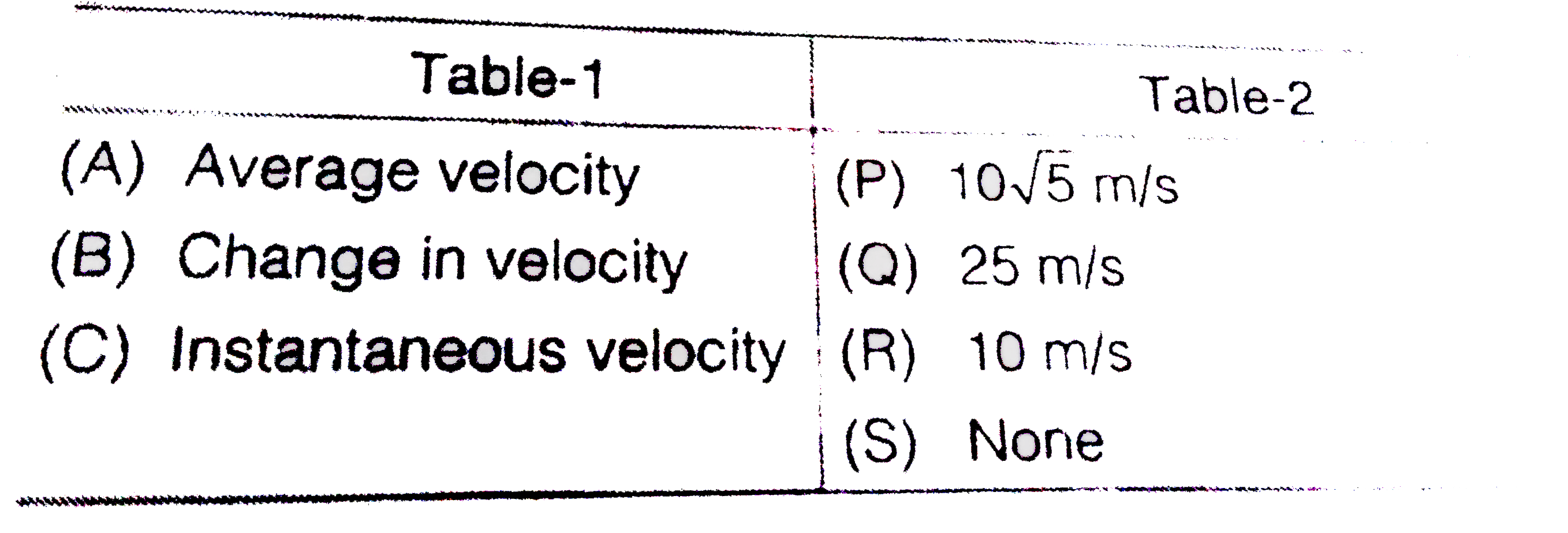
View SolutionA particle is projected with speed 100ms at angle θ=60∘ with the horizontal at time t=0" . At time 't' the velocity vector of the particle becomes perpendicular to the direction of velocity of projection.Its tangential acceleration at time 't' is (g=10ms2)
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionThe position vector of a particle is →r=acosωti+asinωtj, the velocity of the particle is
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View Solution

