A small hoop of mass m is given an initial velocity of magnitude v0 on the horizontal circular ring of radius 'r'. If the coefficient of kinetic friction is μk the tangential acceleration of the hoop immediately after is release is ( assume the horizontal ring to be fixed and not in contact with any supporting surface )
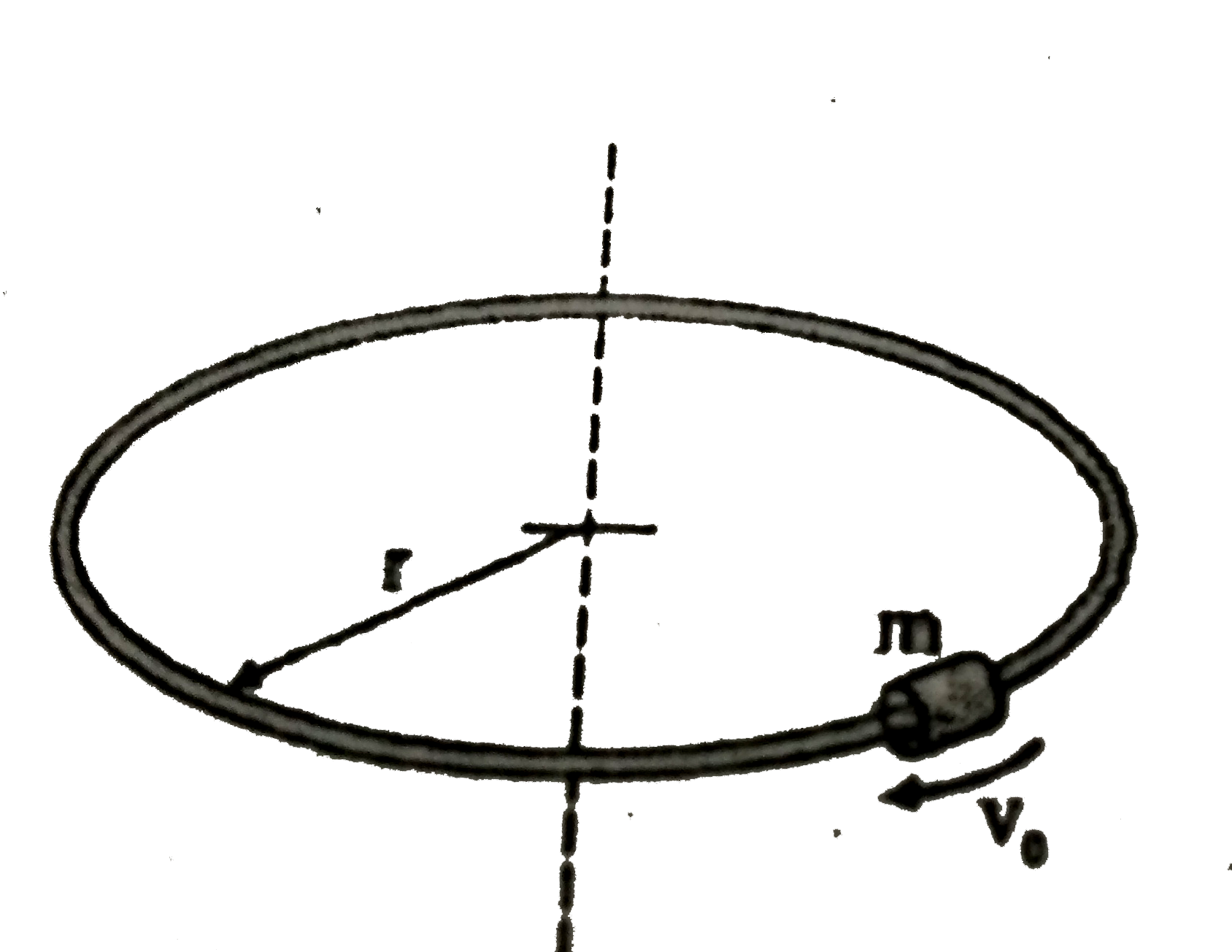
μk√g2+V40r2
μkg
μk(V20r)
None of these
The correct Answer is:C
K.E.=121cmω2+12mV2cm=12Ml212V20l2+12M(32V0)2=76MV20
Topper's Solved these Questions
Similar Questions
A small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View SolutionA small bead of mass m is given an initial velocity of magnitude v0 on a horizontal circular wire. If the coefficient of kinetic friction is μk, determine the distance travelled before the collar comes to rest.
View Solution
Knowledge Check
A small collar of mass m is given an intial velocity of magnitude v0 on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is μK, determine the distance travelled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).
 Arμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦Br4μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦C2rμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦Dr2μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦
Arμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦Br4μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦C2rμkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦Dr2μkln⎡⎢ ⎢⎣v20+√v40+r2g2rg⎤⎥ ⎥⎦A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
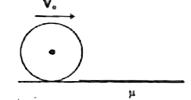 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
Aω0μkR2gBω0g2μkRC2ω0RμkgDω0R2μkg
A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0=ax. Find the kinetic energy of the block as function of x before it comes to rest.
View Solution
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
View SolutionA particle of mass m is given a velocity u on a rough horizontal surface of friction coefficient μ. The average power imparted by friction until it stops is
View SolutionA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
View SolutionA ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
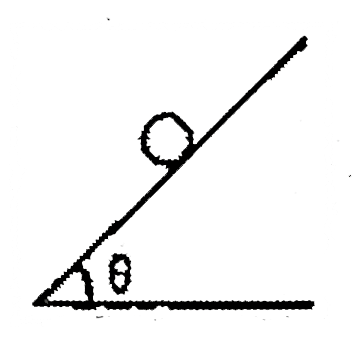
View Solution
