A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
mg(h−d)+12Kd2
mg(h+d)+12Kd2
mg(h+d)−12Kd2
mg(h−d)−12Kd2
The correct Answer is:C
To solve the problem, we need to calculate the net work done when a ball of mass m falls from a height h and compresses a vertical spring by a distance d.
1. Identify Forces Acting on the Ball:
- The gravitational force acting on the ball is Fg=mg, where g is the acceleration due to gravity.
- As the ball compresses the spring, the spring exerts an upward force given by Hooke's Law: Fs=kx, where x is the compression of the spring.
2. Calculate Work Done by Gravity:
- The ball falls a total distance of h+d (it falls h to reach the spring and then compresses the spring by d).
- The work done by gravity Wg is positive because the force and displacement are in the same direction:
Wg=Fg⋅displacement=mg(h+d)
3. Calculate Work Done by the Spring:
- The work done by the spring Ws is negative because the spring force acts in the opposite direction to the displacement of the ball:
Ws=−12kd2
- This is derived from the work done on a spring, which is 12kx2 for compression x.
4. Calculate Net Work Done:
- The net work done Wnet is the sum of the work done by gravity and the work done by the spring:
Wnet=Wg+Ws
- Substituting the expressions we found:
Wnet=mg(h+d)−12kd2
Final Answer:
The net work done in the process is:
Wnet=mg(h+d)−12kd2
- The gravitational force acting on the ball is Fg=mg, where g is the acceleration due to gravity.
- As the ball compresses the spring, the spring exerts an upward force given by Hooke's Law: Fs=kx, where x is the compression of the spring.
- The ball falls a total distance of h+d (it falls h to reach the spring and then compresses the spring by d).
- The work done by gravity Wg is positive because the force and displacement are in the same direction:
Wg=Fg⋅displacement=mg(h+d)
- The work done by the spring Ws is negative because the spring force acts in the opposite direction to the displacement of the ball:
Ws=−12kd2
- This is derived from the work done on a spring, which is 12kx2 for compression x.
- The net work done Wnet is the sum of the work done by gravity and the work done by the spring:
Wnet=Wg+Ws
- Substituting the expressions we found:
Wnet=mg(h+d)−12kd2
The net work done in the process is:
Wnet=mg(h+d)−12kd2
Similar Questions
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA vertical spring of force cosntant 100N/m is attached with a hanging mass of 10 kg. Now an external force is applied on the mass so that the spring is stretched by additional 2m. The work done by the force F is (g=10m/s2)
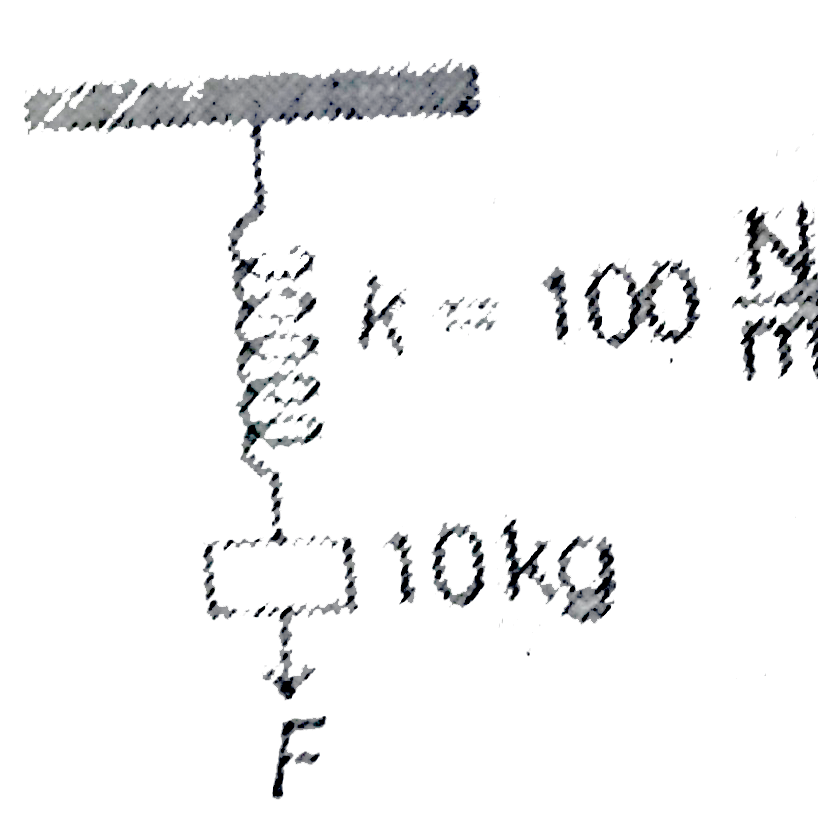
View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View SolutionTwo light spring of force constants k1andk2 and a block of mass m are in the line AB on a smooth horizontal table such that one end of each spring is fixed on right supports and the other end is free as shown in figure

The distance CD between the free ends of the spring is 60cm. If the block (k1=1.8N/m,k2=3.2N/mandm=200g). Is the motion simple harmonic?
View Solution
