Question

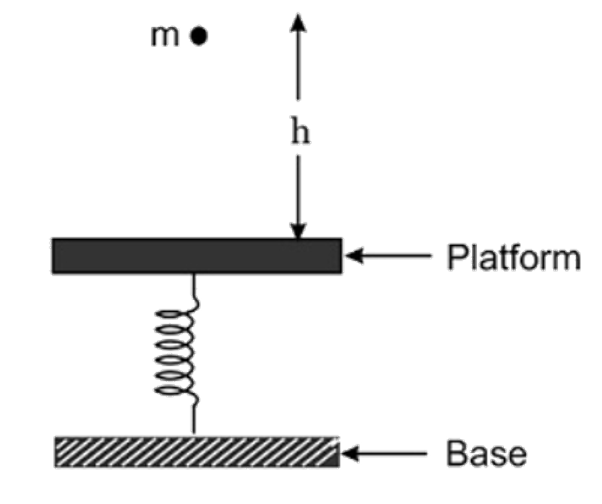
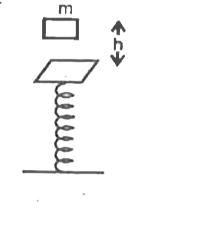
A ball of mass $m$ is droppped from a height $h$ on a platform fixed at the top of a vertical spring. The platform is depressed by a distance $x$. What is the spring constant $K$?

Options

A. `(2mg)/(x)`
B. `(2mgh)/(x^(2)`
C. `(2mg(h+x))/(x^(2)`
D. `(2mg(h+x))/(h^(2)`

Answer

C

Explanation

To find the spring constant $$K$$ when a ball of mass $$m$$ is dropped from a height $$h$$ onto a platform fixed at the top of a vertical spring, which is depressed by a distance $$x$$, we can use the principle of conservation of energy.

1. Identify the energies involved:
When the ball is dropped from height \( h \), it possesses gravitational potential energy given by:
\( PE_{\text{initial}} = mgh \)
As the ball falls, this potential energy is converted into kinetic energy and then into the potential energy of the spring when the spring is compressed by distance \( x \).

2. Calculate the total potential energy at maximum compression:
At the point of maximum compression of the spring, the total distance fallen by the ball is \( h + x \). Therefore, the gravitational potential energy at this point is:
\( PE_{\text{total}} = mg(h + x) \)

3. Calculate the potential energy stored in the spring:
The potential energy stored in the spring when it is compressed by distance \( x \) is given by:
\( PE_{\text{spring}} = \frac{1}{2} K x^2 \)

4. Apply the conservation of energy principle:
According to the conservation of energy, the total gravitational potential energy lost by the ball will equal the potential energy stored in the spring:
\( mg(h + x) = \frac{1}{2} K x^2 \)

5. Rearranging the equation to solve for \( K \):
Rearranging the equation gives:
\( K x^2 = 2mg(h + x) \)
Therefore, we can express \( K \) as:
\( K = \frac{2mg(h + x)}{x^2} \)

Final Result:
The spring constant \( K \) is given by:
\( K = \frac{2mg(h + x)}{x^2} \)