A block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant . The maximum distance through which the spring is compressed by
10 cm
1 cm
20 cm
5 cm
The correct Answer is:A
To solve the problem of finding the maximum distance through which the spring is compressed when a block of mass 2 kg is dropped from a height of 40 cm onto a spring with a force constant of 1960 N/m, we can follow these steps:
Step 1: Understand the Energy Conservation Principle
When the block is dropped, its gravitational potential energy will be converted into elastic potential energy of the spring at maximum compression.
Step 2: Write the Expressions for Potential Energies
1. Gravitational Potential Energy (GPE) when the block is at height h:
GPE=mgh
where:
- m=2kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
- h=0.4m (height in meters)
2. Elastic Potential Energy (EPE) stored in the spring when compressed by distance x:
EPE=12kx2
where:
- k=1960N/m (spring constant)
Step 3: Set Up the Energy Conservation Equation
At maximum compression, the gravitational potential energy lost will equal the elastic potential energy gained:
mgh=12kx2
Step 4: Substitute the Values
Substituting the known values into the equation:
2×9.8×0.4=12×1960×x2
Calculating the left side:
2×9.8×0.4=7.84J
So the equation becomes:
7.84=12×1960×x2
This simplifies to:
7.84=980x2
Step 5: Solve for x2
Rearranging the equation gives:
x2=7.84980
Calculating x2:
x2=0.008
Step 6: Take the Square Root to Find x
Taking the square root of both sides:
x=√0.008=0.0894m=8.94cm
Step 7: Round to the Nearest Option
The closest option to 8.94 cm is 10 cm. Therefore, the maximum distance the spring is compressed is approximately:
10cm
When the block is dropped, its gravitational potential energy will be converted into elastic potential energy of the spring at maximum compression.
1. Gravitational Potential Energy (GPE) when the block is at height h:
GPE=mgh
where:
- m=2kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
- h=0.4m (height in meters)
EPE=12kx2
where:
- k=1960N/m (spring constant)
At maximum compression, the gravitational potential energy lost will equal the elastic potential energy gained:
mgh=12kx2
Substituting the known values into the equation:
2×9.8×0.4=12×1960×x2
Calculating the left side:
2×9.8×0.4=7.84J
So the equation becomes:
7.84=12×1960×x2
This simplifies to:
7.84=980x2
Rearranging the equation gives:
x2=7.84980
Calculating x2:
x2=0.008
Taking the square root of both sides:
x=√0.008=0.0894m=8.94cm
The closest option to 8.94 cm is 10 cm. Therefore, the maximum distance the spring is compressed is approximately:
10cm
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.3
Explore 10 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:EXERCISES(TAKING IT TOGETHER)
Explore 83 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.1
Explore 20 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
Similar Questions
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA block of 2 kg is suspended from the ceiling through a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
View Solution
Knowledge Check
A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
A block A has a mass m1=2kg and is attached to a spring of spring constant 50 N/m. Another block of mass 4 kg is pressed against A, so that the spring is compressed by a distance d. Then find the maximum value of d (in metre) for which on release of B. the block A does no lose contact from wall. (Friction coefficient μ=0.5).
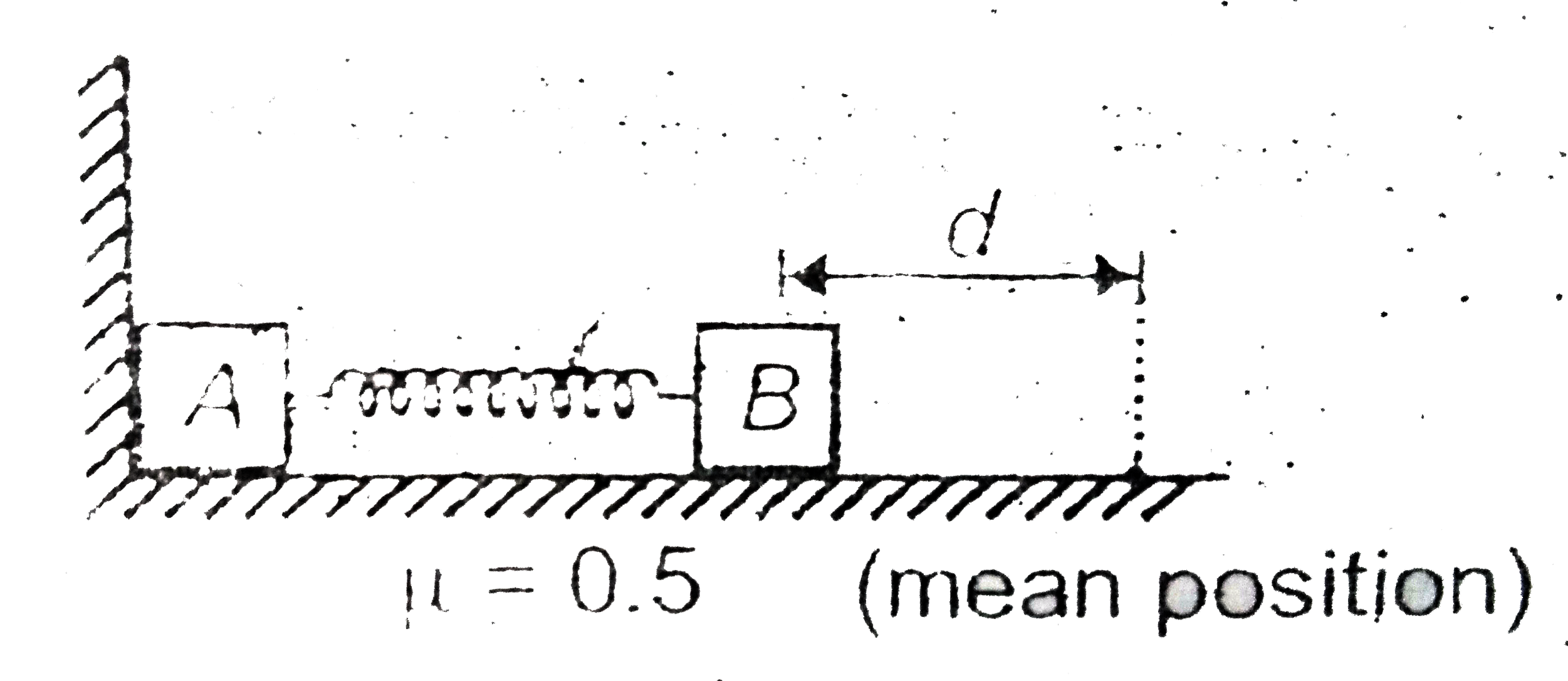
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View SolutionA block of mass 180g is suspended by a massless spring. The spring extends by 1.8cm due to the weight of block. A particle of mass 20g is dropped from a height 80cm on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
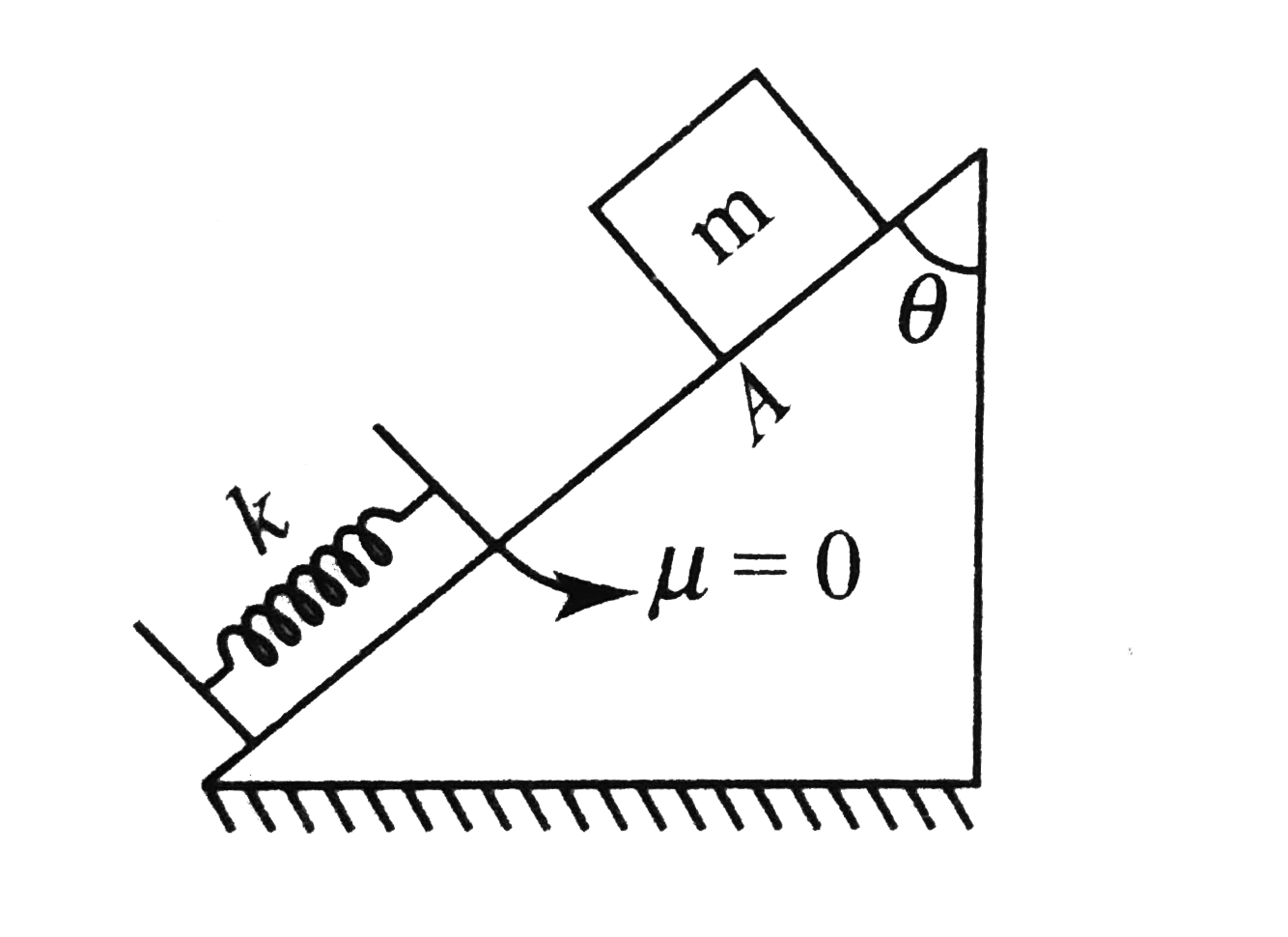
View SolutionA block of mass m is released from rest at point A. The compression in spring (force constant k) when the speed of block is maximum is found to be nmgcosθ4k. What should be the value of n?
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
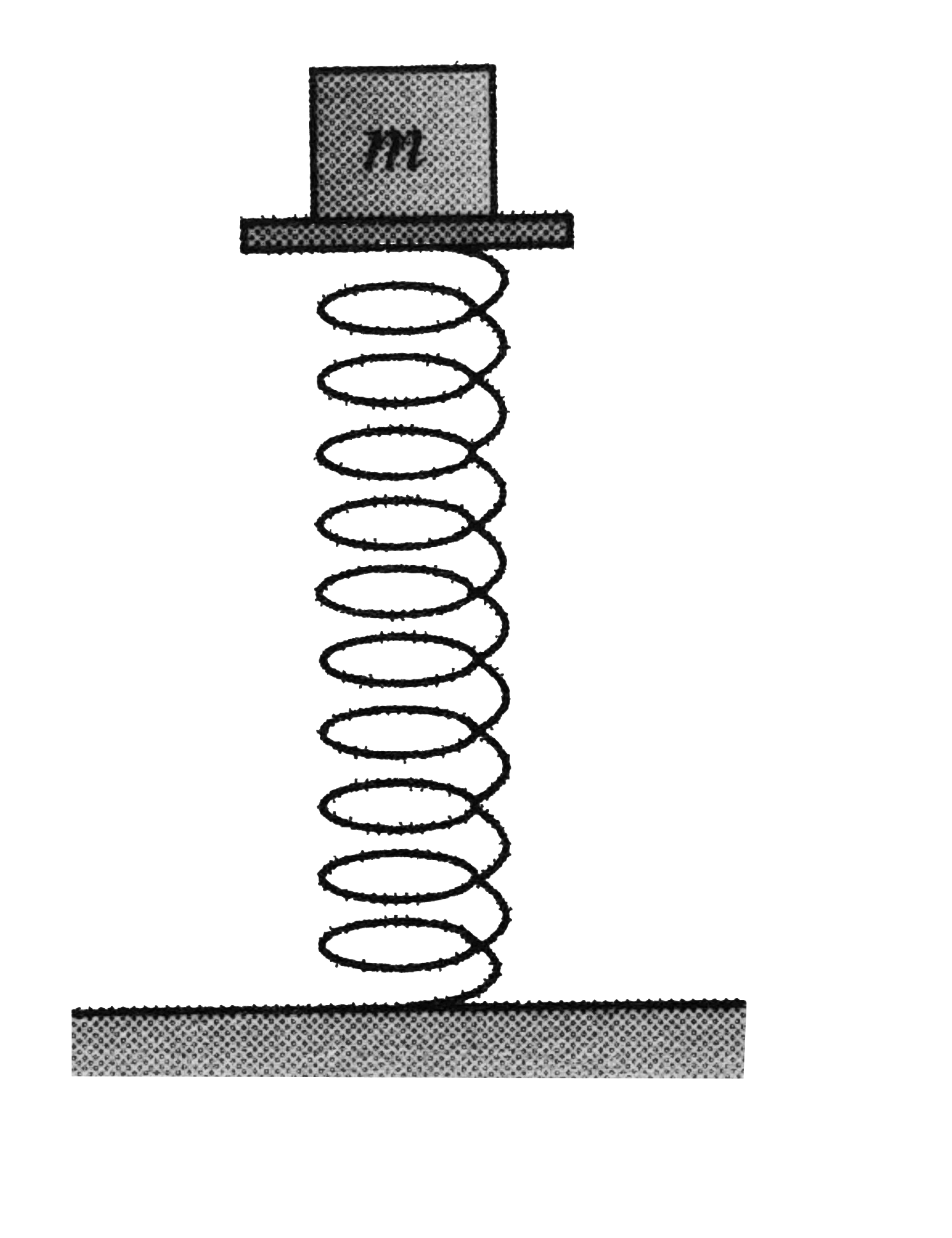
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View Solution

