A mass of 1 kg is acted upon by a single force F=(4ˆi+4ˆj)N. Under this force it is displaced from (0,0) to (1m,1m). If initially the speed of the particle was 2 ms−1, its final speed should be
6ms−1
4.5ms−1
8ms−1
4ms−1
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Mass (m) = 1 kg
- Force (F) = 4^i+4^j N
- Initial speed (V_i) = 2 m/s
- Initial position = (0,0)
- Final position = (1,1)
Step 2: Calculate the displacement vector
The displacement vector →S can be calculated as:
→S=Final position−Initial position=(1,1)−(0,0)=1^i+1^j
Step 3: Calculate the work done by the force
The work done W by the force is given by the dot product of the force and the displacement:
W=→F⋅→S=(4^i+4^j)⋅(1^i+1^j)
Calculating the dot product:
W=4⋅1+4⋅1=4+4=8 J
Step 4: Use the work-energy theorem
According to the work-energy theorem:
W=ΔKE=KEf−KEi
Where:
- KEf=12mV2f (final kinetic energy)
- KEi=12mV2i (initial kinetic energy)
Substituting the values:
8=12⋅1⋅V2f−12⋅1⋅(2)2
This simplifies to:
8=12V2f−2
Step 5: Solve for V2f
Rearranging the equation:
8+2=12V2f
10=12V2f
Multiplying both sides by 2:
20=V2f
Step 6: Find Vf
Taking the square root:
Vf=√20≈4.47 m/s
Step 7: Round to the nearest option
Since the closest option provided is 4.5 m/s, we conclude:
Final speed Vf≈4.5 m/s
Final Answer
The final speed of the particle is approximately 4.5 m/s.
---
- Mass (m) = 1 kg
- Force (F) = 4^i+4^j N
- Initial speed (V_i) = 2 m/s
- Initial position = (0,0)
- Final position = (1,1)
The displacement vector →S can be calculated as:
→S=Final position−Initial position=(1,1)−(0,0)=1^i+1^j
The work done W by the force is given by the dot product of the force and the displacement:
W=→F⋅→S=(4^i+4^j)⋅(1^i+1^j)
Calculating the dot product:
W=4⋅1+4⋅1=4+4=8 J
According to the work-energy theorem:
W=ΔKE=KEf−KEi
Where:
- KEf=12mV2f (final kinetic energy)
- KEi=12mV2i (initial kinetic energy)
8=12⋅1⋅V2f−12⋅1⋅(2)2
This simplifies to:
8=12V2f−2
Rearranging the equation:
8+2=12V2f
10=12V2f
Multiplying both sides by 2:
20=V2f
Taking the square root:
Vf=√20≈4.47 m/s
Since the closest option provided is 4.5 m/s, we conclude:
Final speed Vf≈4.5 m/s
The final speed of the particle is approximately 4.5 m/s.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.3
Explore 10 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:EXERCISES(TAKING IT TOGETHER)
Explore 83 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.1
Explore 20 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
Similar Questions
A constant force F=(ˆi+3ˆj+4ˆk)N acts on a particle and displace it from (-1m,2m,1m)to(2m,-3m,1m).
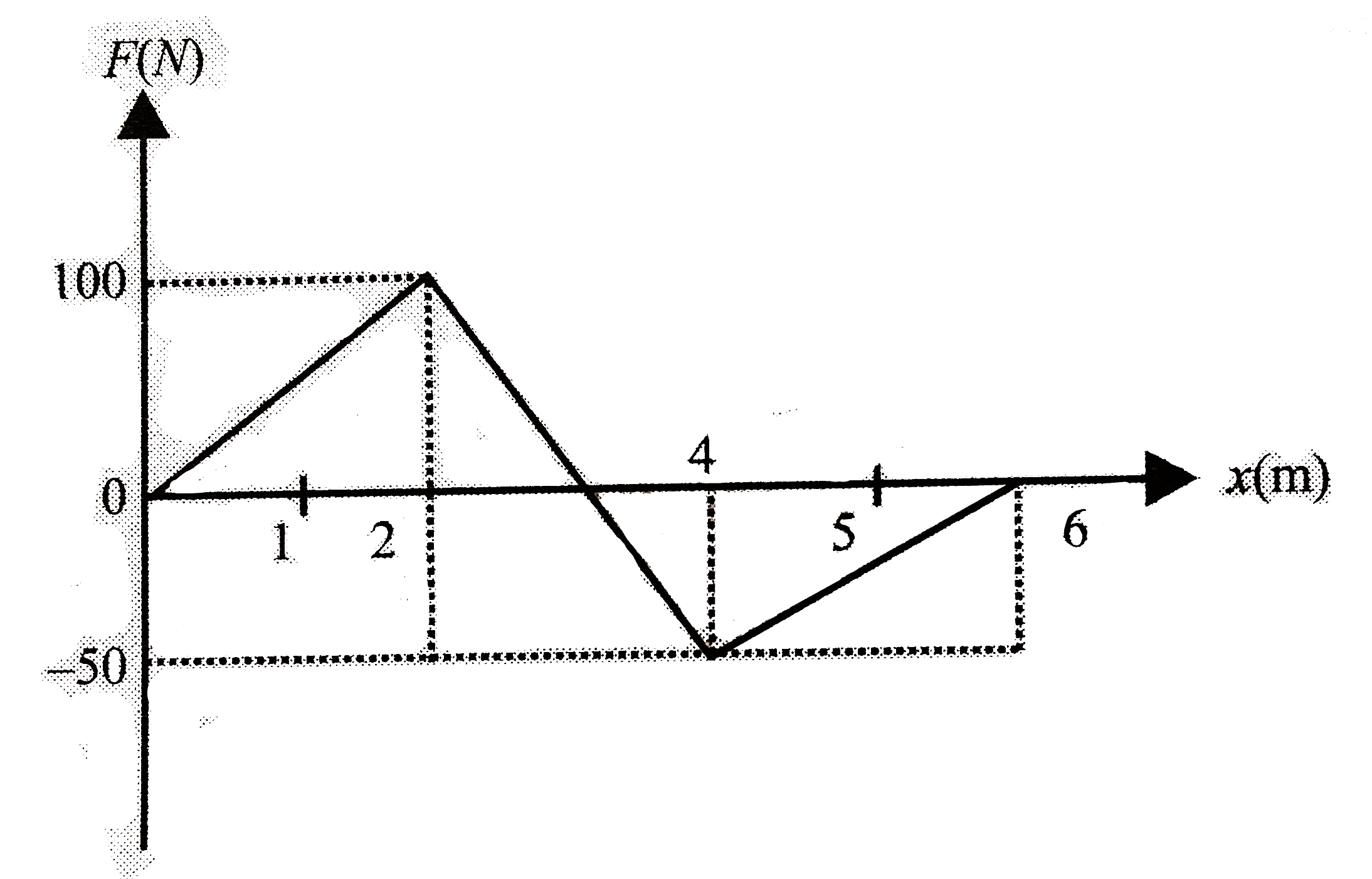
View SolutionA stationary particle of mass m=1.5kg is acted upon by a variable force. The variation of force with respect to displacement is plotted in figure.
a. Calculate the velocity acquired by the particle after getting displaced through 6m.
b. What is the maximum speed attained by the particle and at what time is it attained?
View SolutionA particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionA body of mass 2 kg is acted upon by two forces →D1=(2ˆi+3ˆj)Nand→F2(−2ˆk+3ˆj)N. If the body is displaced from A(3m,−2m,1m) to B (−1m,+2m,−3m), then work done on the body is
View SolutionThe average resisting force that must act on 5kg mass to reduce its speed from 65 to 15ms−1 in 2s is
View SolutionA body of mass 2 kg is acted upon by two forces 2 N and 5 N in the direction ofˆi+ˆj and ˆj−ˆk respectively. If the body is displaced from (3,-2, 1) to (-1, 2, 3) (Positions are in m), then work done is
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass 0.5 kg is subjected to a force which varies with distance as shown in figure

1. The work done by the force during the displacement from x=0 to x=4andx=4 to x=12are respectively
(1)20J,40J(2)40J,40J(3)20J,60J(4)40J,80J
2. The increaase in kinetic energy of the particle during its displac ement from x=0 to x=12 m is
(1)20J(2)40J(3)80J(4)120J
3. If the speed of the particle at x=0 is 4 m/s, its speed st x=8 m is
(1)8m/s(2)16m/s(3)32m/s(4)4m/s
View SolutionA body is displaced from (0,0) to (1m,1m) along the path x=y by a force F=(x2ˆj+yˆi)N. The work done by this force will be
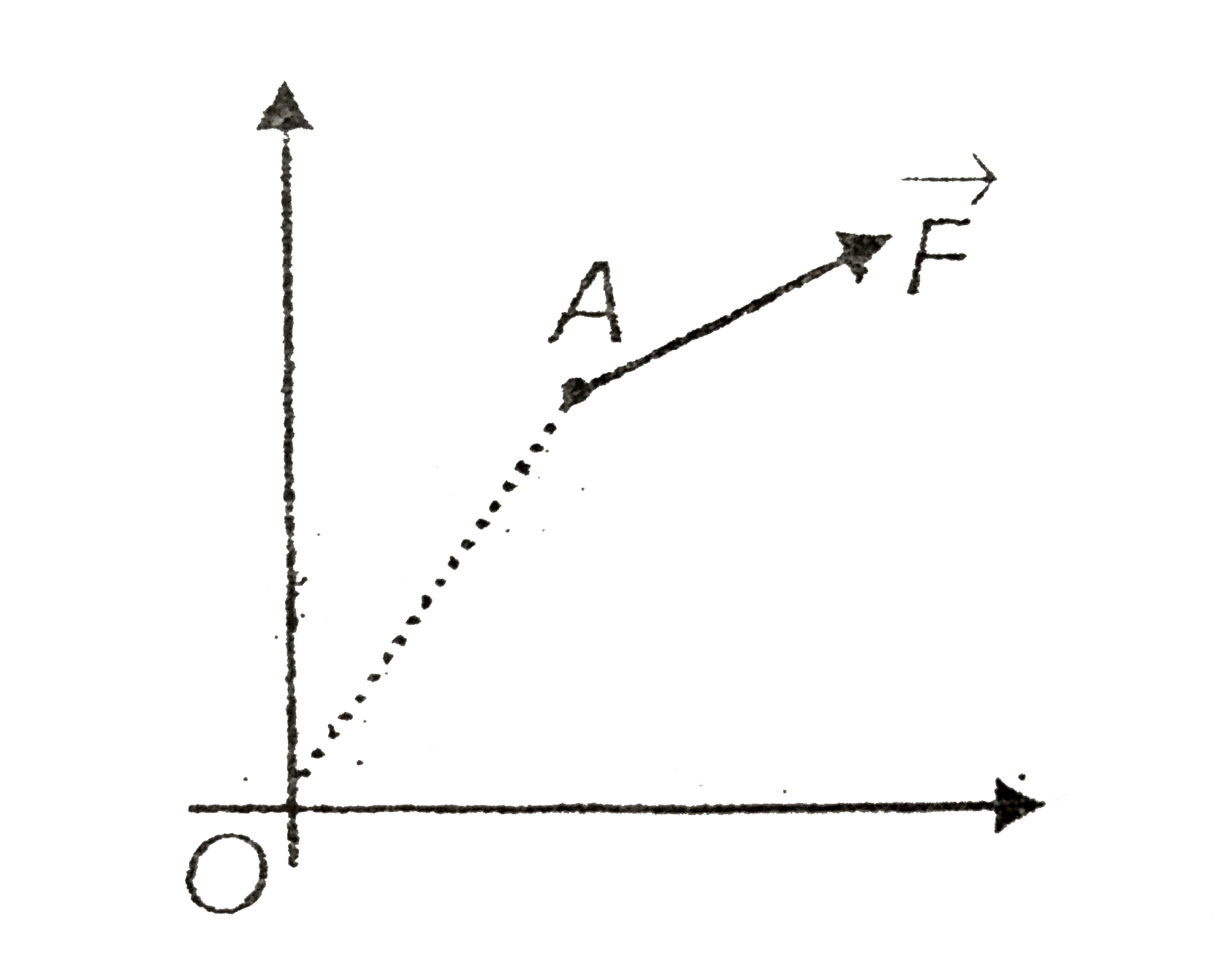
View SolutionA force →F=(3ˆi+4ˆj)N is acting on a point mass m=(12)kg at a point A(2m,2m). Find the angular acceleration of the line OA at this instant.
View Solution

