A ball of mass $m$ is attached to the lower end of a light vertical spring of force constant $K$ . The upper end of the spring is fixed. The ball is released from rest with the spring at its normal $($ unstretched $)$ length, and comed to rest again after descending through a distance $x$ .

A

$x = \frac{m g}{k}$

B

$x = \frac{2 m g}{k}$

C

the ball will have no acceleration at the position where it has descended through $\frac{x}{2}$

D

the ball will have an upward acceleration equal to $g$ at its lowermost position.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C, D

initial velocity $=$ final velocity = 0 from energy conservation
$m g x - \frac{1}{2} k x^{2} = 0$
$x = \frac{2 m g}{k}$ ,
at descended length $= \frac{x}{2}$
$\frac{k x}{2} = k . \frac{2 m g}{2 k} = m g$
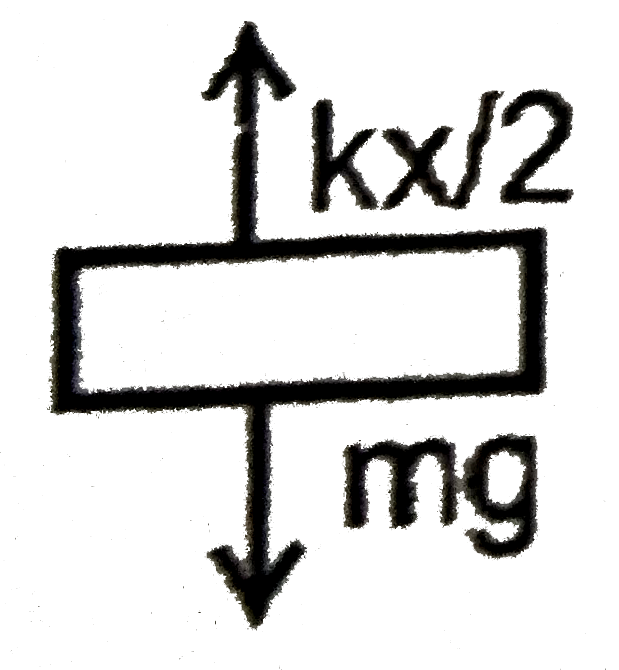
Net force $= 0$
$\Rightarrow a = 0$ at lower most position.

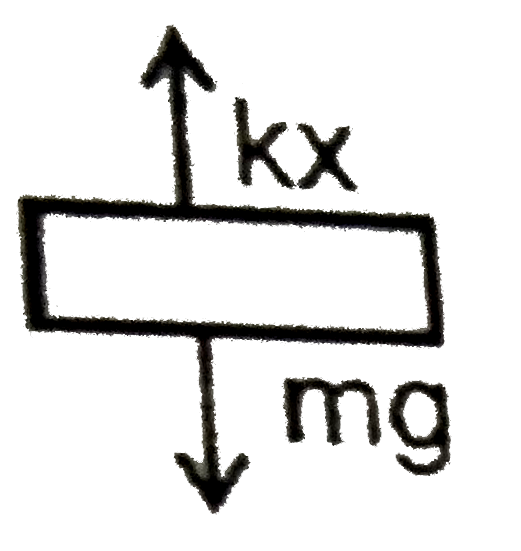
force $= K x - m g = K \frac{2 m g}{K} - m g = m g$
$\Rightarrow a = g ↑$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two blocks of masses $m_{1}$ and $m_{2}$ are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block $(m_{2})$ drops off. The other block $(m_{1})$ will

Aremain undistrubed
Bmove through a distance $\frac{m_{2} g}{k}$ and come to rest
Cundergo vertical SHM with a time period of $2 π \sqrt{\frac{m_{1}}{k}}$
Dundergo vertical SHM with a time period of
$2 π \sqrt{\frac{m_{1} + m_{2}}{k}}$
Question 2 - Select One or More
A mass of $0.2 k g$ is attached to the lower end of a massless spring of force-constant $200 N / m$ , the upper end of which is fixed to a rigid support. Which of the following statements $i s / a r e$ true?
AIn equilibrium, the spring will be stretched by $1 c m$ .
BIf the mass is raised till the spring is unstreched state and then released, it will godown by $2 c m$ before moving upwards.
CThe frequency of oscillation will be nearly $5 H z$ .
DIf the system is taken to the moon, the frequency of oscillation will be the same as on the earth.
Question 3 - Select One

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
A $m g h = \frac{1}{2} k x^{2}$
B $m g (h + x) = \frac{1}{2} k x^{2}$
C $m g h = \frac{1}{2} k {(x + h)}^{2}$
D $m g (h + x) = \frac{1}{2} k {(x + h)}^{2}$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 63

Home
Ask Doubt
Profile