A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
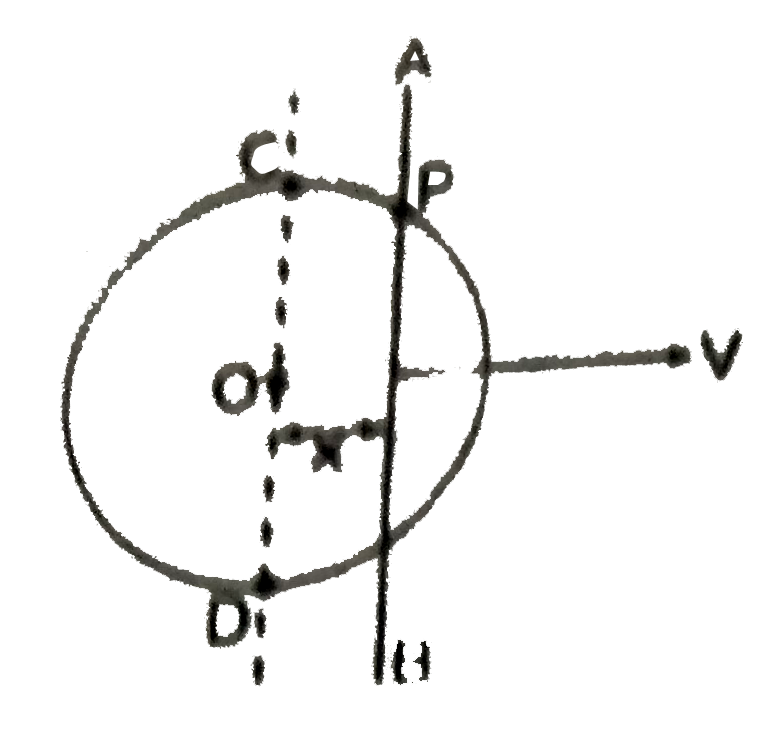
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
The correct Answer is:(a)p=54V(v)Vcosecθ
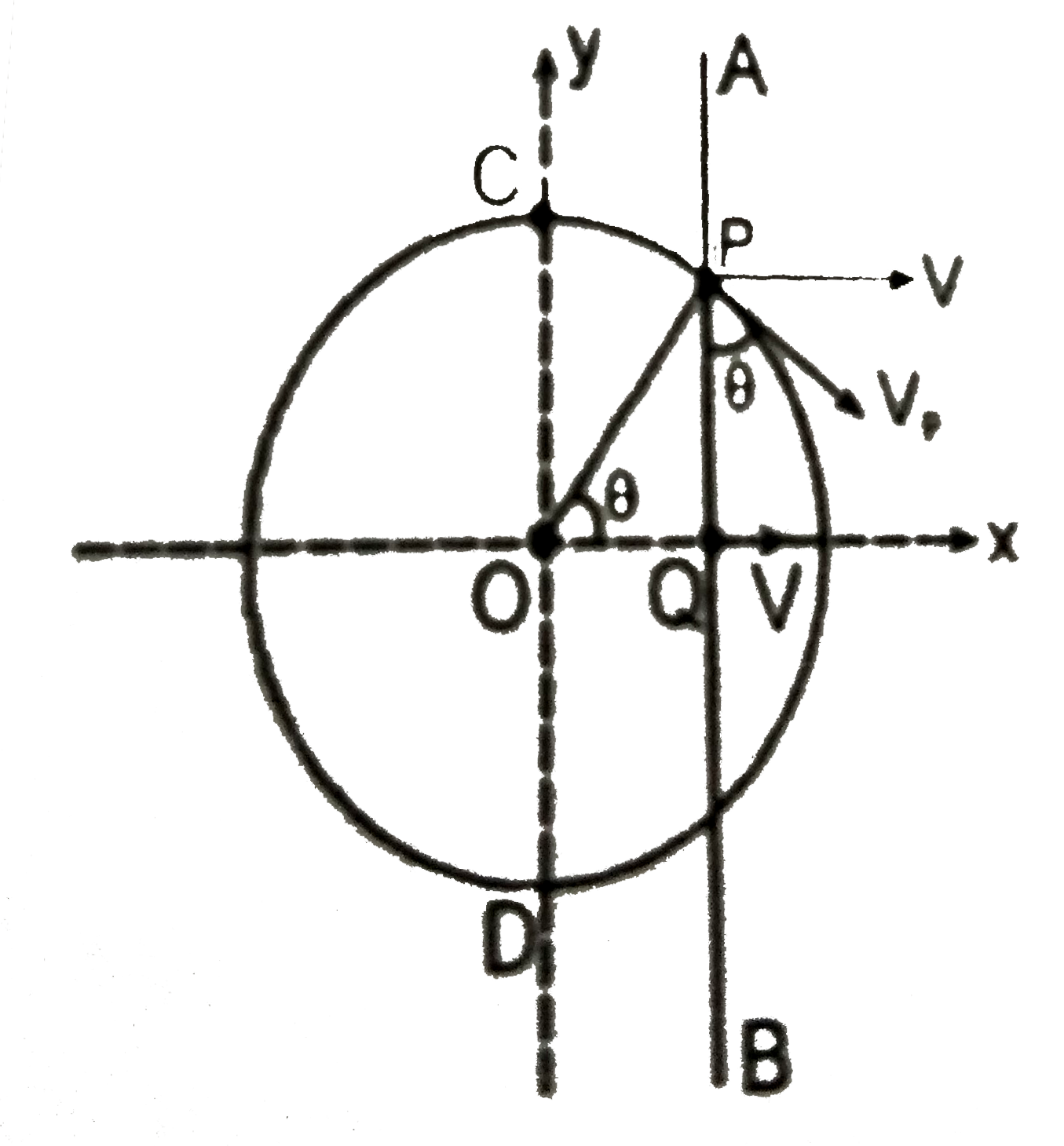
As a rod AB moves, the point 'P' will always lies on the circle.
∴Its velcoity will be along the circle as shown by 'VP' in the figure. If the point P has to lie on the rod 'AB' also then it should have component in 'x' direction as 'V'
∴VPsinθ=V
⇒Vp=Vcosecθ
herecosθ=xR=1R.3R5=35
....Ans.
ω=VPR=5V4R
ALTERNATE SOLUTION :
Sol. (a) Let 'P' have coordinate (x,y)
x=Rcosθ,y=Rsinθ
Vx=dxdt=−Rsinθdθdt=V⇒dθdt=−VRsinθ
Vy=Rcosθdθdt=Rcosθ(−VRsinθ)
=−Vcotθ
∴VP=√V2x+V2y=√V2+V2cot2θ
=Vcosecθ....Ans.
Sol.(b)ω=VPR=5V4R
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 64
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 65
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 62
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
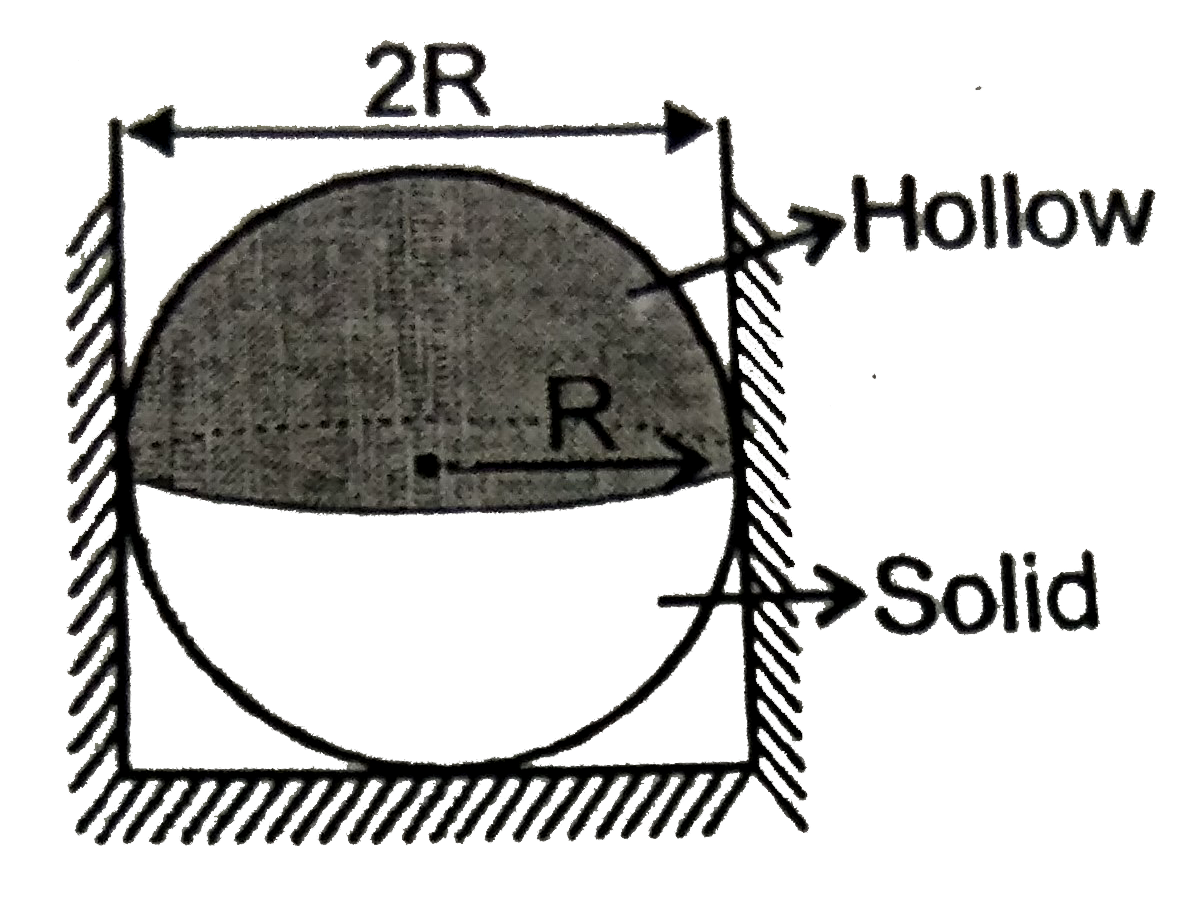
A compound sphere is made by joining a hemispherical shell and a solid hemisphere of same radius R and same mass as shown in figure. This system is kept between two smooth parallel walls and a smooth floor with the hollow hemisphere on the top as shown in figure. The maximum angular velocity of the compound shere when the system is slightly disturbed is ( all surfaces are smooth )
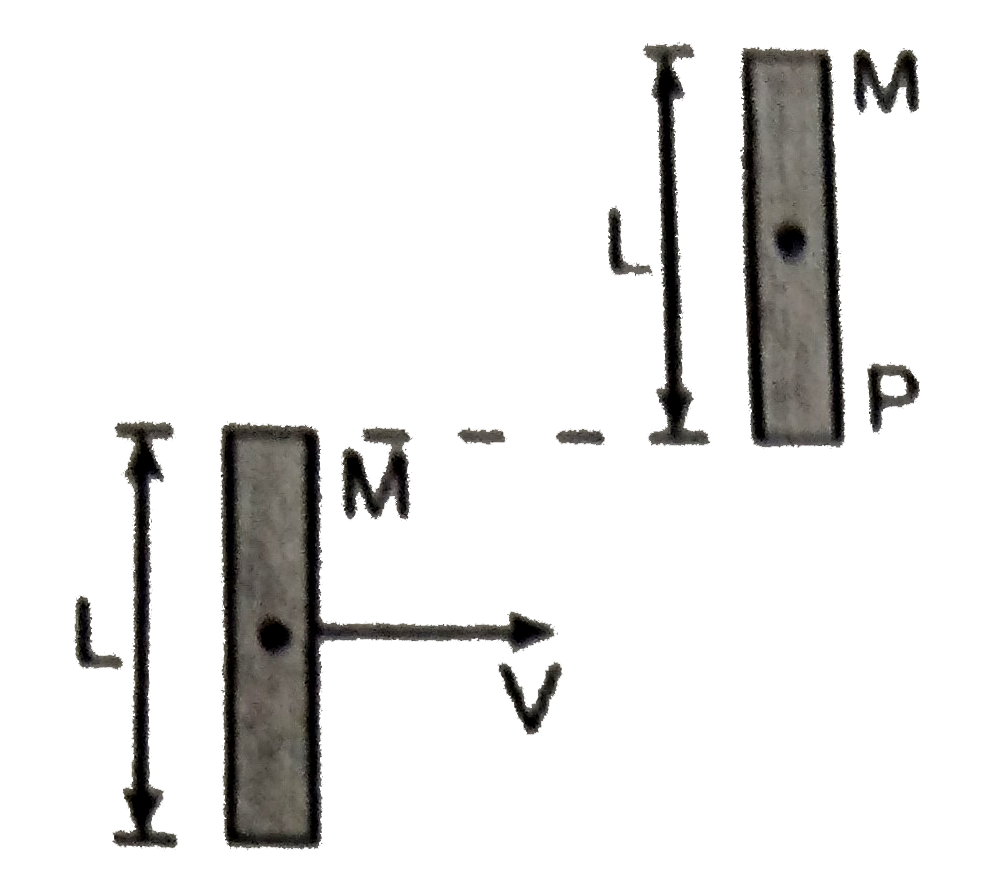
View SolutionA bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L). The angular velocity of the composite bar will be
View SolutionIn which of the following cases the friction force between 'A' and 'B' is maximum. In all cases μ1=0.5,μ2=0.
View SolutionSpecific resistance of a wire depends on its
View SolutionA wire loaded by a weight of density 7.6gcm−3 is found to measure 90cm. On immersing the weight in water, the length decreases by 0.18cm. Find the original length of wire.
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2 ms^-1 towards right. The velocity of end B of rod at the instant shown in figure is
View SolutionA rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity m/s towards right. The velocity of end B of rod when rod makes an angle of 60^@ with ground is :
View SolutionTwo points of a rod move with velocity 3 v and v perpendicular to the rod and in the same direction. Separated by a distance r . Then the angular velocity of the rod is :
View SolutionA rod AB is moving on a fixed circle of radius R=5m with constant velocity v=4m//s as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=(3R)/5 from center of the circle. The velocity of the rodf is perpendicular to its lenght and the rod is always paraller to the diameter (CD) Speed of point of intersection P is
View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
View SolutionIn the figure shown a smooth ring is connected to rod AB, while rod CD passes through ring. At the given instant angular velocity of rod AB about hinge A is 1 rod/s and AC=CB. Instantaneous angular velocity of rod CD about hinge C is
View SolutionFind the velocity of the moving rod at time t if the initial velocity of the rod is v and a constant force F is applied on the rod. Neglect the resistance of the rod.
View Solutionएक धातु की छड़ नियत वेग से लम्बाई के लम्बवत गति करती है छड़ ऐसे चुम्बकीय क्षेत्र में गति करती है जो कि छड़ और वेग दोनों के लम्बवत है । सही कथन चुनिए
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2 ms^-1 towards right. The velocity of end B of rod at the instant shown in figure is
View Solution

