A rod AB is moving on a fixed circle of radius R=5m with constant velocity v=4m/s as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from center of the circle. The velocity of the rodf is perpendicular to its lenght and the rod is always paraller to the diameter (CD)
Speed of point of intersection P is

Let P have co-ordiantes (x,y)
x=Rcosθ,y=Rsinθ
Vx=Rsinθdθdt,dθdt=−vRsinθ
Vy=Rcosθdθdt=Rcosθ(−vRsinθ)
=−vcotθ
vp=√v2x+v2y
Topper's Solved these Questions
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:IIT QUES.
Explore 4 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL I(H.W)
Explore 43 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL-VI PASSAGE
Explore 3 Videos
- CALORIMETRYBook:NARAYNAChapter:CALORIMETRYExercise:Level- II (H.W)
Explore 11 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
Similar Questions
A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
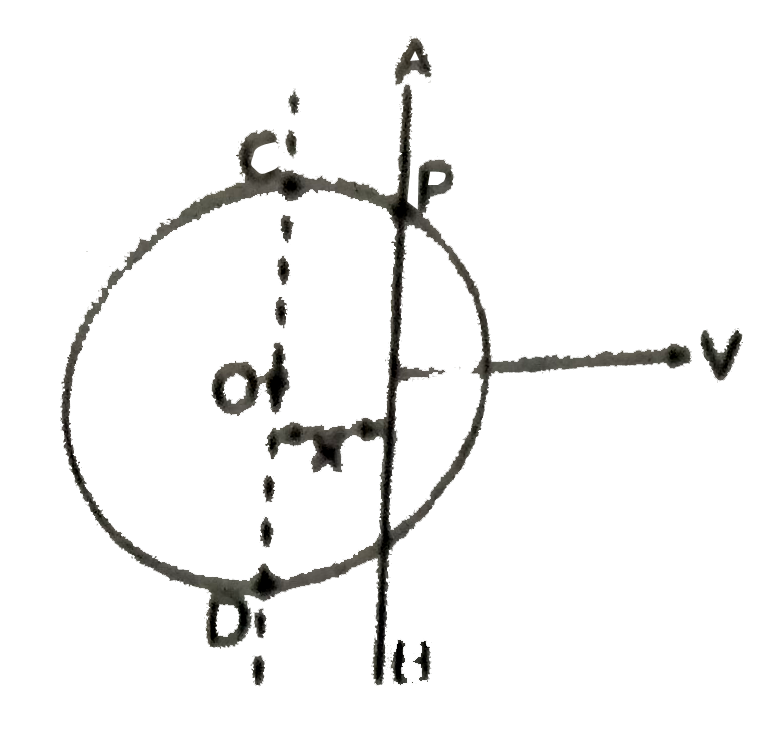
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
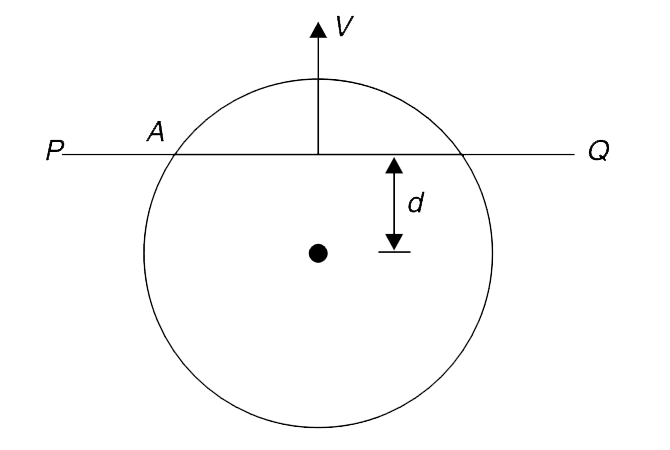
View Solution(a) A line PQ is moving on a fixed circle of radius R. The line has a constant velocity v perpendicular to itself. Find the speed of point of intersection (A) of the line with the circle at the moment the line is at a distance d=R/2 from the centre of the circle.
(b) In the figure shown a pin P is confined to move in a fixed circular slot of radius R. The pin is also constrained to remains inside the slot in a straight arm O'A. The arm moves with a constant angular speed w about the hinge O'. What is the acceleration of point P ?
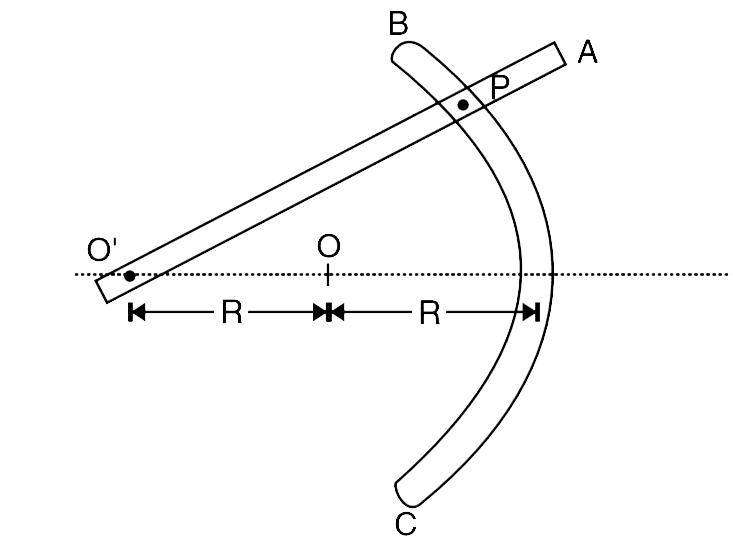
View Solution
Knowledge Check
A particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
 A2vcos40∘B2vsin20∘C2vcos20∘Dnone of these
A2vcos40∘B2vsin20∘C2vcos20∘Dnone of theseEnd A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate

the velocity of the CM of the rodA57v0 at tan−143 below horizontalB57v0 at tan−134 below horizontalC56v0 at tan−134 below horizontalD56v0 at tan−143 below horizontalTwo points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction, separated by a distance r. Then the angular velocity of the rod is :
A3vrB4vrC5vrD2vr
Find the velocity of the moving rod at time t if the initial velocity of the rod is v and a constant force F is applied on the rod. Neglect the resistance of the rod.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be

View SolutionIn the figure shown the instantaneous speed of end A of the rod is v to the left the angular velocity of the rod of lengthL must be

View Solution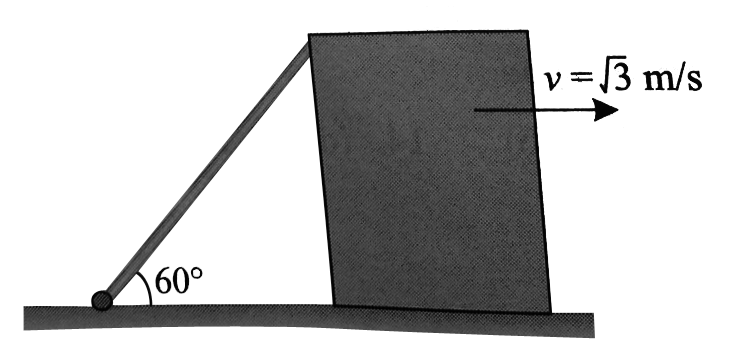
A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity m/s towards right. The velocity of end B of rod when rod makes an angle of 60∘ with ground is :
View Solution

