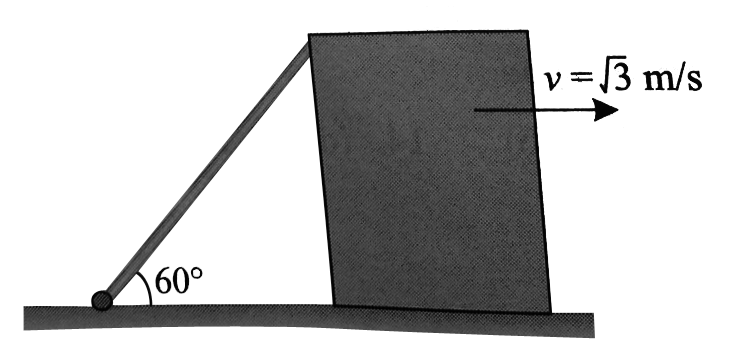
A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity $\sqrt{3}$ m/s towards right. The velocity of end B of rod when rod makes an angle of $60^{\circ}$ with ground is :

$\sqrt{3} \frac{m}{s}$

$2 \frac{m}{s}$

$2 \sqrt{3} \frac{m}{s}$

$3 \frac{m}{s}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $A B = l$ , $B = (x, y)$
${\to v}_{B} = v_{x} ˆ i + v_{y} ˆ j$
${\to v}_{B} = \sqrt{3} ˆ i + v_{y} ˆ j$
$x^{2} + y^{2} = l^{2}$
$2 x v_{x} = 2 y v_{y} = 0$
$\Rightarrow \sqrt{3} + \frac{y}{x} v_{y} = 0$
$\Rightarrow \sqrt{3} + ({tan 60}^{\circ}) v_{y} = 0$
Hence from 9i)
${\to v}_{B} = \sqrt{3} ˆ i - ˆ j$
Hence $v_{b} = 2 \frac{m}{s}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

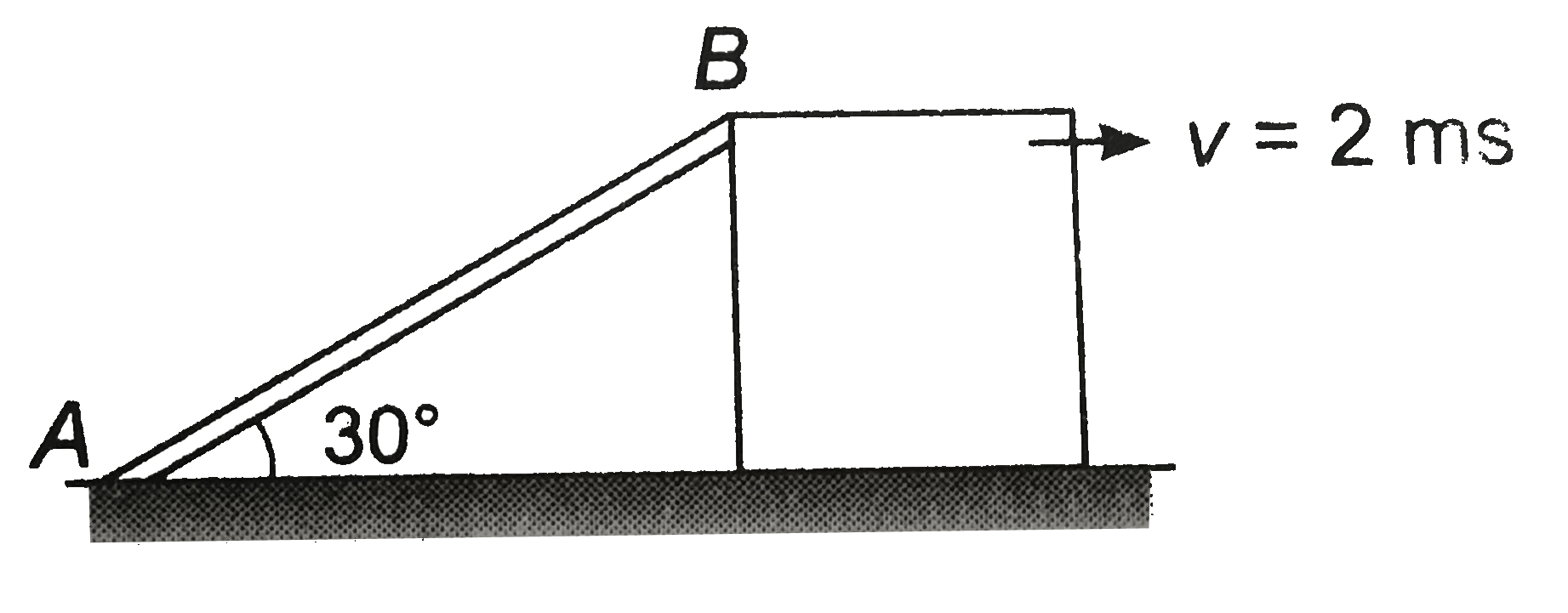
A rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity $2 m s^{- 1}$ towards right. The velocity of end B of rod at the instant shown in figure is

View Solution
A rod $A B$ of mass $M$ and length $L$ is shown in figure. End $A$ of rod is hinged and end $B$ is lying on the ground. Find the Normal reaction by ground on the rod

View Solution
A rod $A B$ of mass $M$ and length $L$ is shown in figure. End $A$ of rod is hinged and end $B$ is lying on the ground. Find the Horizontal component of the force applied by the hinge

View Solution
Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle $θ$ with the horizontal.

View Solution
A rod of length 'l' is inclined at an angle $' θ'$ with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity $v_{1}$ , what is the velocity of end B at the instant when rod makes $' θ'$ angle with the horizontal.
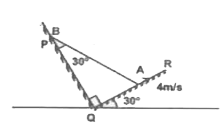
View Solution
A rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is $4 m / s$ along the wall. Find the velocity of end B, when end B makes $30^{\circ}$ with wall PQ.

View Solution
A rod $A B$ of mass $M$ and length $L$ is shown in figure. End $A$ of rod is hinged and end $B$ is lying on the ground. Find the Vertical component of the force applied by the hinge

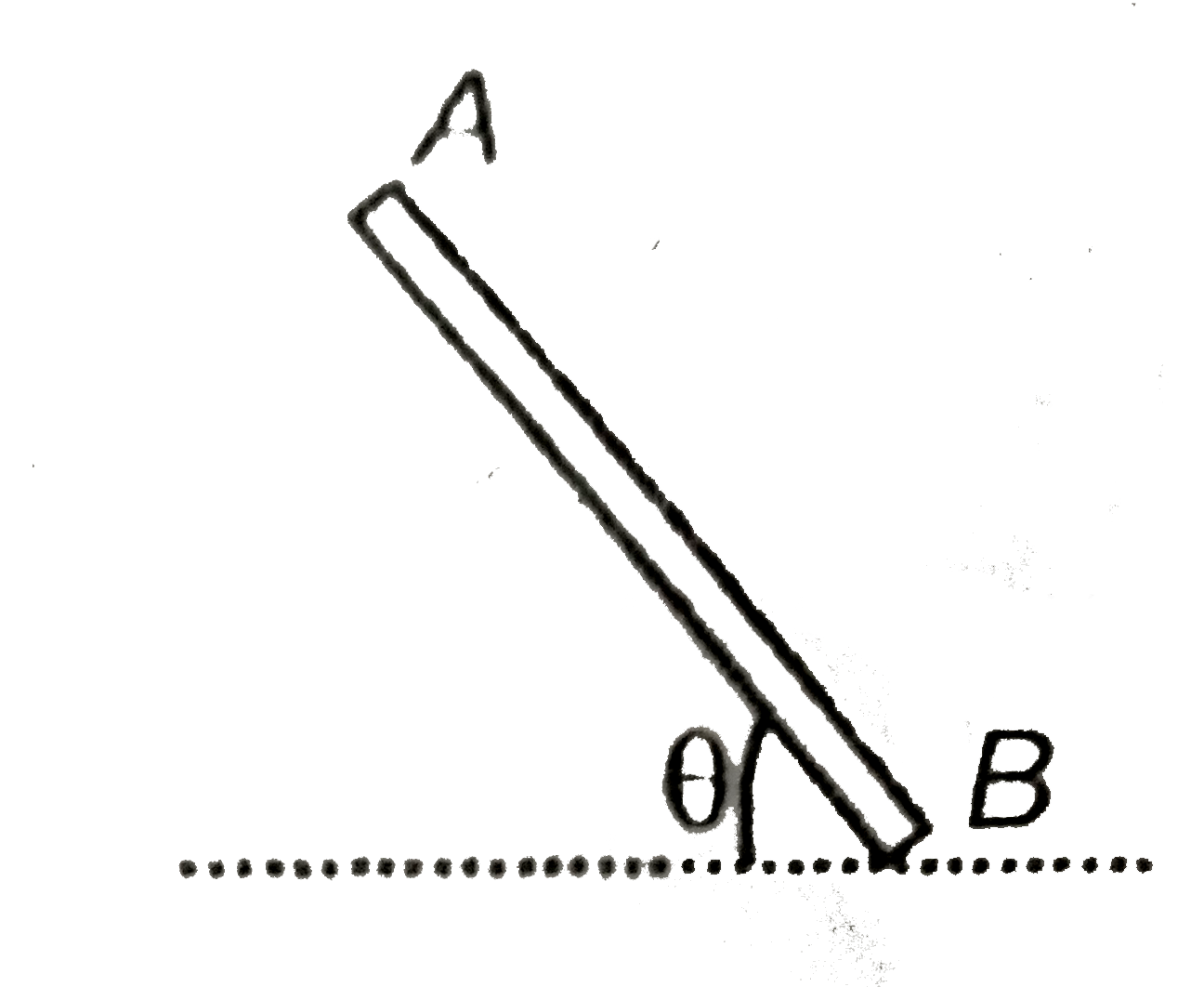
Vertical component of the force applied by the hinge
View Solution
The velocity of point A on the rod is $2 m s^{- 1}$ (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View Solution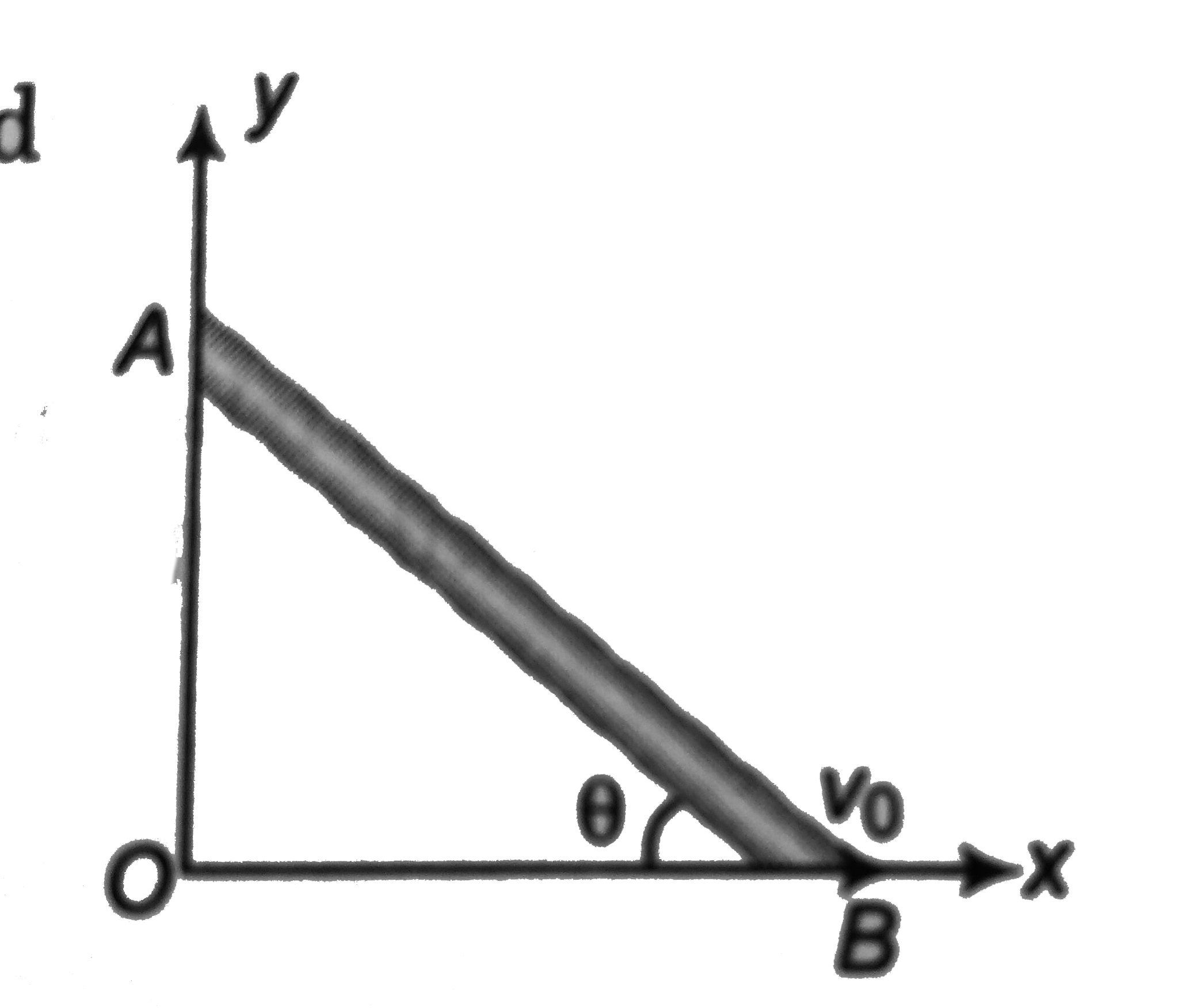
The end B of the rod AB which makes angle $θ$ with the floor is being pulled with a constant velocity $v_{v}$ as shown. The length of the rod is $l$ .
View Solution
A rod $A B$ of length $2 m$ moves in horizontal $x - y$ plane. At any instant end a of the rod is at origin and has velocity ${\to v}_{A} = 2 ˆ i + v_{y} ˆ j$ . The other end $B$ at the same instant is moving with velocity ${\to v}_{B} = 3 ˆ i + 6 ˆ j$ . The rod makes an angle of $30^{\circ}$ with the $x -$ axis at this instant (see figure)
The magnitude of angular velocity of the rod is

View Solution

A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity √3 m/s towards right. The velocity of end B of rod when rod makes an angle of 60∘ with ground is :

The correct Answer is:B

Let AB=l,B=(x,y) →vB=vxˆi+vyˆj →vB=√3ˆi+vyˆj x2+y2=l2 2xvx=2yvy=0 ⇒√3+yxvy=0 ⇒√3+(tan60∘)vy=0 Hence from 9i) →vB=√3ˆi−ˆj Hence vb=2ms

Similar Questions

Recommended Questions

A rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity $\sqrt{3}$ m/s towards right. The velocity of end B of rod when rod makes an angle of $60^{\circ}$ with ground is :