A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
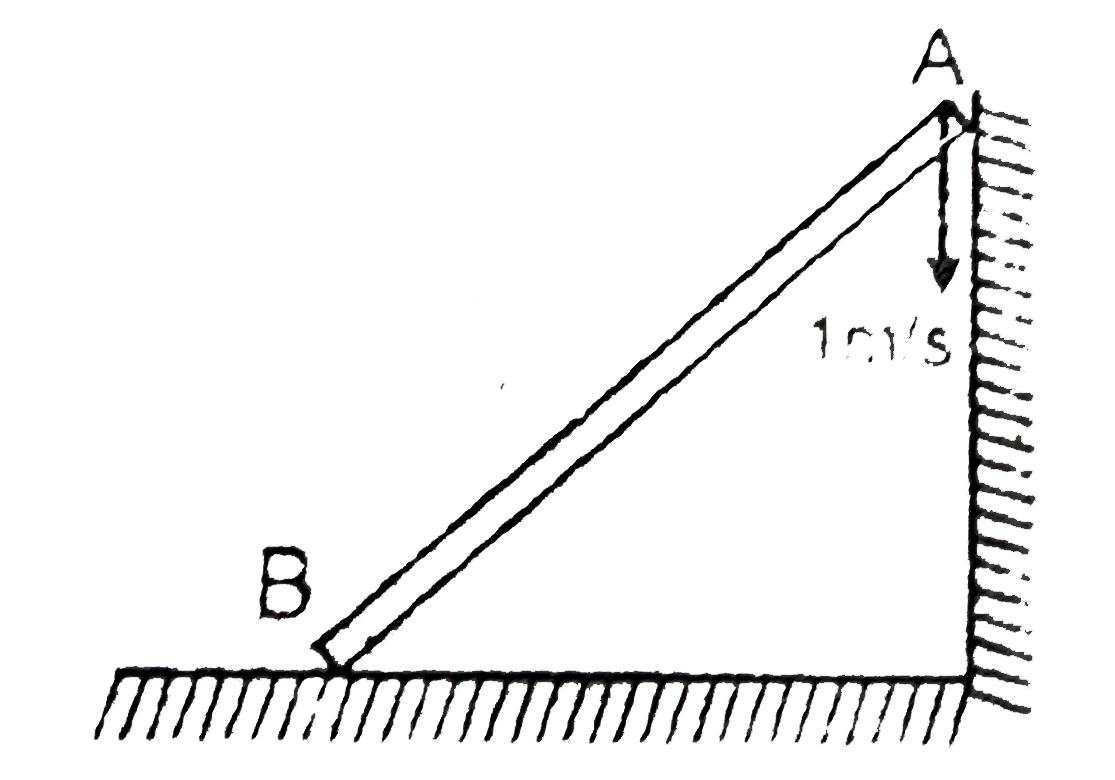
2 rad/s
1.5 rad/s
0.5 rad/s
0.75 rad/s
The correct Answer is:A
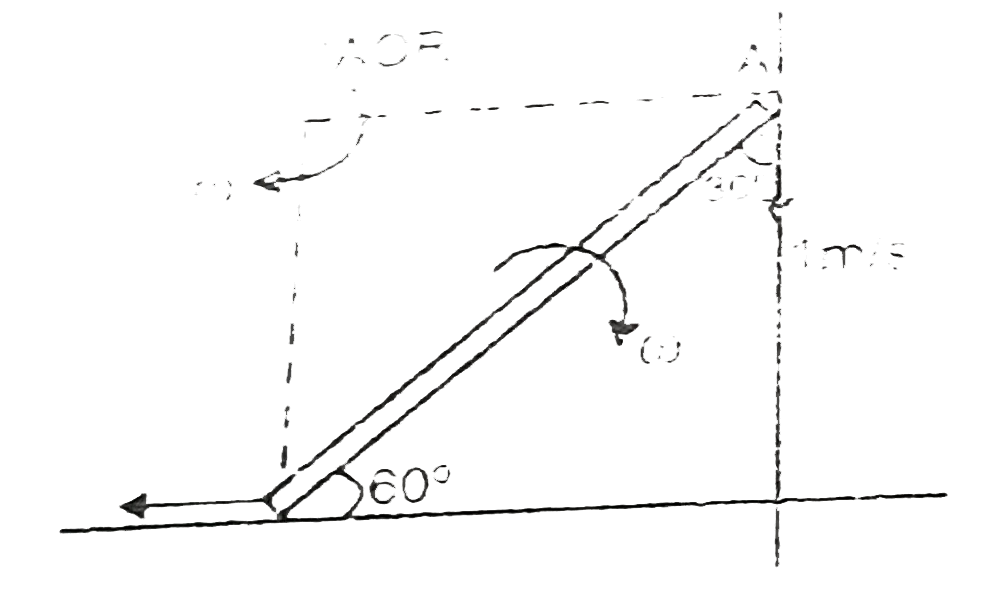
1=(1cos60∘)ω
ω=2rad/s
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.62
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.63
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.60
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
There is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
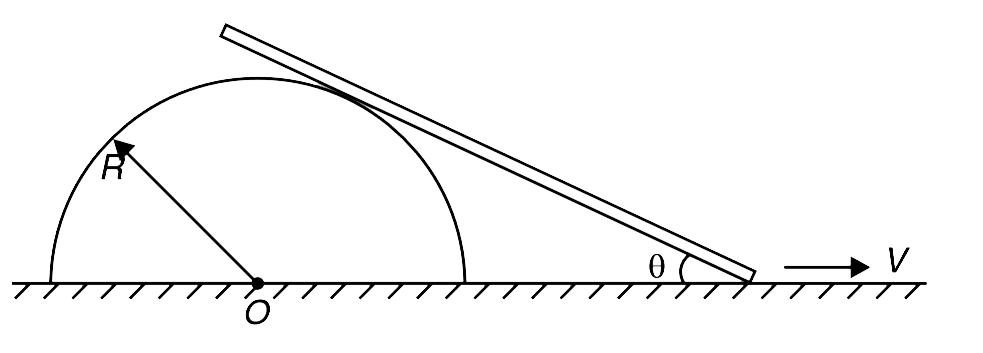
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
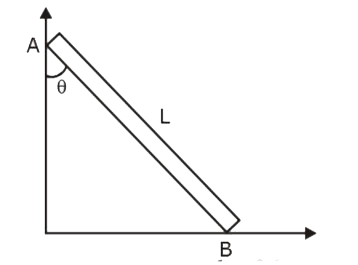
View SolutionA rod AB of length L slides in the XY plane. If the rod makes an angle θ with the vertical, the angular velocity of the rod can be found by an expression which is
View Solution
Knowledge Check
A rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
A2ms−1B1ms−1C4ms−1D1.5ms−1A rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
Av0cotθBv0cosθCv0sinθDv0tanθIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of these
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA smooth rod OP is fixed vertically. A disc of mass m and radius R is rolling without slipping at the given instant on a rough horizontal surface as shown. Velocity of centre of mass C of disc is v0. A rod AB of length L is connected with disc at A, R/2 distance vertically up from centre of disc with pin joint (about which it can rotate freely), other end of the rod is attached to a small smooth ring B, which can move freely over rod OP. At an instant rod AB makes an angle 60∘ with the vertical. The velocity of ring on the vertical rod at this instant is.
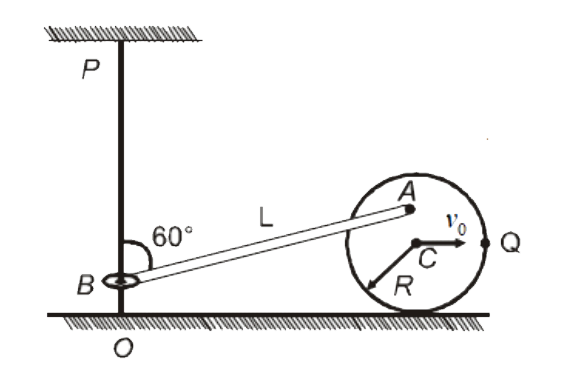
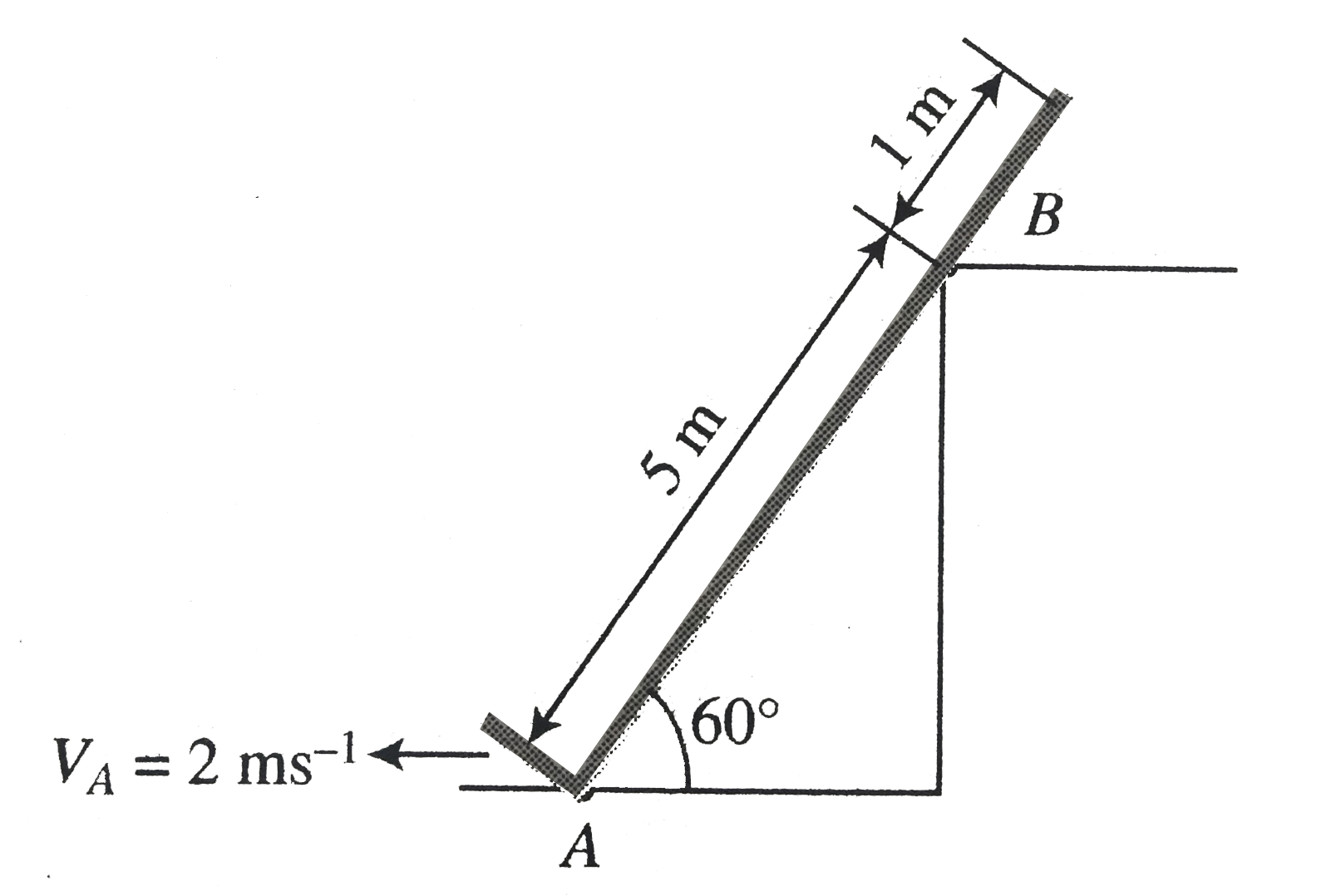
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
View SolutionEnd A of a rod AB is being pulled on the floor with a constant velocity v0 as shown. Taking the length of the rod as l, at an instant when the rod makes an angle 37∘ with the horizontal, calculate
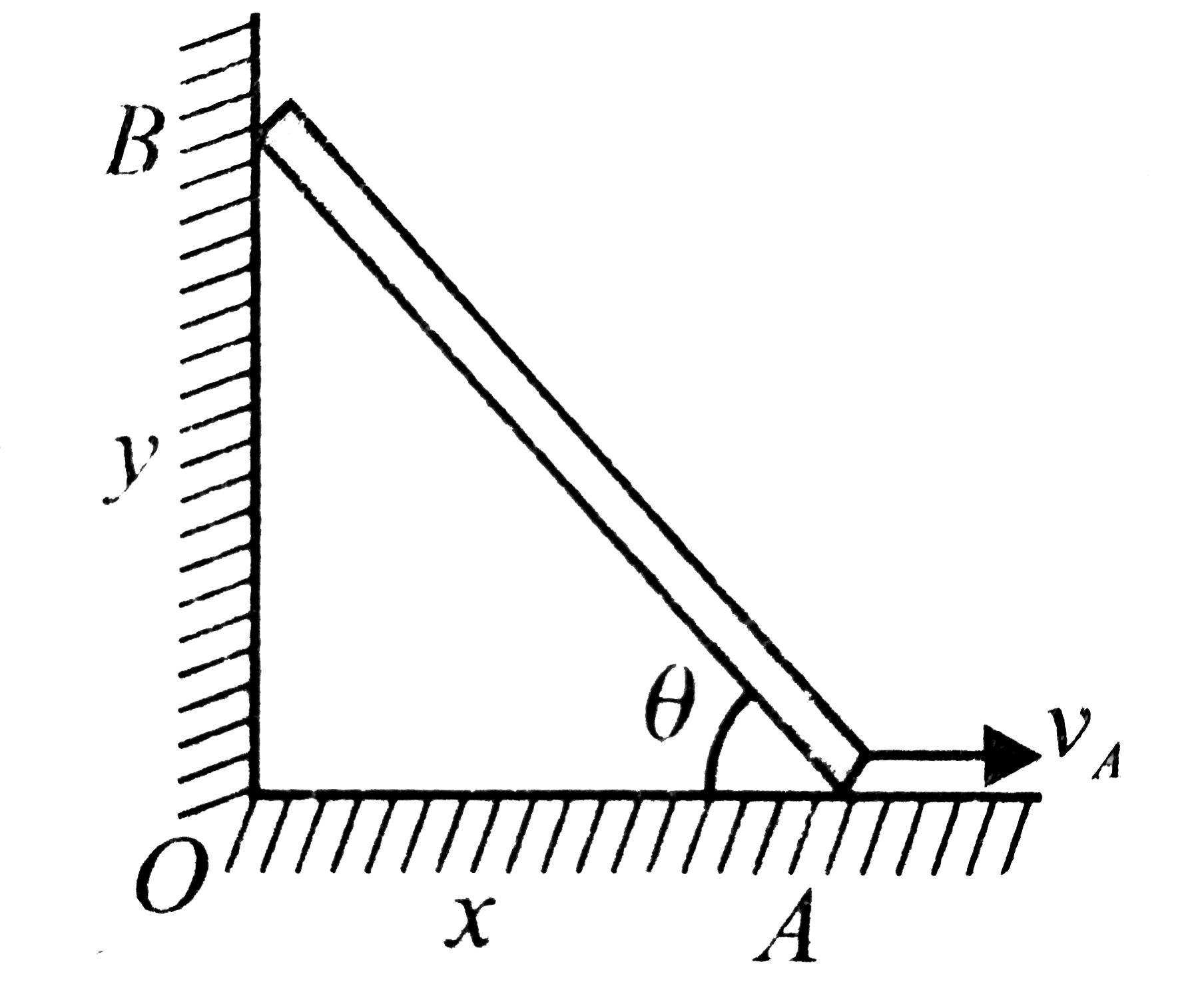
the velocity of the CM of the rod
View SolutionA rod of mass m and length l is sliding against a smooth vertical wall as shown. The speed of the bottom end of the rod at the instant shown is V0. The magnitude of angular momentum of the rod about ICR. (instantaneous axis of rotation) at the instant when θ=30∘ is
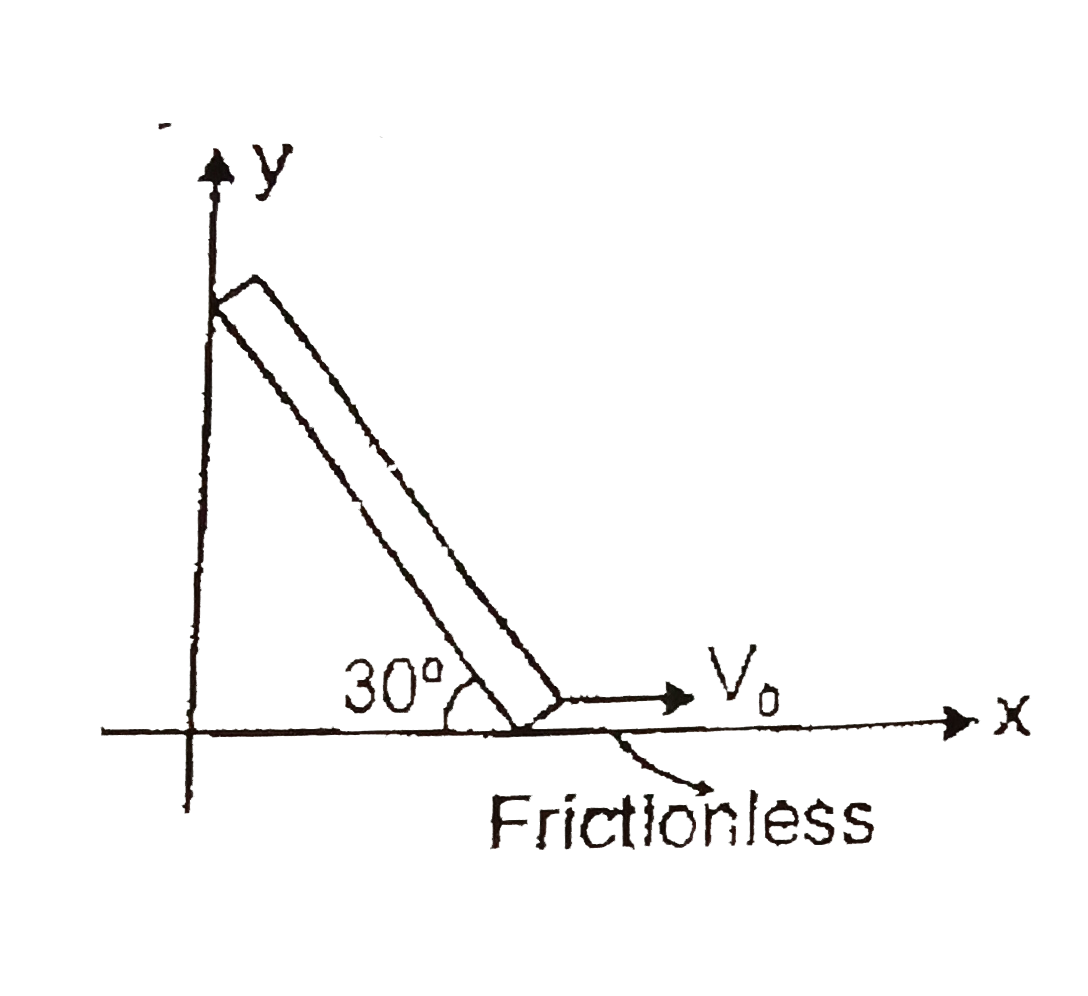
View Solution

