In the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
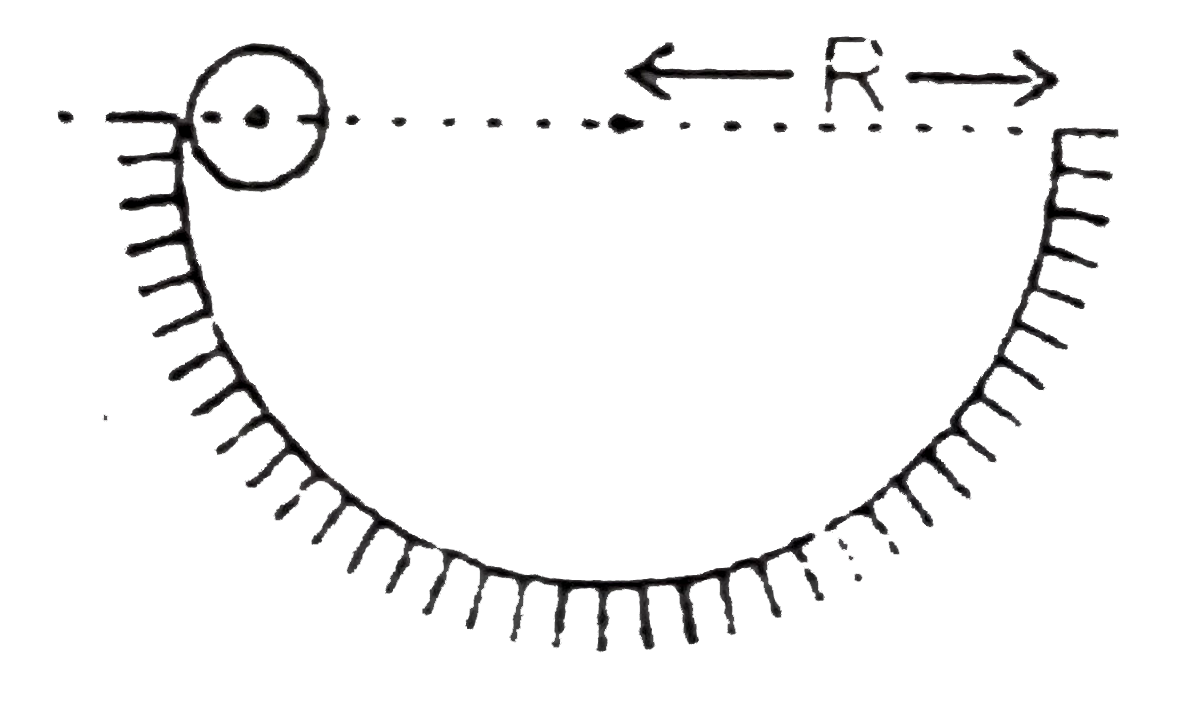
10mg7
17mg7
3mg7
zero
The correct Answer is:A
From conservation of energy, the kinetic energy of ball at lowest portion is (vc= speed of centre of ball)
12mv2c+12×25mv2c=mgR
or 710mv2c=mgR
Since net tangential force on sphere at lowest point is zero, net force on sphere at lowest position is
=mv2cR=107mg
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.62
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.63
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.60
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionA section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block is released from position A and leaves the track at B. The radius of curvature of itstrajectory when it just leaves the track at B is R. Find x.
'(##CEN_KSR_PHY_JEE_C07_027_Q16##)'
View Solution
Knowledge Check
In the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
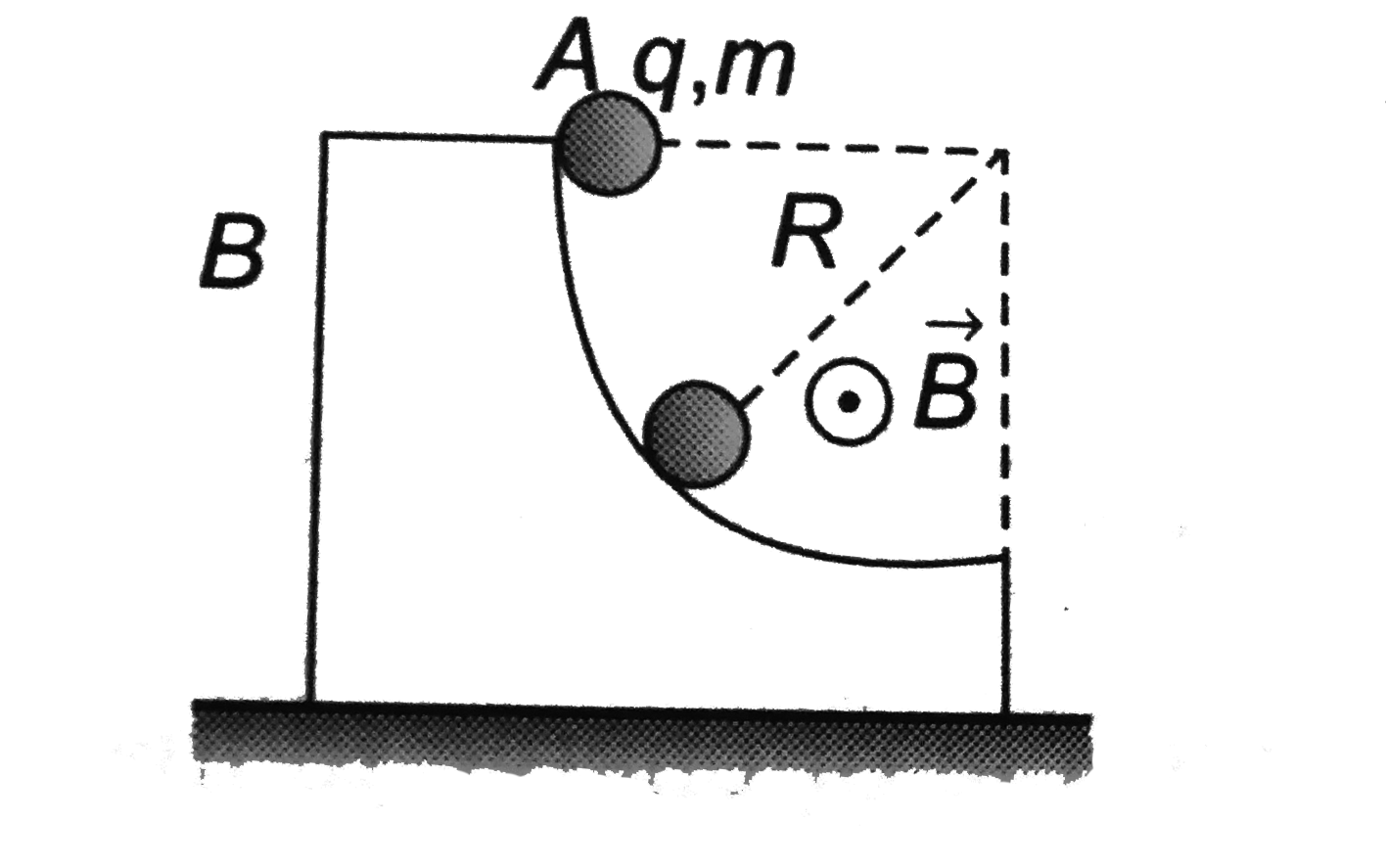 ANmax=2mg+qB√2gRBNmax=3mg+qB√2gRCNmax=3mg+2qB√2gRDNmax=3mg+qB√gR
ANmax=2mg+qB√2gRBNmax=3mg+qB√2gRCNmax=3mg+2qB√2gRDNmax=3mg+qB√gRA ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
.A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)A train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
A(a) zeroB(b) 2MvπC(c) MvRD(d) Mv
A train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA car is moving along a semicircular track ashsown in the figure in a duration of 2π second from P to Q. then choose the correct statement (s).
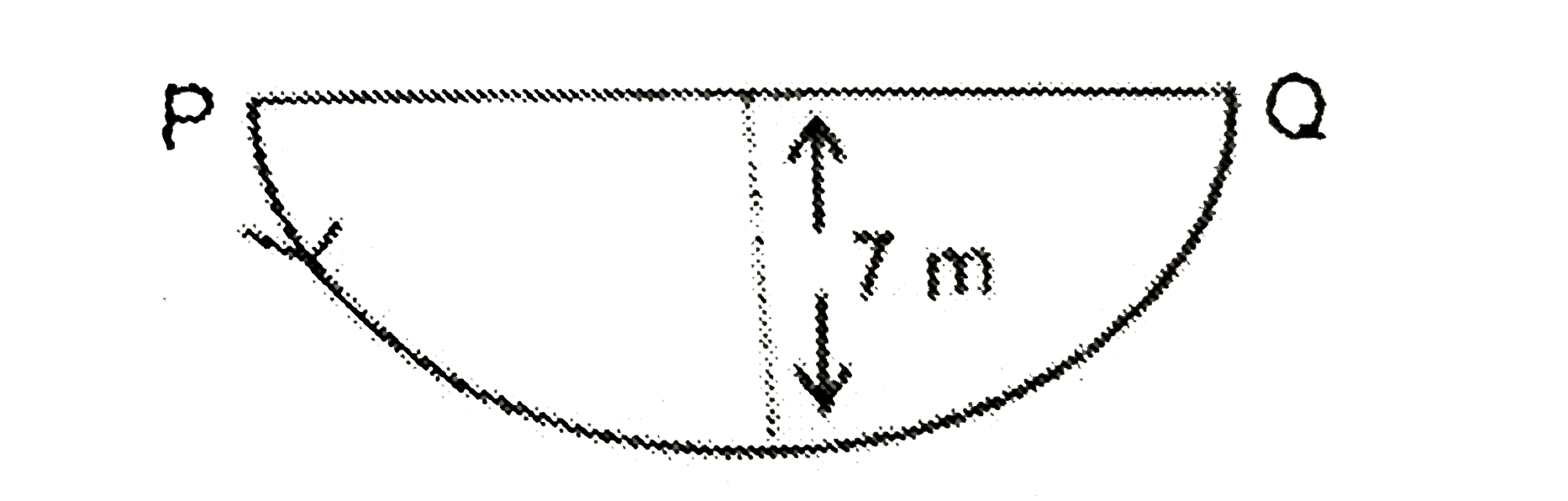
View SolutionA small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

Consider block to be at rest at top most point A of track. If the block is slowly pushed from rest at the highest A. When the spring reaches in horizontal state, then.
View SolutionA small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.
 If the block is released from rest when the spring is in horizontal state (see figure) then at that moment,
If the block is released from rest when the spring is in horizontal state (see figure) then at that moment,
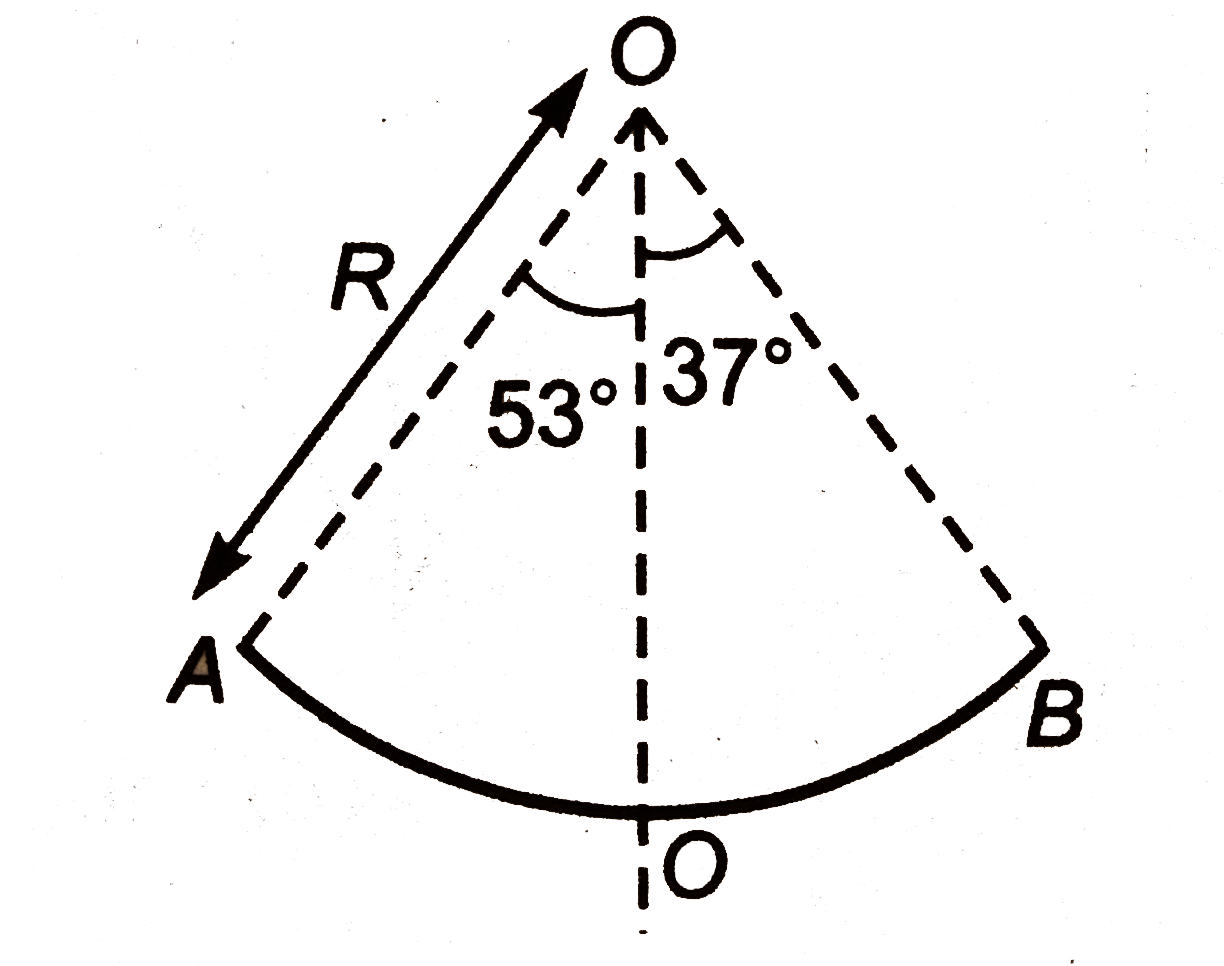
View SolutionA section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block id released from position A and leaves the track at B The radius of curvature of its trajectory just after it leaves the track B is ?
View Solution