A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

Consider block to be at rest at top most point A of track. If the block is slowly pushed from rest at the highest A. When the spring reaches in horizontal state, then.
Spring potential energy is (3kR24)(2−√3)
Spring potential energy is (kR28)(√3−1)2
Gravitational potential energy (taking U=0atθ=0) is (mgR2)
Gravitational potential energy (taking U=0atθ=0)is(3mgR8)
The correct Answer is:B
S.E.=12kR2(sinθ−12)2
12kR2(√3−12)2
=kR28(√3−1)2
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Multiple objective
Explore 131 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.
 If the block is released from rest when the spring is in horizontal state (see figure) then at that moment, Atangential acceleration is g √32−kR4m(√3−1)Bradial acceleration is g2+kR√34m(√3−1)Ctangential acceleration is g2−kR√34m(√3−1)Dradial acceleration is g√32−kR4m(√3−1)
If the block is released from rest when the spring is in horizontal state (see figure) then at that moment, Atangential acceleration is g √32−kR4m(√3−1)Bradial acceleration is g2+kR√34m(√3−1)Ctangential acceleration is g2−kR√34m(√3−1)Dradial acceleration is g√32−kR4m(√3−1)A small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

If the complete stup is in a gravity free space, then the minimum speed (v_(0)) required at the highest point A to just reach the lowest point isA2R√kmB3R2√kmCR√kmDMotion not possible in gravity free space.A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
View SolutionA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown

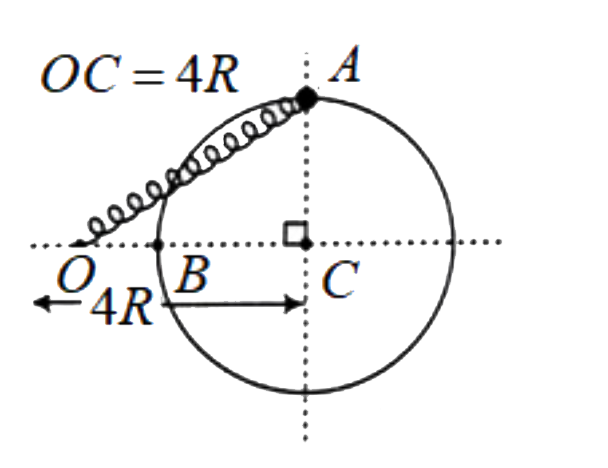
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionA bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View Solution

