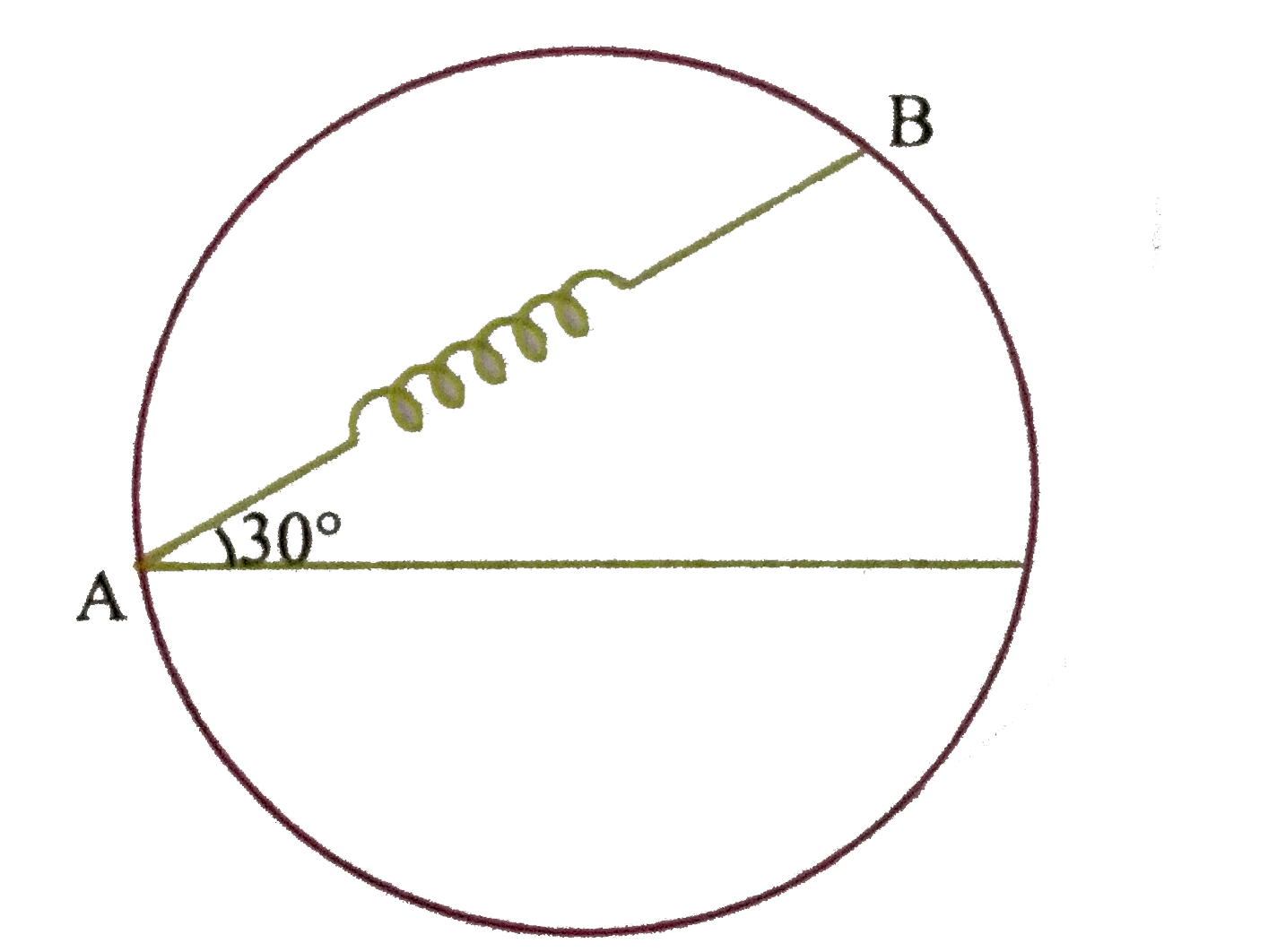
A Bead of mass is attached to one end of a spring of natural length and spring cosntant . The other end of the spring is fixed at point on a smooth vertical ring of radius as shown
The correct Answer is:D
Extension in the spring is
Spring force:
From the fig, we have
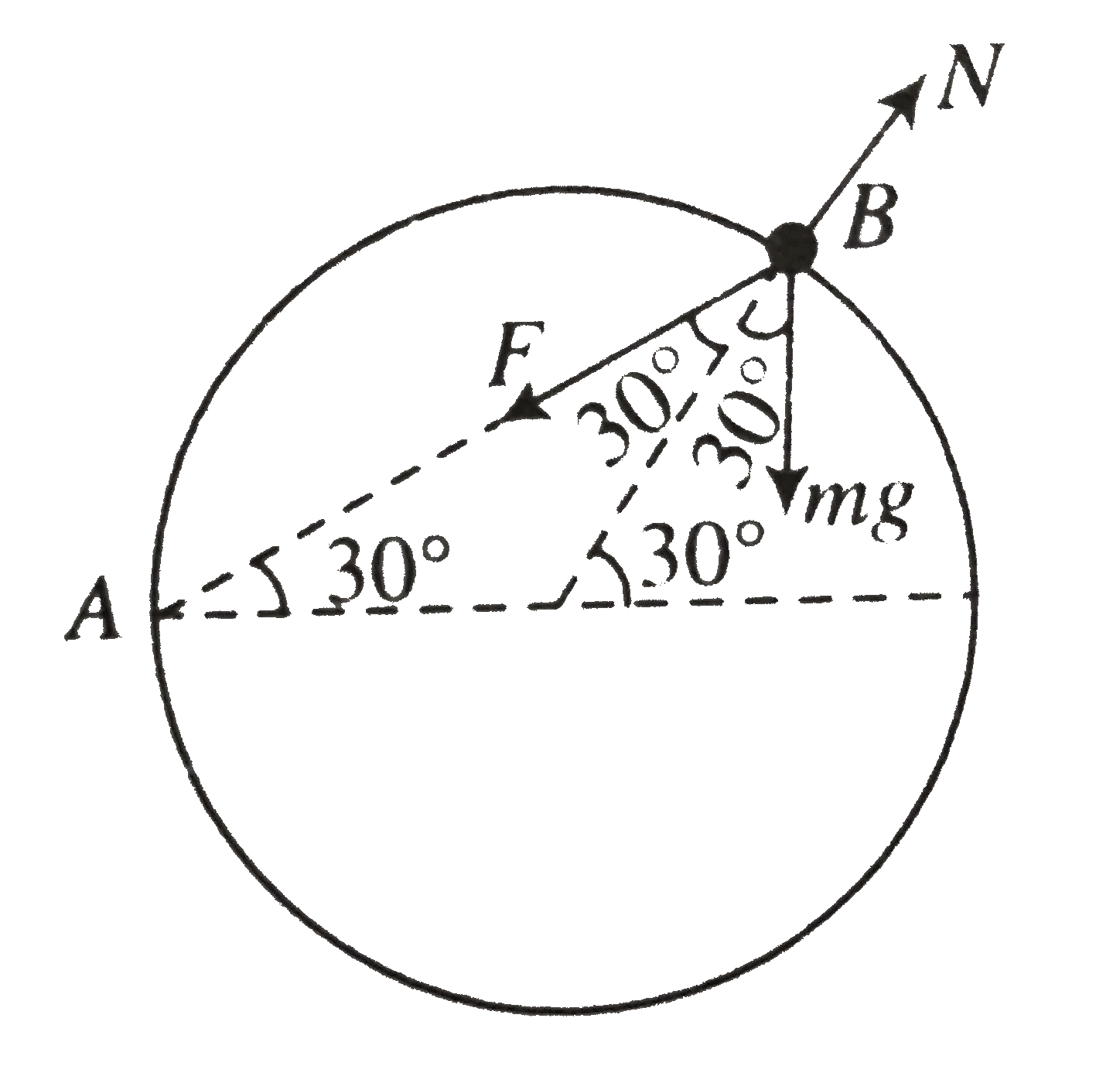
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
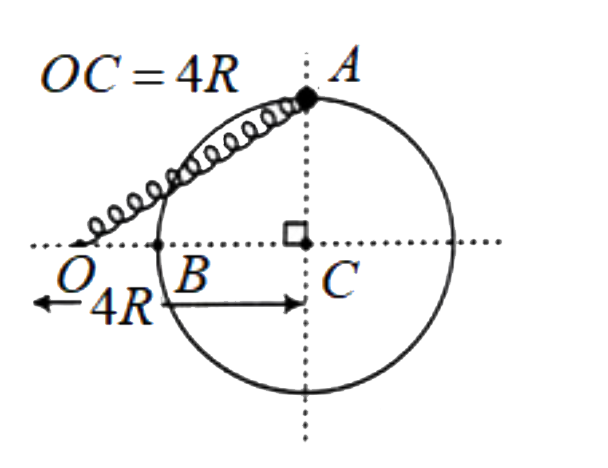
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View Solution
Knowledge Check
A Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 Amg/2B√3mgC3√3mgD3√3mg2
Amg/2B√3mgC3√3mgD3√3mg2A bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is
 A√3mgB3√3mgCmg2D3√3mg2
A√3mgB3√3mgCmg2D3√3mg2A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
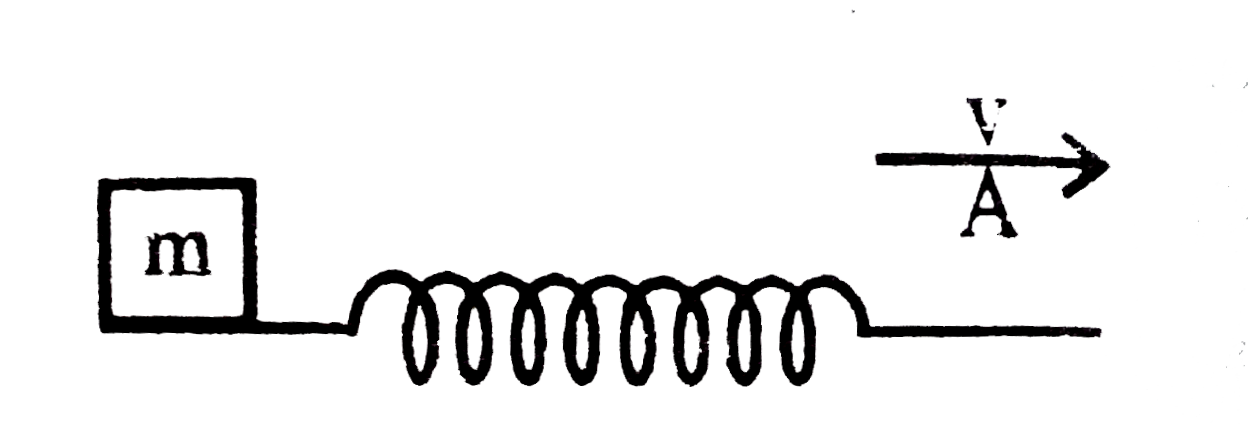 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

Consider block to be at rest at top most point A of track. If the block is slowly pushed from rest at the highest A. When the spring reaches in horizontal state, then.
View SolutionA small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.
 If the block is released from rest when the spring is in horizontal state (see figure) then at that moment,
If the block is released from rest when the spring is in horizontal state (see figure) then at that moment,
View SolutionA small block of mass m, can move without friction on the outside of a fixed vertical circular track of radiusR. The block is attached to a spring of natural length R/2 and spring constant K. The other end of spring is connected to a point at height R/2 directly above the centre of track.

If the complete stup is in a gravity free space, then the minimum speed (v_(0)) required at the highest point A to just reach the lowest point is
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View Solution
