A particle of mass $1.5$ kg moves along x-axis in a conservative force field. Its potential energy is given by $V (x) = 2 x^{3} - 9 x^{2} + 12 x,$ where all quantities are written in SI units. The plot of this potential energy is given below.
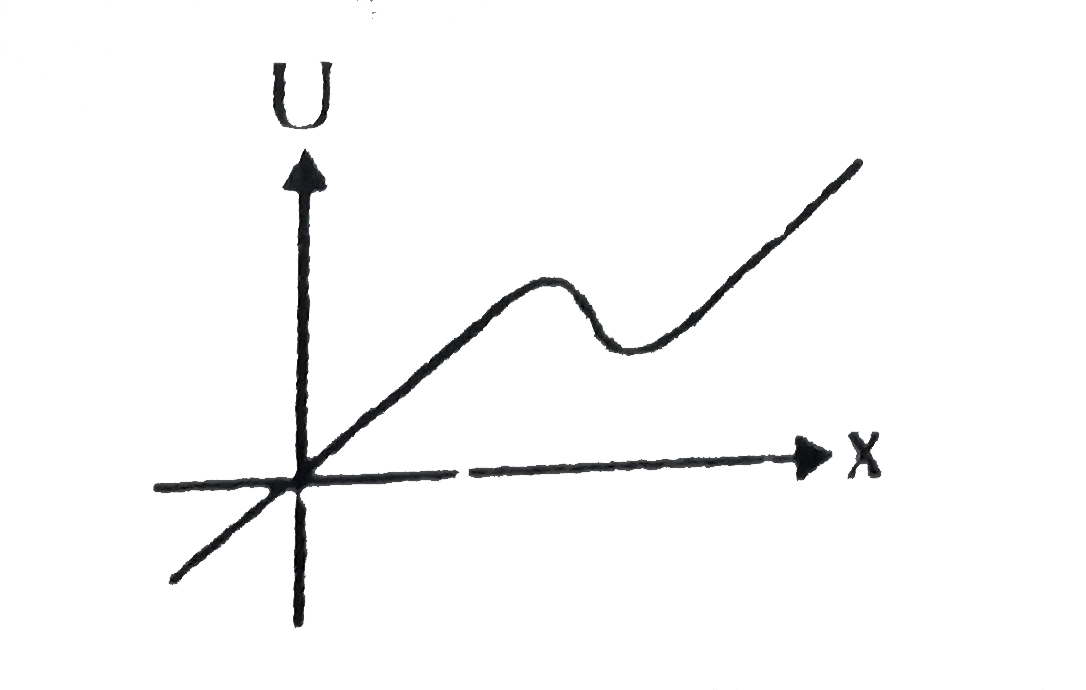It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the range of total mechanical energy of the particle for which its motion can be oscillatory about a point

$E < 5 J$

$E < 8 J$

$E < 12 J$

$E < 9 J$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A particle of mass $1.5$ kg moves along x-axis in a conservative force field. Its potential energy is given by $V (x) = 2 x^{3} - 9 x^{2} + 12 x,$ where all quantities are written in SI units. The plot of this potential energy is given below.
It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the value of $x_{0}$ ?
A2m
B3m
C1m
D $1.5$ m
A particle of mass $1.5$ kg moves along x-axis in a conservative force field. Its potential energy is given by $V (x) = 2 x^{3} - 9 x^{2} + 12 x,$ where all quantities are written in SI units. The plot of this potential energy is given below.
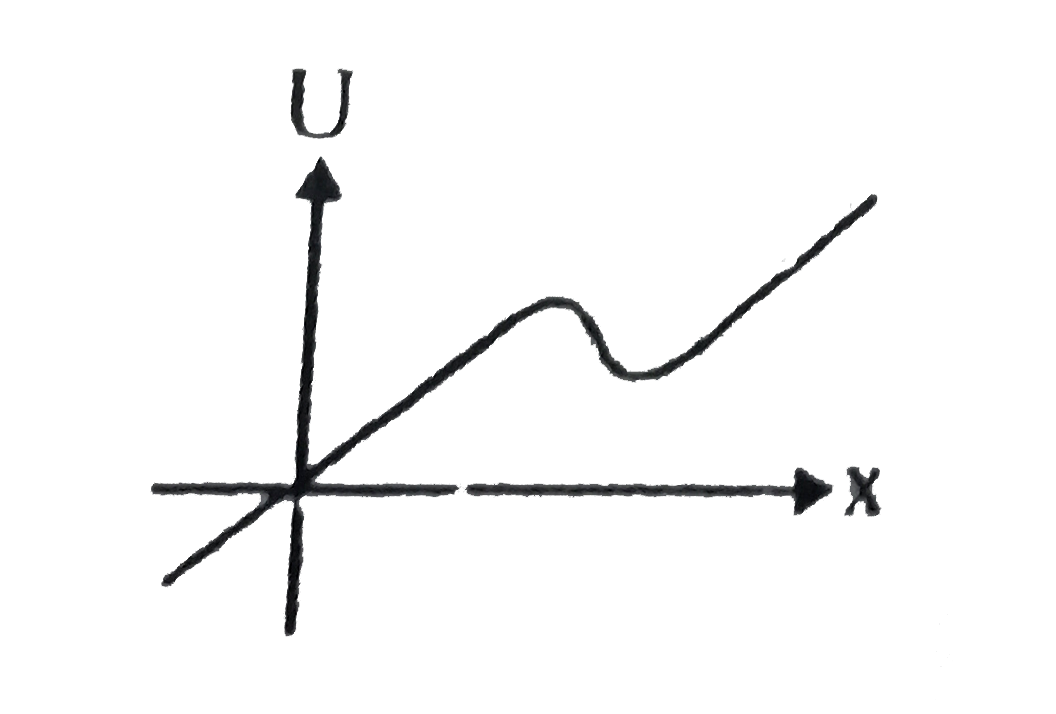It is seen that the particle can be in stable equilibrium at a point on x-axis, x_(0). When it is displaced slightly from this equilibrium position, It executes SHM with time period T. What is the time period of SHM mentioned in the paragraph?
A $π sec$
B $2 π sec$
C $\frac{π}{2} sec$
D $\frac{π}{4} sec$
A particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as $U (x) = α x^{4}$ , where $α$ is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
A $\pm \frac{A}{2}$
B $\pm \frac{A}{\sqrt{2}}$
C $\pm \frac{A}{3}$
D $\pm \frac{A}{\sqrt{3}}$