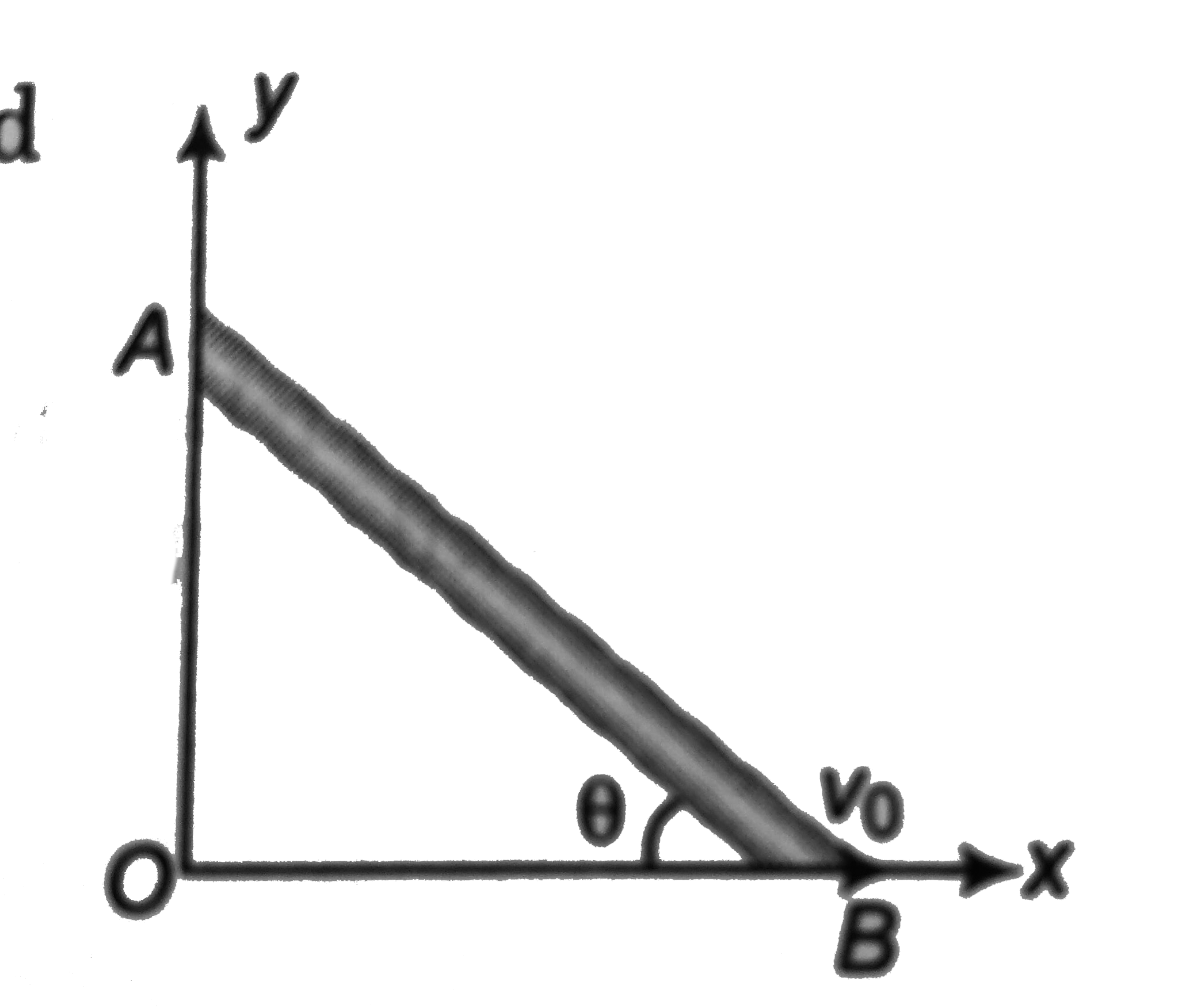
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
(a)At θ=37∘ velocity of end A is 43v0 downwards
(b)At θ=37∘ angular velocity of rod is 5v03l
(c)Angular velocity of rod is constant
(d)velocity of end A is constant.

Velocity component along AB=0
∴v0cosθ=vsinθ
or v=v0cotθ=f1(θ)
at θ=37∘,v=43v0
ω=relative velocity ⊥to ABl
=v0sinθ+vcosθl=f2(θ)
=(v0)(3/5)+(4/3v0)(4/5)l=5v03l
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
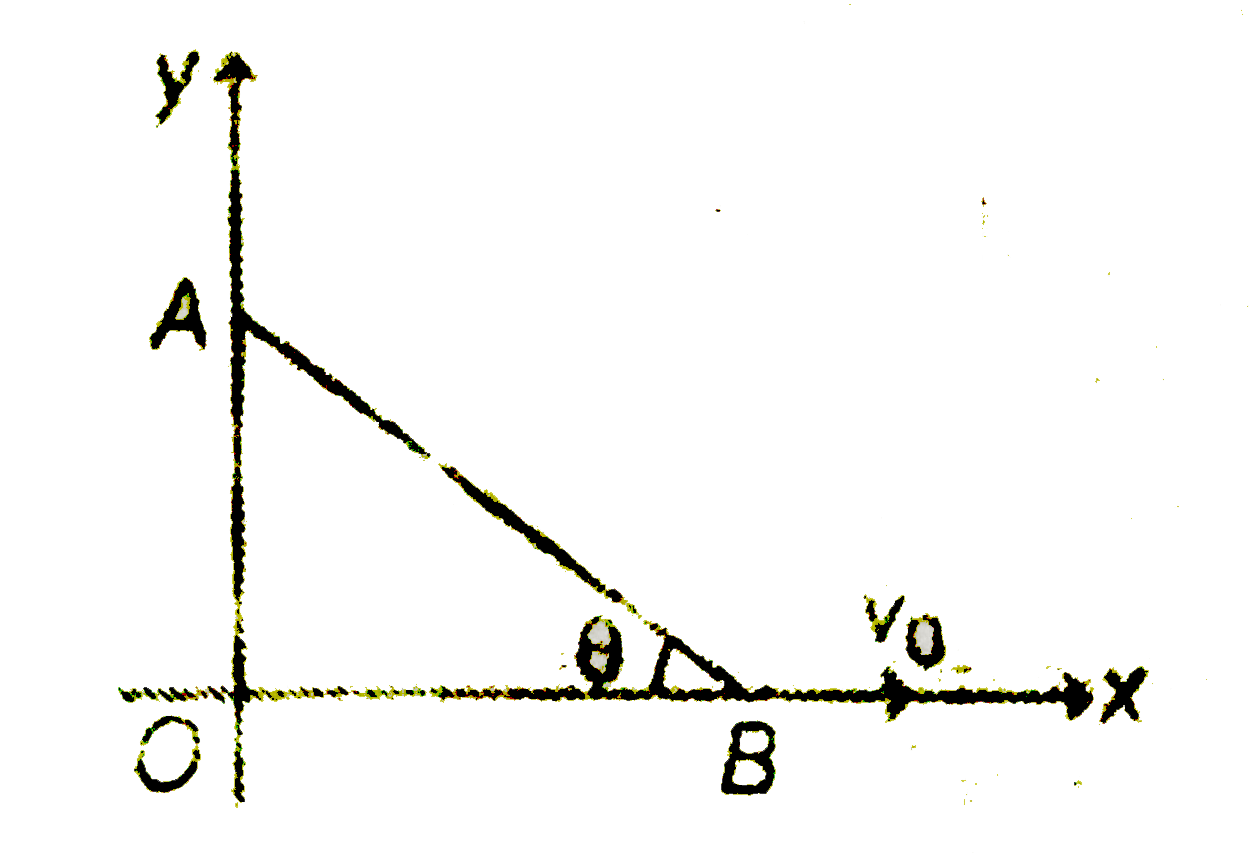
(A)velocity of end A is 43v0 downwards
(B)angular velocity of rod is 53v0l
(C)angular velocity of rod is constant
(D)velocity of end A is constant
View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .

View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)

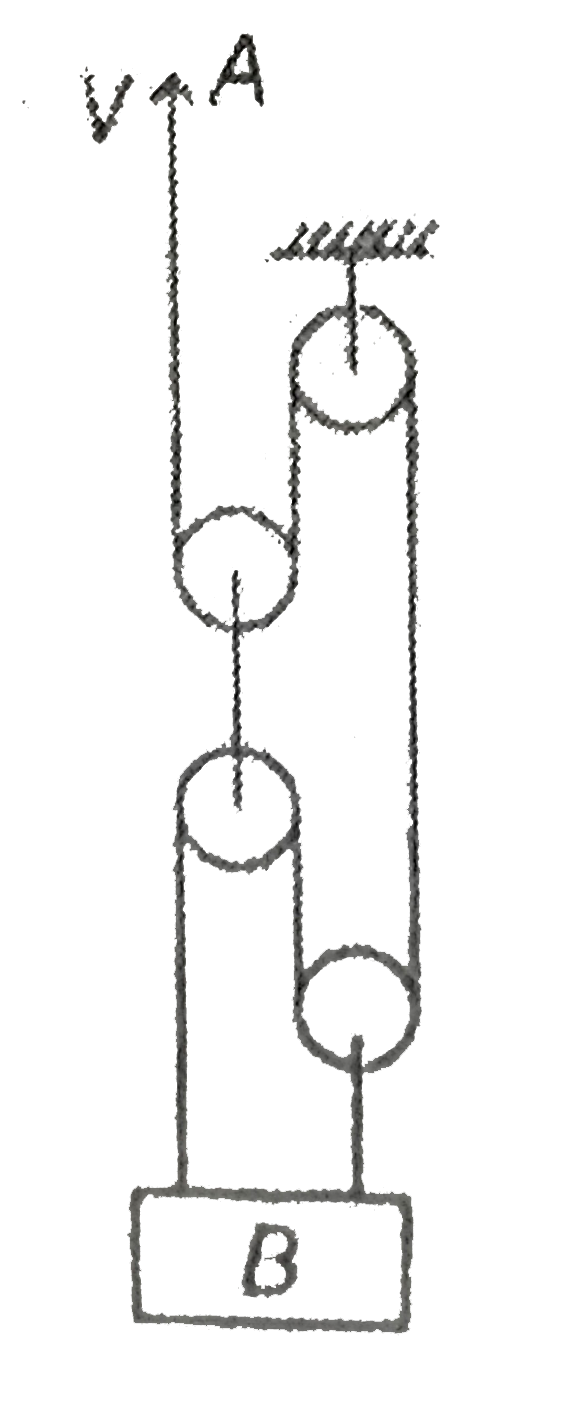
View SolutionIn the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
View SolutionFigure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

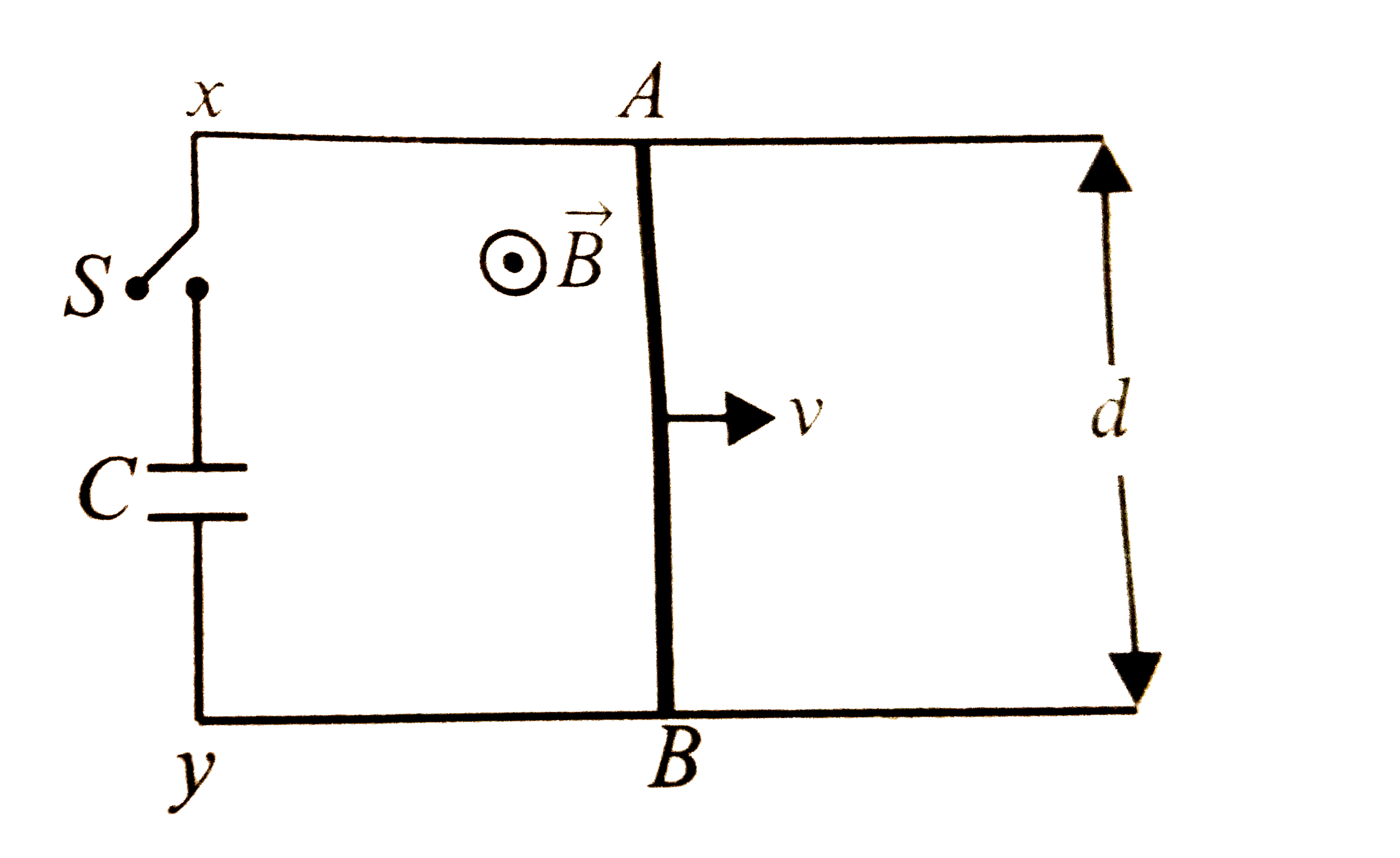
View SolutionA sliding rod AB of resistance R is shown in the figure. Here magnetic field B is constant and is out of the paper. Parallel wires have no resistance and the rod is moving with constant velocity v. The current in the sliding rod AB when switch S is closed at time t=0 is
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA conducting rod of length l falls verticaly under gravity in a region of uniform magnetic field B. The field vectors are inclined at an angle θ with the horizontal as shown in figure. If the instantaneous velocity of the rod is v, the induced emf in the rod ab is
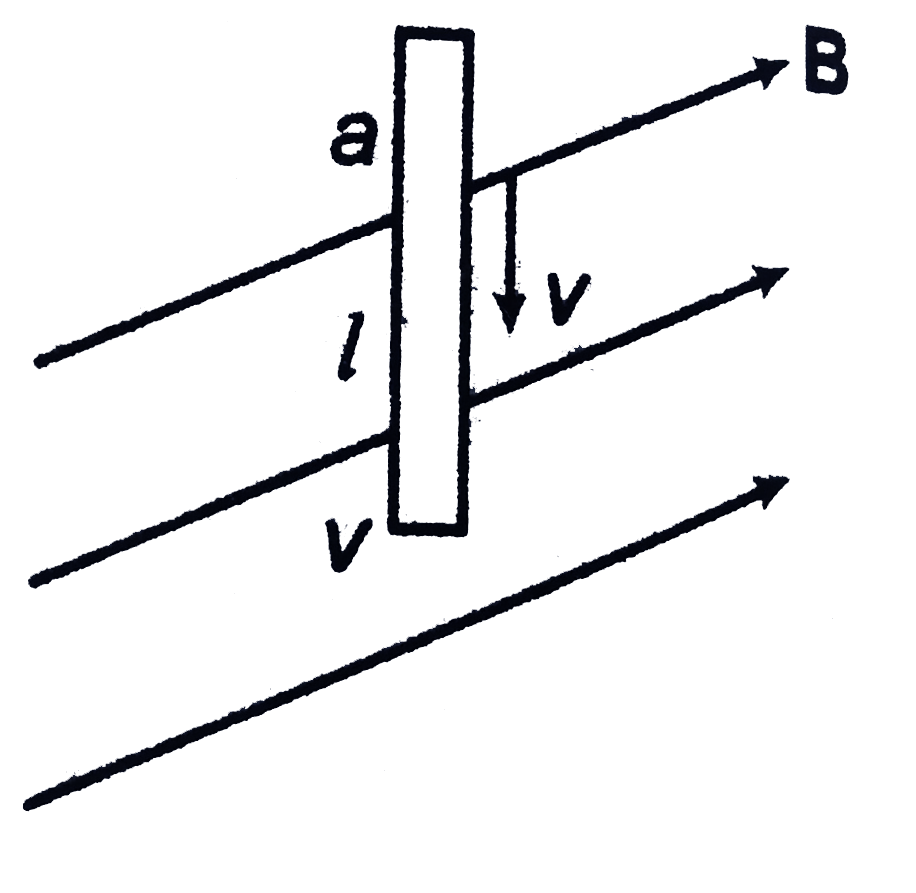
View SolutionA disk is fixed at its centre O and rotating with constant angular velocity ω. There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30∘ with the vertical the ring is found to have a velocity v in the upward direction. Find ω of the disk. Given that the point A is R/2 distance above point O and length of the rod Ab is l
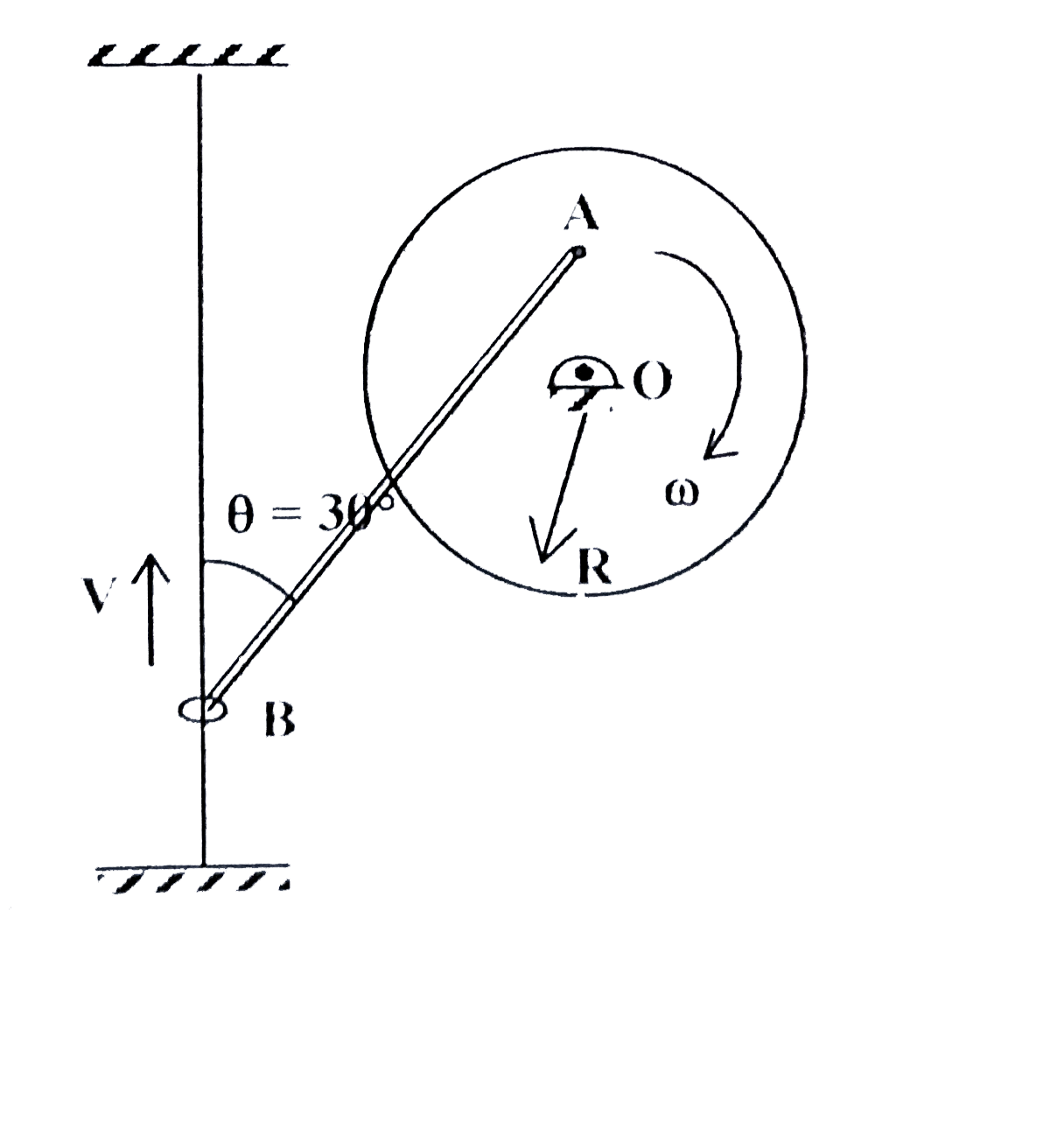
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View Solution
