A non-uniform ball of radius R and radius of gyration about geometric centre =R/2 is kept on a frictionless surface. The geometric centre coincides with the centre of mass. The ball is struck horizontally with a sharp impulse =J the point of application of the impulse is at a height h above the surface. then.
(a)The ball will slip on surface for all cases
(b)the ball will roll purely if h=5R/4
(c)the ball will roll purely if h=3R/2
(d)there will be no rotation if h=R
To solve the problem step by step, we will analyze the situation described and apply the principles of linear and angular momentum.
Step 1: Understand the System
We have a non-uniform ball of radius R with a radius of gyration k=R2. The ball is on a frictionless surface, and the center of mass coincides with the geometric center. An impulse J is applied horizontally at a height h above the surface.
Step 2: Define the Parameters
- Radius of the ball: R
- Radius of gyration: k=R2
- Distance from the center of the ball to the point of application of impulse:
r=h−R
Step 3: Calculate Linear Impulse
The linear impulse J leads to a change in linear momentum. If the initial velocity vi=0, then:
J=m⋅vf⇒vf=Jm
Step 4: Relate Linear and Angular Motion
The relationship between linear velocity v and angular velocity ω for rolling motion is given by:
v=R⋅ω
Step 5: Calculate Angular Impulse
The angular impulse K due to the applied impulse is given by:
K=J⋅r
Where r is the distance from the center of mass to the point of application of the impulse.
Step 6: Change in Angular Momentum
The change in angular momentum is given by:
K=I⋅ω
Where I is the moment of inertia of the ball. The moment of inertia I can be calculated using the radius of gyration:
I=m⋅k2=m⋅(R2)2=mR24
Step 7: Set Up the Equation
Equating the angular impulse to the change in angular momentum:
J⋅(h−R)=mR24⋅ω
Substituting ω=vfR=JmR:
J⋅(h−R)=mR24⋅JmR
This simplifies to:
J⋅(h−R)=JR4
Step 8: Solve for h
Dividing both sides by J (assuming J≠0):
h−R=R4
Thus,
h=R+R4=5R4
Conclusion
The height h at which the impulse must be applied for the ball to roll without slipping is:
h=5R4
We have a non-uniform ball of radius R with a radius of gyration k=R2. The ball is on a frictionless surface, and the center of mass coincides with the geometric center. An impulse J is applied horizontally at a height h above the surface.
- Radius of the ball: R
- Radius of gyration: k=R2
- Distance from the center of the ball to the point of application of impulse:
r=h−R
The linear impulse J leads to a change in linear momentum. If the initial velocity vi=0, then:
J=m⋅vf⇒vf=Jm
The relationship between linear velocity v and angular velocity ω for rolling motion is given by:
v=R⋅ω
The angular impulse K due to the applied impulse is given by:
K=J⋅r
Where r is the distance from the center of mass to the point of application of the impulse.
The change in angular momentum is given by:
K=I⋅ω
Where I is the moment of inertia of the ball. The moment of inertia I can be calculated using the radius of gyration:
I=m⋅k2=m⋅(R2)2=mR24
Equating the angular impulse to the change in angular momentum:
J⋅(h−R)=mR24⋅ω
Substituting ω=vfR=JmR:
J⋅(h−R)=mR24⋅JmR
This simplifies to:
J⋅(h−R)=JR4
Dividing both sides by J (assuming J≠0):
h−R=R4
Thus,
h=R+R4=5R4
The height h at which the impulse must be applied for the ball to roll without slipping is:
h=5R4
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Subjective
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3R
Determine the centre of mass of a uniform hemisphere of radius R.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA solid sphere rests on a horizontal surface. A horizontal impulse is applied at height h from centre. The sphere starts rolling just after the application of impulse. The ratio h/R will be
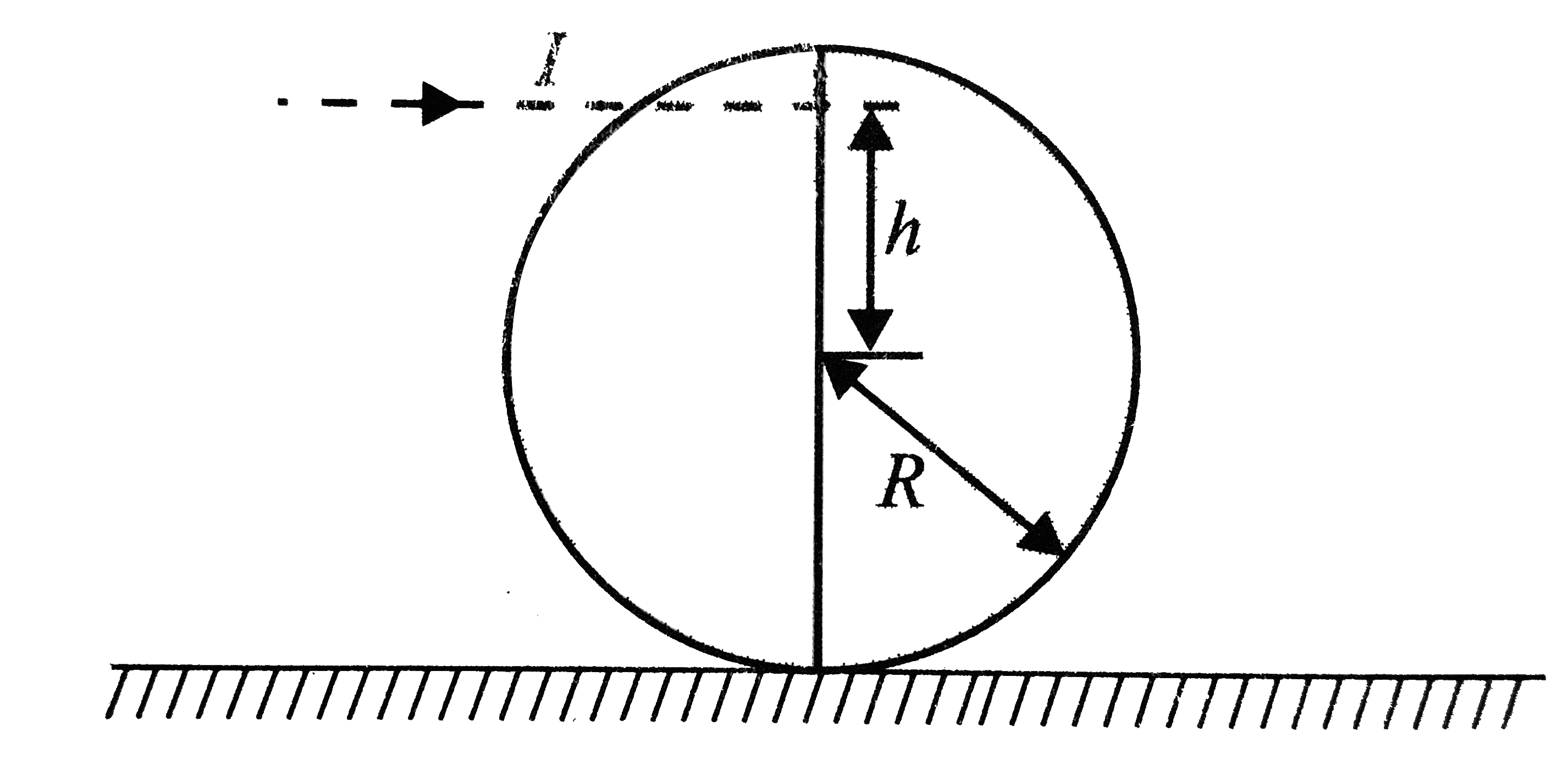
View SolutionA solid spherical ball kept on a horizontal surface is struck by a que at height h above the central line

View SolutionA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA ball kept in a close box moves in the box making collisions with the walls. The box is kept on a smooth surface. The velocity of the centre of mass
View Solution