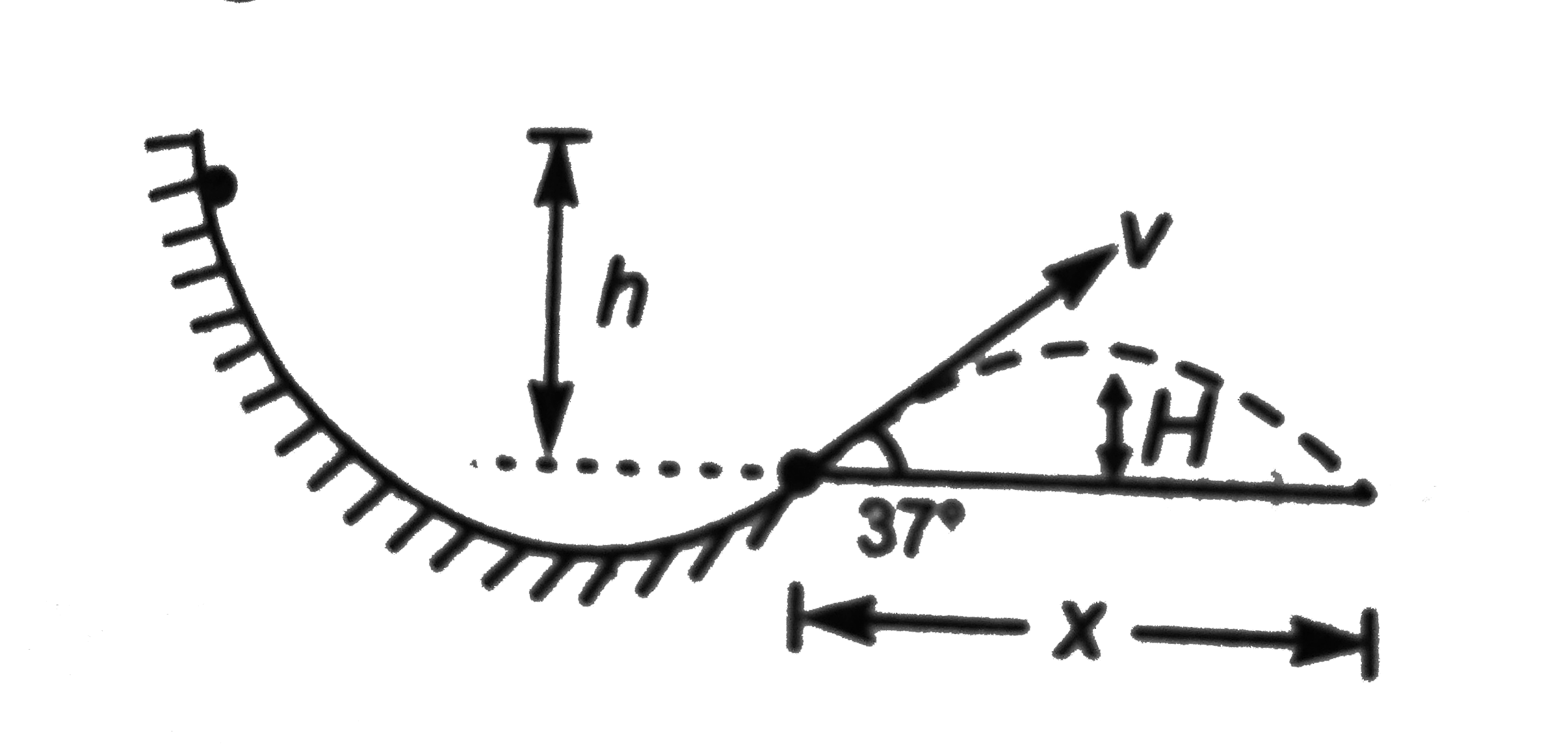
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball is
144125h
4825h
4835h
247h
R=x=2u2sin37∘cos37∘g
=(2)(6gh/5)(3/5)(4/5)g
=144125h
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Subjective
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
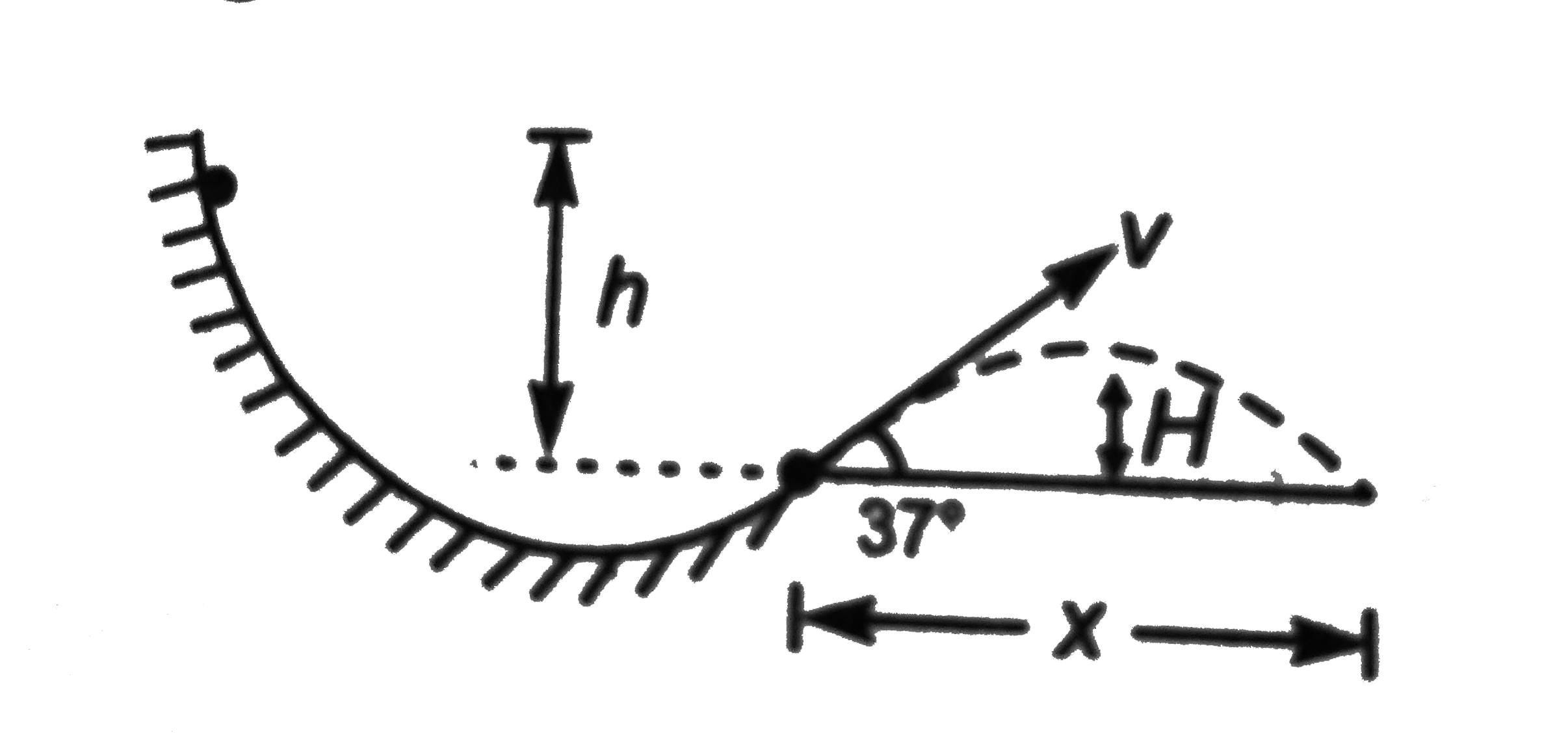
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
View Solution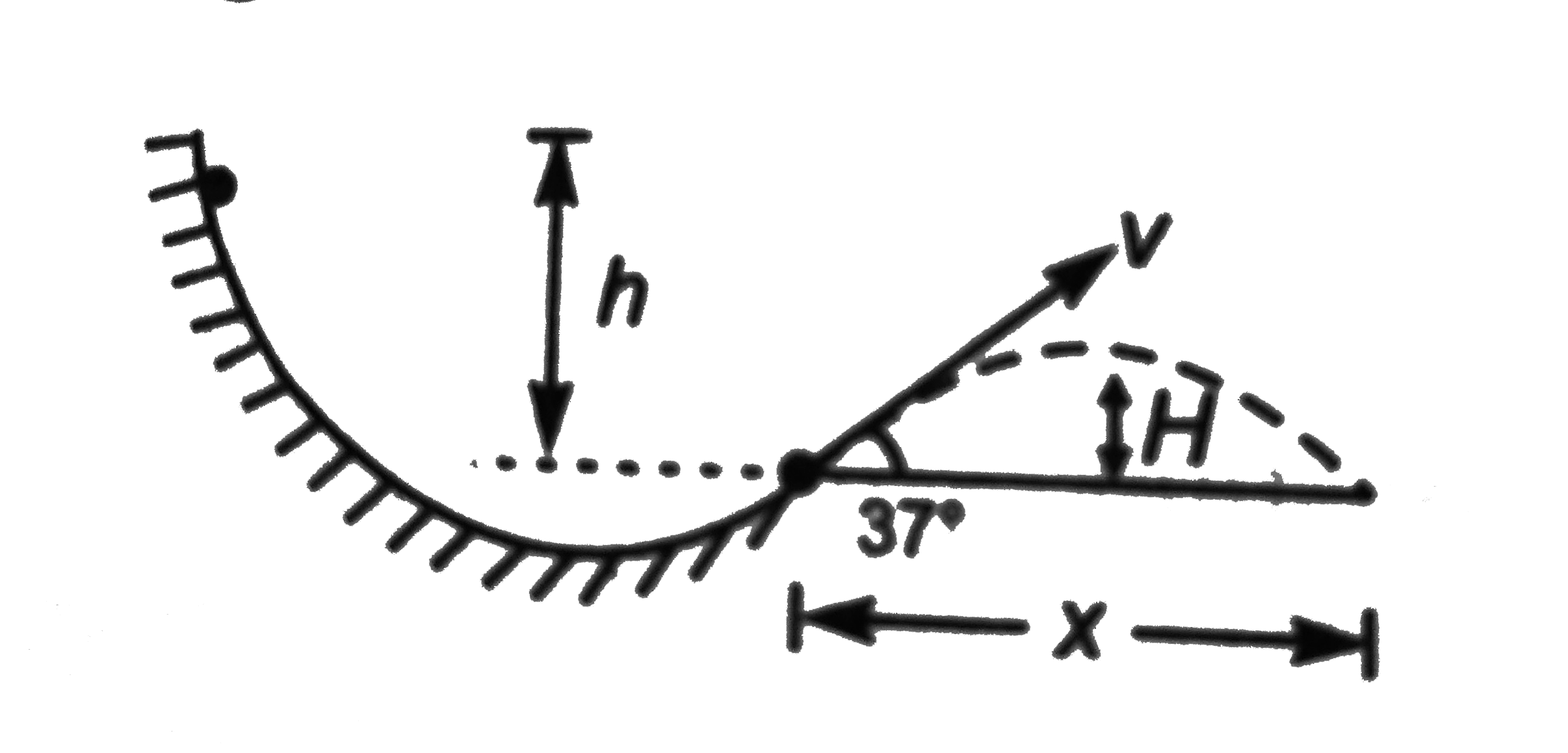
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v is
View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of 9ms−1 with respect to the ground. The rotational speed of the platform in rads−1 after the balls leace the platform is
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
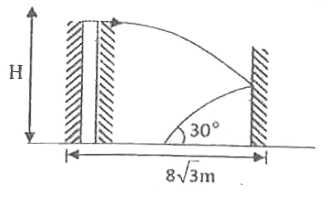
View SolutionA ball is thrown horizontally from the top of a lower of unkown height .Ball strikes a vertical wall whose plane is normal to the plane of month of ball Collison is elastic and ball falls on ground exactly at the midpoints between the lower and the wall ball strikes the grouind at an angle of the 30∘ with horizontal .Find the hieght of the tower (in meter)
View SolutionA balloon starts from rest from the ground and moves with uniform acceleration g/8. When it reaches a height h a ball is dropped from it. Find the time taken by the ball to reach the ground.

View SolutionA smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane.
a. If e=0, find the speed of the ball just after leaving the inclined plane 1.
b. If the particle mioves horizontally just after the collision find e.

View SolutionStarting from rest, A lift moves up with an acceleration of 2ms−2. In this lift , a ball is dropped from a height of 1.5m (with respect to floor of lift). The time taken by the ball to reach the floor of the lift is (g=10ms−2)
View SolutionA ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
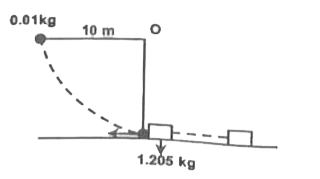
View SolutionA ball of mass 0.01 kg is suspended from a fixed point O by means of a light and inextensible string of length 10m. The ball is first taken aside such that string becomes horizontal and then released from reast. At the lowermost point of its path, it hits a stationary small block of mass 1.205kg lying on a rough horizontal surface. After striking the block, the ball rebounds and comes to rest when the string makes an angle of 30∘) with the horizontal . Due to the impact the block moves through a distance of 0.5m on the horizontal surface. Find the coefficient of friction between the block and the surface.
View Solution

