A ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
The correct Answer is:8 m
To solve the problem step by step, we will break it down into manageable parts.
Step 1: Understand the Problem
We have a ball thrown from the top of a tower with an initial velocity of 10 m/s at an angle of 37 degrees above the horizontal. It hits the ground at a distance of 16 m from the base of the tower. We need to find the height of the tower.
Step 2: Resolve the Initial Velocity
The initial velocity can be resolved into horizontal and vertical components using trigonometric functions:
- ux=ucos(37∘)
- uy=usin(37∘)
Given u=10m/s:
- ux=10cos(37∘)
- uy=10sin(37∘)
Using the values of cosine and sine:
- cos(37∘)=45
- sin(37∘)=35
Calculating the components:
- ux=10×45=8m/s
- uy=10×35=6m/s
Step 3: Calculate Time of Flight
Using the horizontal motion to find the time of flight:
- The horizontal distance covered is x=16m.
- The formula for horizontal motion is:
x=ux⋅t
Substituting the values:
16=8⋅t
Solving for t:
t=168=2s
Step 4: Analyze Vertical Motion
Now, we will analyze the vertical motion to find the height of the tower. The vertical displacement h can be calculated using the kinematic equation:
s=ut+12at2
Here, s=−h (downward displacement), u=uy=6m/s, a=−g=−10m/s2, and t=2s.
Substituting the values into the equation:
−h=6⋅2+12⋅(−10)⋅(22)
Calculating:
−h=12−12⋅10⋅4
−h=12−20
−h=−8
Thus, the height of the tower h is:
h=8m
Final Answer
The height of the tower is 8 meters.
---
We have a ball thrown from the top of a tower with an initial velocity of 10 m/s at an angle of 37 degrees above the horizontal. It hits the ground at a distance of 16 m from the base of the tower. We need to find the height of the tower.
The initial velocity can be resolved into horizontal and vertical components using trigonometric functions:
- ux=ucos(37∘)
- uy=usin(37∘)
- ux=10cos(37∘)
- uy=10sin(37∘)
- cos(37∘)=45
- sin(37∘)=35
- ux=10×45=8m/s
- uy=10×35=6m/s
Using the horizontal motion to find the time of flight:
- The horizontal distance covered is x=16m.
- The formula for horizontal motion is:
x=ux⋅t
Substituting the values:
16=8⋅t
Solving for t:
t=168=2s
Now, we will analyze the vertical motion to find the height of the tower. The vertical displacement h can be calculated using the kinematic equation:
s=ut+12at2
Here, s=−h (downward displacement), u=uy=6m/s, a=−g=−10m/s2, and t=2s.
−h=6⋅2+12⋅(−10)⋅(22)
Calculating:
−h=12−12⋅10⋅4
−h=12−20
−h=−8
Thus, the height of the tower h is:
h=8m
The height of the tower is 8 meters.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
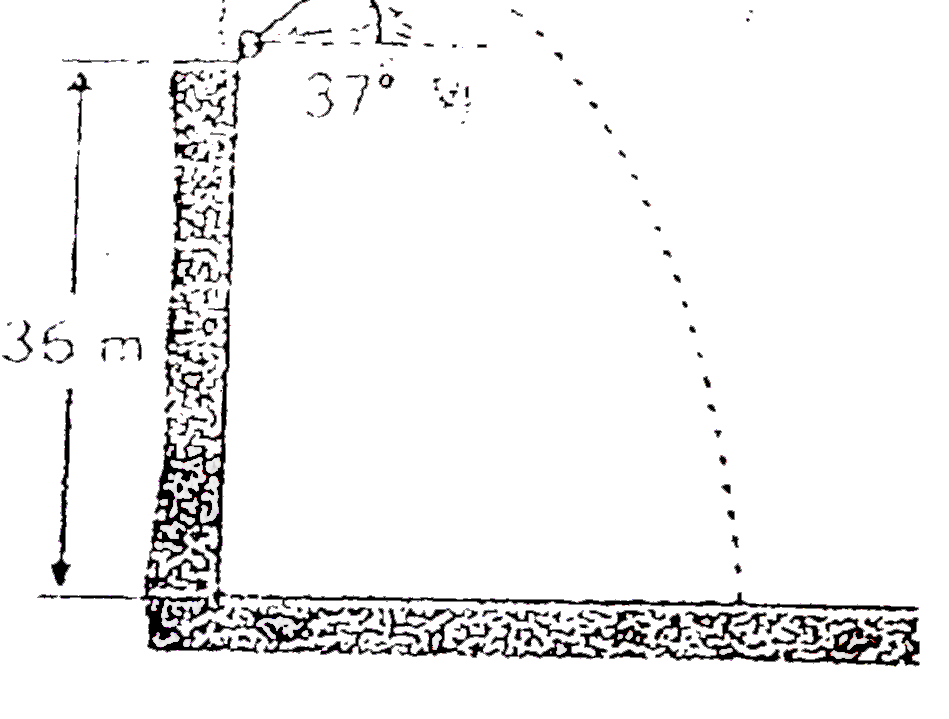 :
:
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 ms−1 . The ball reaches the ground after 5s. Calculate the height of the tower .
View Solution
Knowledge Check
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA ball is thrown upwards from the top of a tower 40m high with a velocity of 10m/s. Find the time when it strikes the ground. Take g=10m/s2.
View SolutionA pebbel is thrown horizantally from the top of a 20 m high tower with an initial velocity of 10m/s.The air drag is negligible . The speed of the peble when it is at the same distance from top as well as base of the tower (g=10m/s2)
View SolutionA ball is throw from the top of a tower of 61 m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizon. What is the distance from the foot of the tower to the point where the ball hits the ground ?
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6m s−1. The ball reaches the ground after 5 s. Calculate the height of the tower . Take g=9.8ms−2 ?
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View Solution
