A block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
Mg/k
2Mg/k
4Mg/k
Mg/2k
The correct Answer is:B
To solve the problem of finding the maximum extension of a spring when a mass is attached and released from rest, we can follow these steps:
1. Understanding the System:
- We have a spring with spring constant k that is hung from the ceiling, and a mass m is attached to the lower end of the spring. Initially, the spring is unstretched.
2. Initial Conditions:
- When the mass is released from rest, the spring is at its natural length, meaning the potential energy of the mass and the spring is zero.
3. Maximum Extension:
- Let x be the maximum extension of the spring from its natural length. At this point, the mass has fallen a distance x.
4. Energy Conservation:
- Since there are no external forces acting on the system between the initial and maximum extension points, we can apply the principle of conservation of energy.
- The potential energy lost by the mass when it falls a distance x is given by:
Potential Energy of mass=−mgx
- The potential energy stored in the spring when it is stretched by x is:
Potential Energy of spring=12kx2
5. Setting Up the Energy Conservation Equation:
- The loss in potential energy of the mass equals the gain in potential energy of the spring:
mgx=12kx2
6. Rearranging the Equation:
- Rearranging gives:
kx2−2mgx=0
- Factoring out x:
x(kx−2mg)=0
7. Solving for x:
- This gives us two solutions: x=0 (the trivial solution) or:
kx=2mg⟹x=2mgk
8. Conclusion:
- The maximum extension x of the spring when the mass is released from rest is:
x=2mgk
Final Answer:
The maximum extension produced in the length of the spring will be 2mgk.
---
- We have a spring with spring constant k that is hung from the ceiling, and a mass m is attached to the lower end of the spring. Initially, the spring is unstretched.
- When the mass is released from rest, the spring is at its natural length, meaning the potential energy of the mass and the spring is zero.
- Let x be the maximum extension of the spring from its natural length. At this point, the mass has fallen a distance x.
- Since there are no external forces acting on the system between the initial and maximum extension points, we can apply the principle of conservation of energy.
- The potential energy lost by the mass when it falls a distance x is given by:
Potential Energy of mass=−mgx
- The potential energy stored in the spring when it is stretched by x is:
Potential Energy of spring=12kx2
- The loss in potential energy of the mass equals the gain in potential energy of the spring:
mgx=12kx2
- Rearranging gives:
kx2−2mgx=0
- Factoring out x:
x(kx−2mg)=0
- This gives us two solutions: x=0 (the trivial solution) or:
kx=2mg⟹x=2mgk
- The maximum extension x of the spring when the mass is released from rest is:
x=2mgk
The maximum extension produced in the length of the spring will be 2mgk.
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:AIIMS Questions
Explore 24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 22 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2kAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4KA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
Ax=mgkBx=2mgkCthe ball will have no acceleration at the position where it has descended through x2Dthe ball will have an upward acceleration equal to g at its lowermost position.
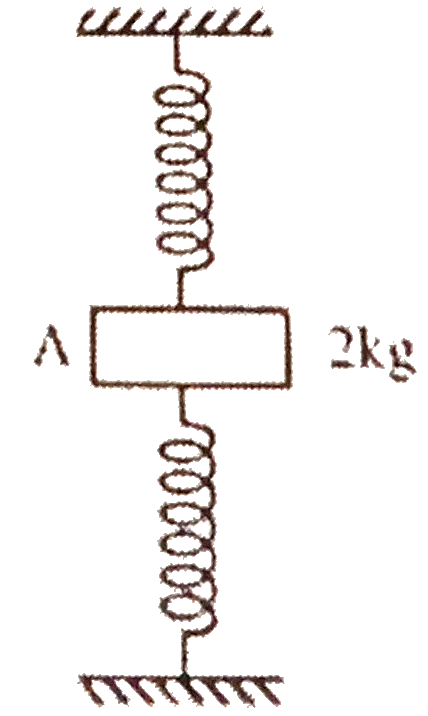
A block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

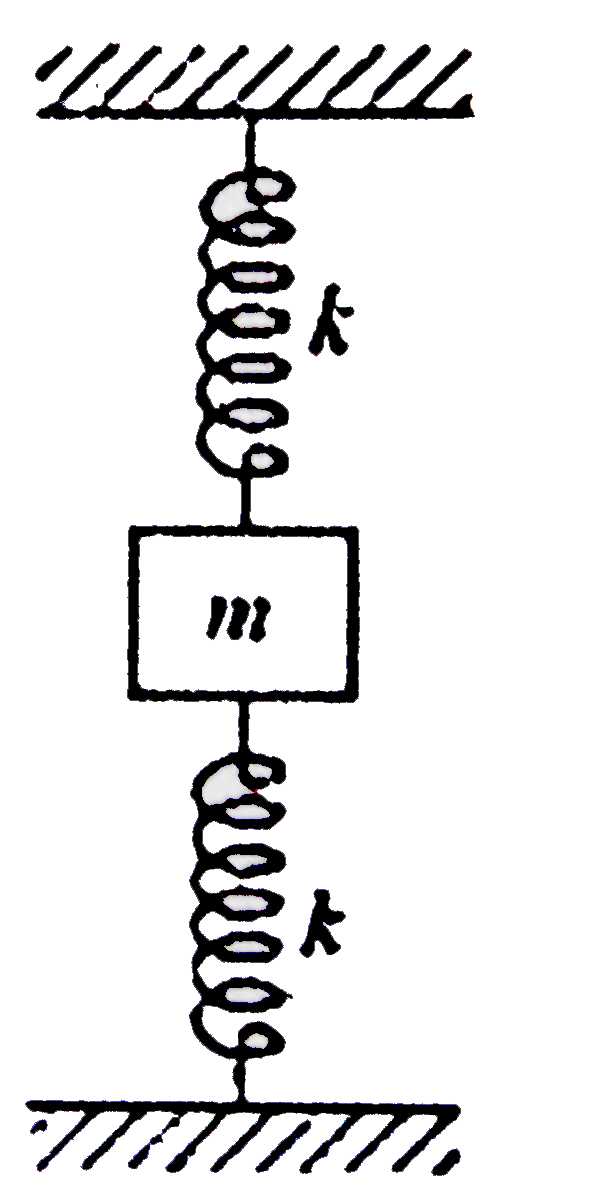
View SolutionA block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .
.
View Solution

