A particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
Wc=UB−UA
WC=UA−UB
UA>UB
UB>UA
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the work done by conservative forces and the potential energy at two points in a conservative force field.
1. Understanding the Concept of Conservative Forces:
- Conservative forces are forces for which the work done is independent of the path taken and depends only on the initial and final positions. The work done by conservative forces is related to the change in potential energy.
2. Identifying the Given Information:
- Let UA be the potential energy at point A.
- Let UB be the potential energy at point B.
- Let WC be the work done by conservative forces when moving from point A to point B.
3. Applying the Work-Energy Principle:
- The work done by conservative forces can be expressed as the change in potential energy:
WC=UA−UB
- This equation indicates that the work done by the conservative force is equal to the initial potential energy minus the final potential energy.
4. Rearranging the Equation:
- From the equation WC=UA−UB, we can also express it as:
WC=UB−UA
- However, this would imply a negative work done if UB is greater than UA.
5. Analyzing the Options:
- Option 1: WC=UB−UA - This is incorrect based on our derived equation.
- Option 2: WC=UA−UB - This is correct as per our derivation.
- Option 3: UA>UB - This is not necessarily true; it depends on the specific values of potential energy.
- Option 4: UB>UA - This is also not necessarily true; it depends on the specific values of potential energy.
6. Conclusion:
- The correct statement is:
WC=UA−UB
- Therefore, the correct option is Option 2.
- Conservative forces are forces for which the work done is independent of the path taken and depends only on the initial and final positions. The work done by conservative forces is related to the change in potential energy.
- Let UA be the potential energy at point A.
- Let UB be the potential energy at point B.
- Let WC be the work done by conservative forces when moving from point A to point B.
- The work done by conservative forces can be expressed as the change in potential energy:
WC=UA−UB
- This equation indicates that the work done by the conservative force is equal to the initial potential energy minus the final potential energy.
- From the equation WC=UA−UB, we can also express it as:
WC=UB−UA
- However, this would imply a negative work done if UB is greater than UA.
- Option 1: WC=UB−UA - This is incorrect based on our derived equation.
- Option 2: WC=UA−UB - This is correct as per our derivation.
- Option 3: UA>UB - This is not necessarily true; it depends on the specific values of potential energy.
- Option 4: UB>UA - This is also not necessarily true; it depends on the specific values of potential energy.
- The correct statement is:
WC=UA−UB
- Therefore, the correct option is Option 2.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRANCE SPECIAL QUESTIONS
Explore 16 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MATCH THE COLUMNS
Explore 7 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:CHECK POINT 6.3
Explore 10 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:E Integer Type Questions
Explore 11 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View Solution
Knowledge Check
A particle in a certain conservative force field has a potential energy given by V=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
A particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
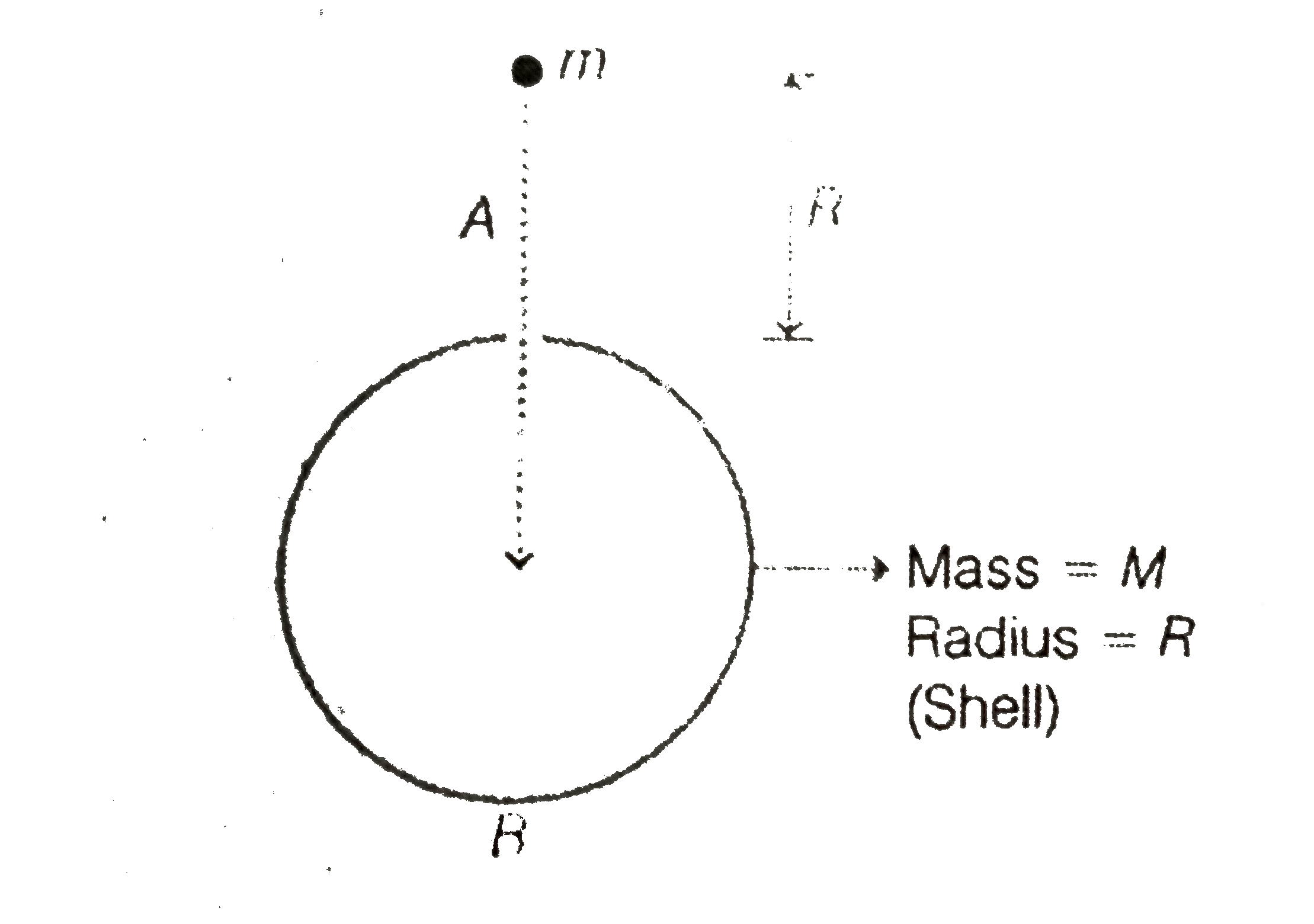
View SolutionShown that work done by a conservative force on a particle moving between two points is path independent.
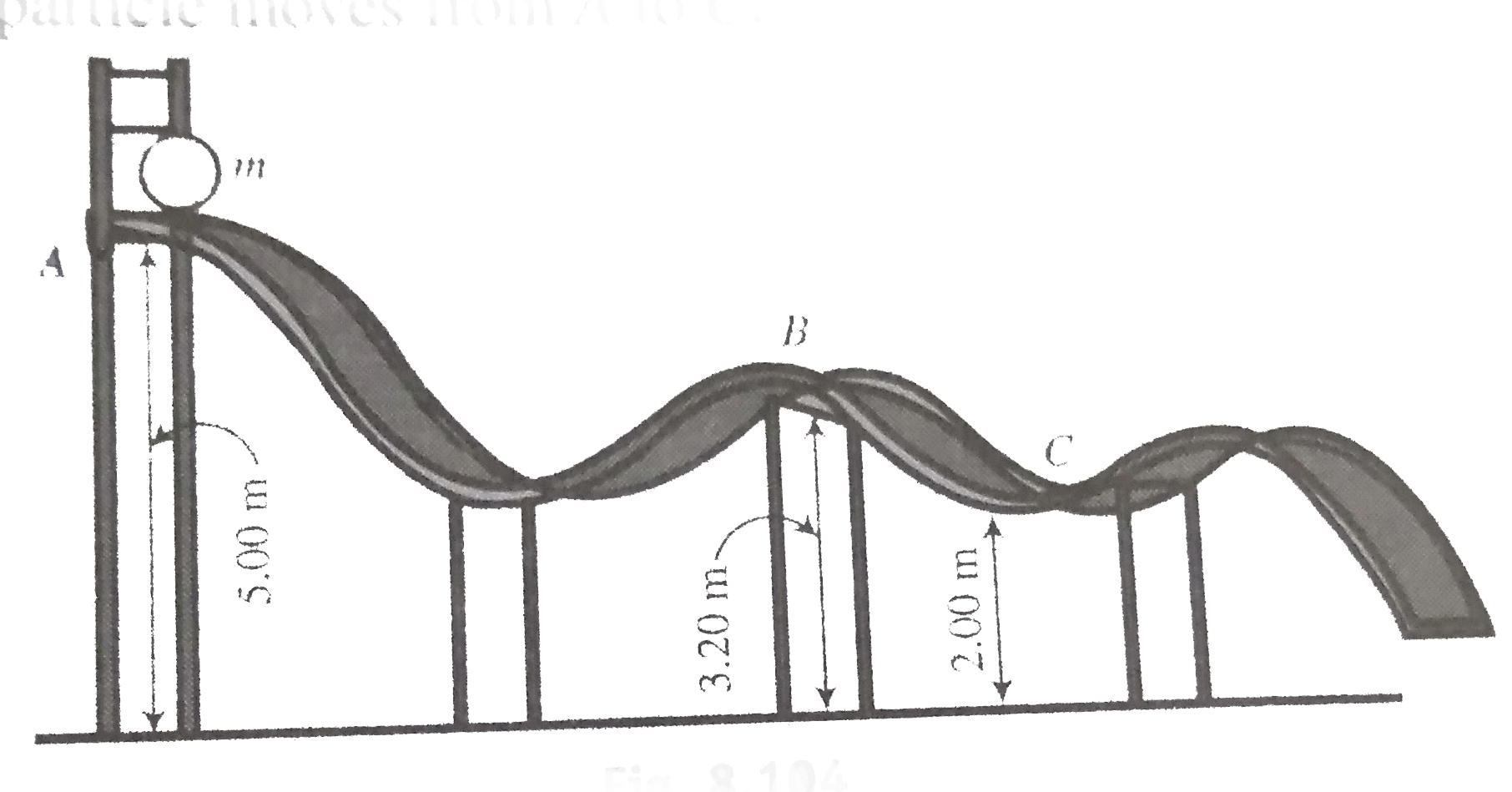
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionA body is displaced from position A to position B. Kinetic and potential energies of the body at positions A and B are
KA=50J,UA=−30J,KB=−10J and UB=20J.
Find work done by
(a) conservative forces (b) all forces (c)forces other than covservative forces.
View SolutionThe electric potential at. Point A is 20 V and B is – 20 V. The work done by an external force in moving electron slowly from B to A is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
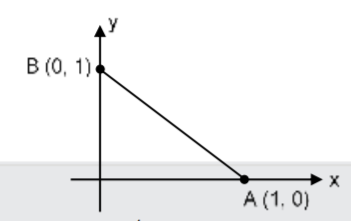
View Solution

