Question

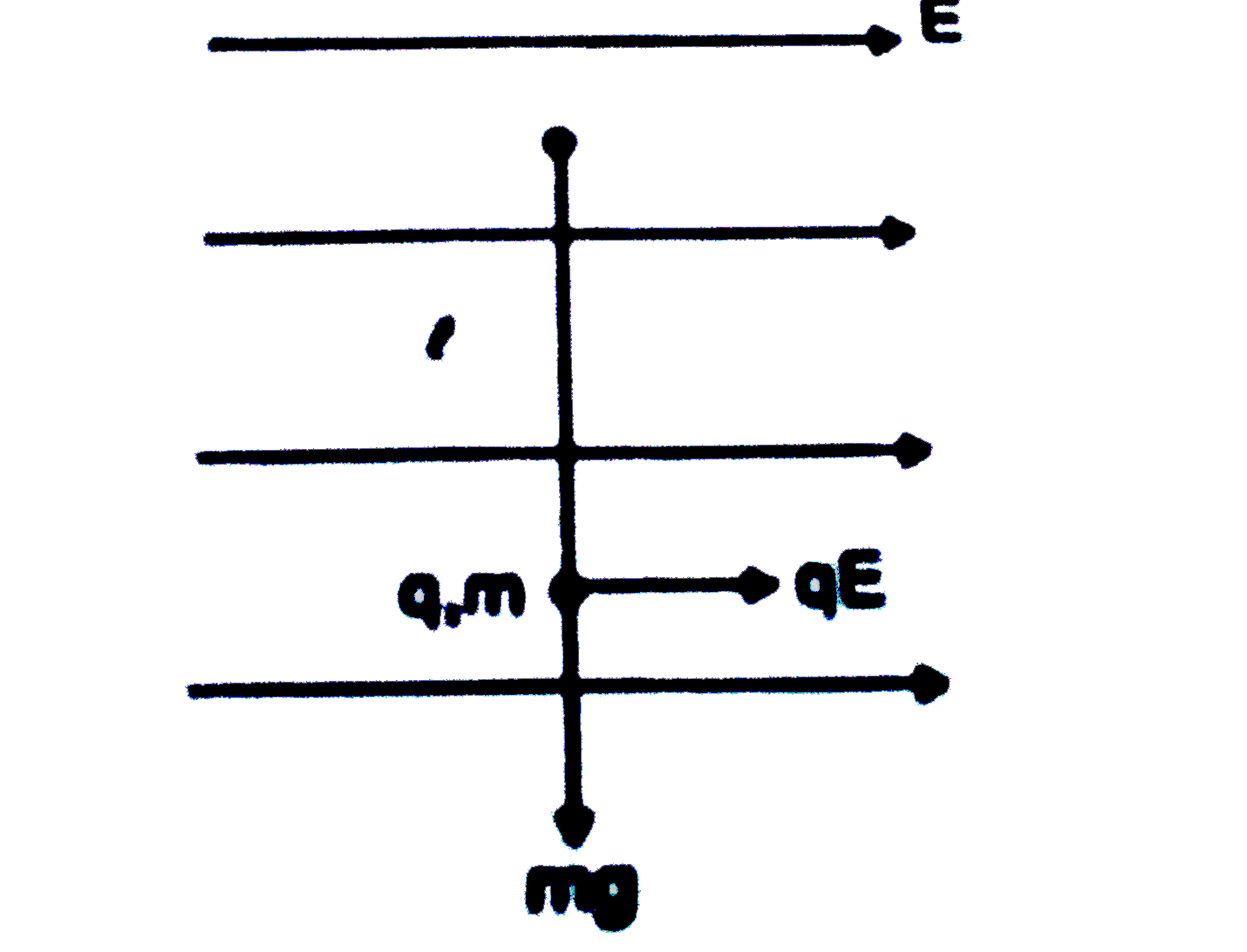
A simple pendulum consists of a small sphere of mass $m$ suspended by a thread of length $l$. the sphere carries a positive charge $q$. The pendulum is placed in a uniform electric field of strength $E$ directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force?

Options

A. `2pi sqrt ((l)/(g-(qE)/(m))`
B. `pi sqrt ((l)/(g-(qE)/(m))`
C. `2pi sqrt ((l)/(g-(2qE)/(m))`
D. `4pi sqrt ((l)/(g-(qE)/(m))`

Answer

B

Explanation

To find the period of a simple pendulum consisting of a charged sphere in a uniform electric field, we can follow these steps:

1. Identify Forces Acting on the Sphere:
- The gravitational force acting downwards is given by \( F_g = mg \), where \( m \) is the mass of the sphere and \( g \) is the acceleration due to gravity.
- The electrostatic force acting upwards due to the electric field is given by \( F_e = qE \), where \( q \) is the charge on the sphere and \( E \) is the strength of the electric field.

2. Determine the Net Force:
- Since the electrostatic force is less than the gravitational force, we can write the net force acting on the sphere as:
\( F_{\text{net}} = F_g - F_e = mg - qE \)

3. Calculate Effective Acceleration:
- According to Newton's second law, the net force is also equal to the mass times the acceleration (\( F = ma \)). Thus, we can express the net force as:
\( ma = mg - qE \)
- Dividing both sides by \( m \) gives us the effective acceleration:
\( a = g - \frac{qE}{m} \)
- We denote this effective acceleration as \( g_{\text{effective}} \):
\( g_{\text{effective}} = g - \frac{qE}{m} \)

4. Substitute into the Formula for Period:
- The period \( T \) of a simple pendulum is given by the formula:
\( T = 2\pi \sqrt{\frac{l}{g_{\text{effective}}}} \)
- Substituting our expression for \( g_{\text{effective}} \):
\( T = 2\pi \sqrt{\frac{l}{g - \frac{qE}{m}}} \)

5. Final Expression:
- Therefore, the period of the pendulum oscillating in the electric field is:
\( T = 2\pi \sqrt{\frac{l}{g - \frac{qE}{m}}} \)