A simple pendulum with a bob of mass is suspended from the roof of a car moving with horizontal acceleration a
The string makes an angle of with the vertical
The string makes an angle of with the vertical
The tension in the string is
The tension in the string is
The correct Answer is:A, C
To solve the problem of a simple pendulum with a bob of mass m suspended from the roof of a car moving with horizontal acceleration a, we can follow these steps:
Step 1: Understand the Forces Acting on the Bob
When the car accelerates horizontally, the bob will experience a pseudo force acting in the opposite direction of the car's acceleration. The forces acting on the bob are:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting at an angle θ to the vertical.
Step 2: Draw the Free Body Diagram
In the free body diagram, we can resolve the tension T into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
Step 3: Set Up the Equations
From the free body diagram, we can write two equations based on the balance of forces:
1. In the vertical direction (for equilibrium):
Tcosθ=mg(1)
2. In the horizontal direction (due to pseudo force):
Tsinθ=ma(2)
Step 4: Divide the Equations
To eliminate T and find the relationship between a and g, we can divide equation (2) by equation (1):
TsinθTcosθ=mamg
This simplifies to:
tanθ=ag
Step 5: Find the Angle θ
From the above equation, we can express θ as:
θ=tan−1(ag)
Step 6: Find the Tension T
Now we can substitute θ back into one of our original equations to find the tension T. Using equation (1):
T=mgcosθ
Using the identity cosθ=g√a2+g2 (derived from the triangle formed by a and g):
T=mg⋅√a2+g2g=m√a2+g2
Final Result
Thus, the tension in the string is:
T=m√a2+g2
When the car accelerates horizontally, the bob will experience a pseudo force acting in the opposite direction of the car's acceleration. The forces acting on the bob are:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting at an angle θ to the vertical.
In the free body diagram, we can resolve the tension T into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
From the free body diagram, we can write two equations based on the balance of forces:
1. In the vertical direction (for equilibrium):
Tcosθ=mg(1)
2. In the horizontal direction (due to pseudo force):
Tsinθ=ma(2)
To eliminate T and find the relationship between a and g, we can divide equation (2) by equation (1):
TsinθTcosθ=mamg
This simplifies to:
tanθ=ag
From the above equation, we can express θ as:
θ=tan−1(ag)
Now we can substitute θ back into one of our original equations to find the tension T. Using equation (1):
T=mgcosθ
Using the identity cosθ=g√a2+g2 (derived from the triangle formed by a and g):
T=mg⋅√a2+g2g=m√a2+g2
Thus, the tension in the string is:
T=m√a2+g2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Subjective
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A pendulum with a bob of 0.1kg is suspended from the roof of a car which is moving with an acceleration of 5m/s2 relative to the ground towards right . An observer travelling in the car experiences a pseudo force acting on the bob equal to :
View SolutionA simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration α, then the time period is given by T=2π√(Ig) where g is equal to
View Solution
Knowledge Check
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
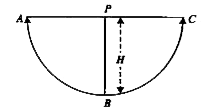 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
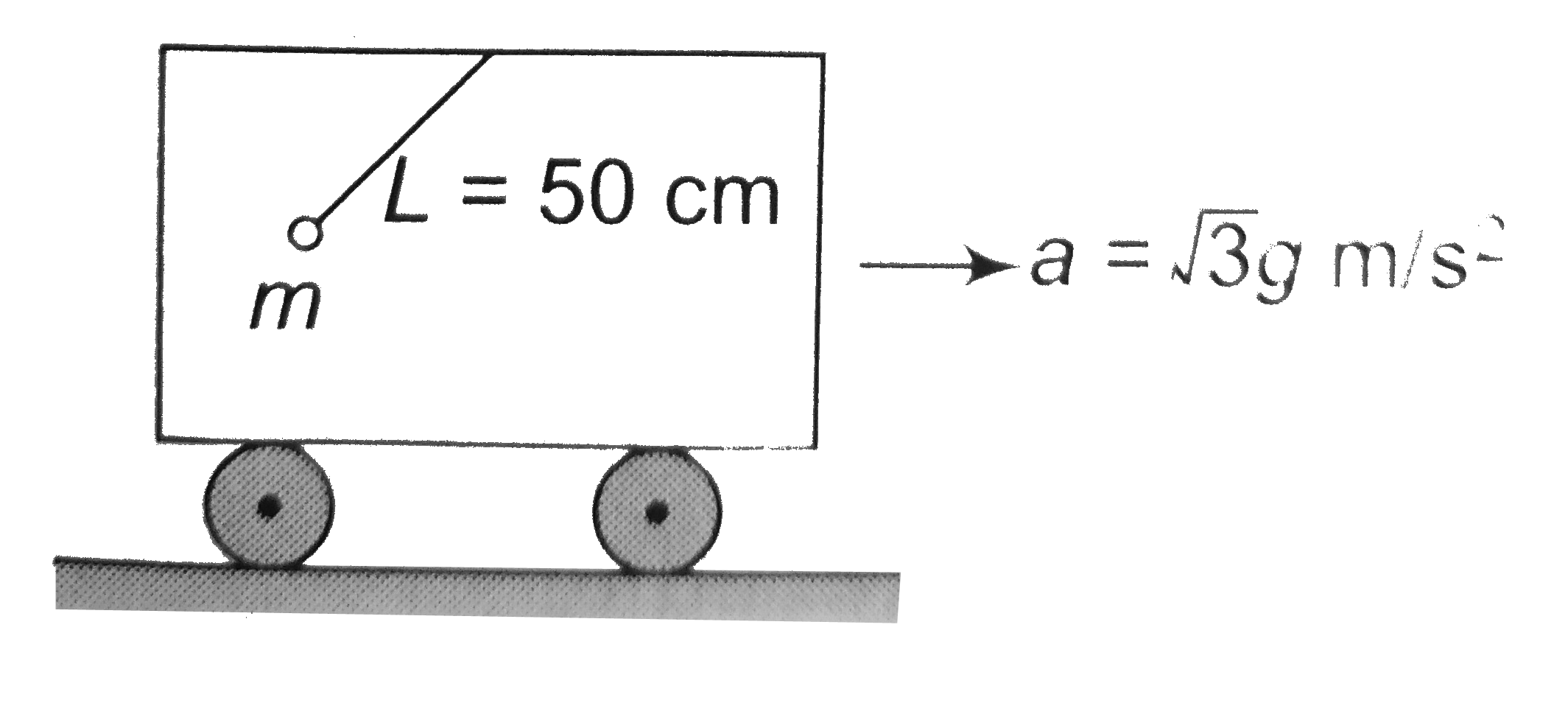
A simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
View SolutionA simple pendulum having bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. The car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some the top of the cliff. The tension in the string when the car is in air is
View SolutionThe length of a simple pendulum is 16 cm . It is suspended by the roof of a lift which is moving upwards with an accleration of 6.2ms−2 . Find the time period of pendulum.
View SolutionA simple pendulum of length l is suspended from the ceilling of a car moving with a speed v on a circular horizontal road of radius r. a. Find the tension in the string when it is at rest with respect to the car. b.Find the time period of small oscillation.
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
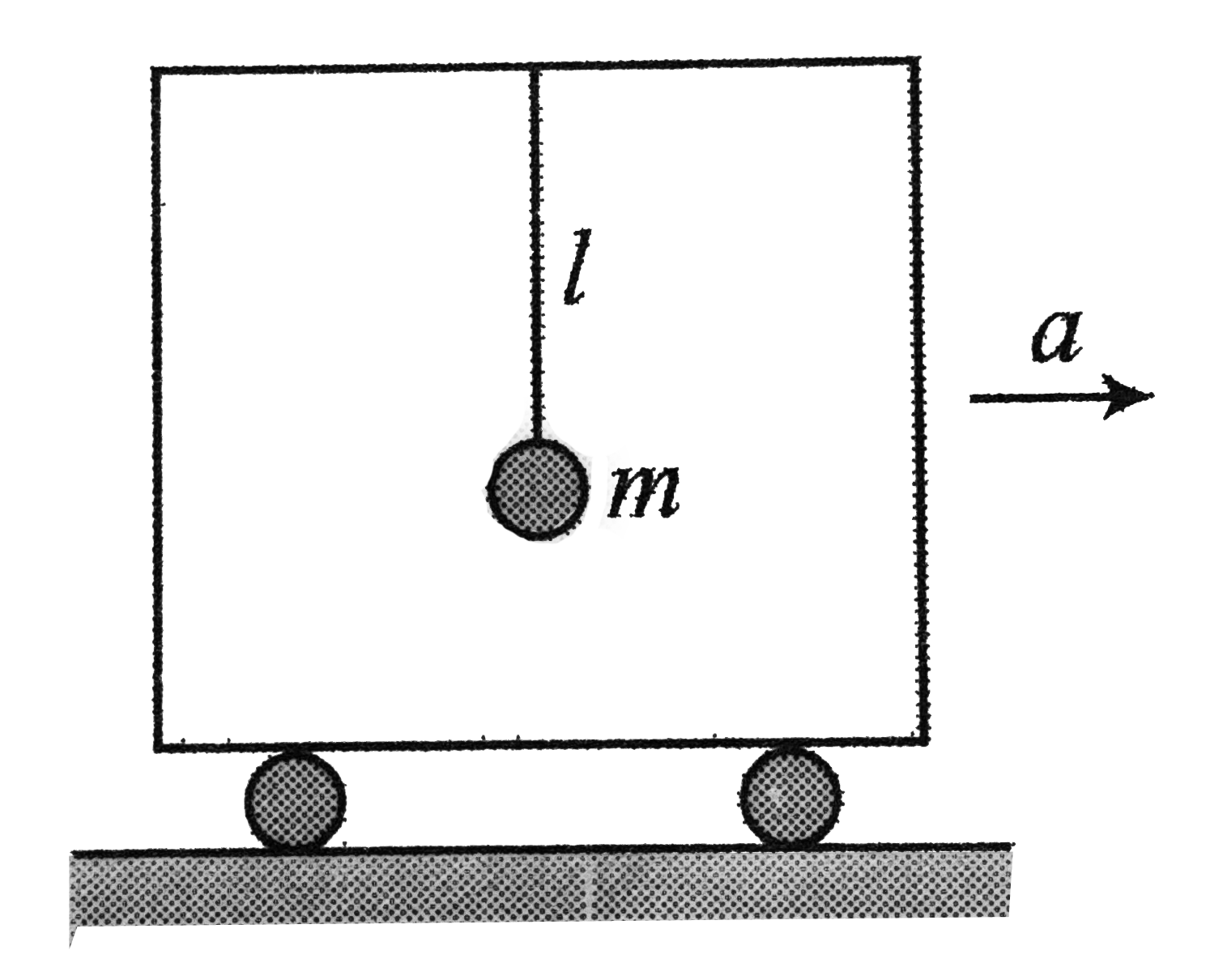
View SolutionA pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.
View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View Solution
