A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
the block will perform SHM of amplitude 5cm
the block will have maximum velocity 30√5cm/s
the block will have maximum acceleration 15m/s2
the minimum elastic potential energy of the spring will be zero
The correct Answer is:B, C, D
To solve the problem step by step, we will analyze the given information and calculate the required quantities.
Given Data:
- Natural length of the spring, L0=40cm=0.4m
- Spring constant, k=500N/m
- Mass of the block, m=1kg
- Length of the spring when the block is released, L=45cm=0.45m
Step 1: Find the equilibrium position of the spring.
At equilibrium, the force exerted by the spring equals the weight of the block:
kx0=mg
Where:
- x0 is the extension of the spring from its natural length.
- g=9.81m/s2 (acceleration due to gravity).
Rearranging gives:
x0=mgk
Substituting the values:
x0=1×9.81500=0.01962m=1.962cm
Step 2: Determine the equilibrium length of the spring.
The equilibrium length of the spring can be calculated as:
Le=L0+x0=40cm+1.962cm=41.962cm
Step 3: Calculate the amplitude of the motion.
The amplitude A is the maximum displacement from the equilibrium position. The block is released from 45cm:
A=L−Le=45cm−41.962cm=3.038cm≈3cm
Step 4: Calculate the maximum velocity.
The maximum velocity Vmax in simple harmonic motion is given by:
Vmax=ωA
Where:
ω=√km=√5001=22.36rad/s
Thus,
Vmax=22.36×0.03≈0.6708m/s=67.08cm/s
Step 5: Calculate the maximum acceleration.
The maximum acceleration amax is given by:
amax=ω2A
Calculating:
amax=(22.36)2×0.03≈15m/s2
Step 6: Determine the minimum elastic potential energy.
The minimum elastic potential energy occurs when the spring is at its natural length:
U=12kx2
At the natural length, x=0:
Umin=12×500×02=0
Summary of Results:
1. Amplitude A≈3cm
2. Maximum velocity Vmax≈67.08cm/s
3. Maximum acceleration amax≈15m/s2
4. Minimum elastic potential energy Umin=0
Conclusion:
- The correct statements are:
- The block will perform SHM of amplitude approximately 3cm.
- The block will have maximum velocity approximately 67.08cm/s.
- The block will have maximum acceleration approximately 15m/s2.
- The minimum elastic potential energy of the spring will be 0.
- Natural length of the spring, L0=40cm=0.4m
- Spring constant, k=500N/m
- Mass of the block, m=1kg
- Length of the spring when the block is released, L=45cm=0.45m
At equilibrium, the force exerted by the spring equals the weight of the block:
kx0=mg
Where:
- x0 is the extension of the spring from its natural length.
- g=9.81m/s2 (acceleration due to gravity).
x0=mgk
Substituting the values:
x0=1×9.81500=0.01962m=1.962cm
The equilibrium length of the spring can be calculated as:
Le=L0+x0=40cm+1.962cm=41.962cm
The amplitude A is the maximum displacement from the equilibrium position. The block is released from 45cm:
A=L−Le=45cm−41.962cm=3.038cm≈3cm
The maximum velocity Vmax in simple harmonic motion is given by:
Vmax=ωA
Where:
ω=√km=√5001=22.36rad/s
Thus,
Vmax=22.36×0.03≈0.6708m/s=67.08cm/s
The maximum acceleration amax is given by:
amax=ω2A
Calculating:
amax=(22.36)2×0.03≈15m/s2
The minimum elastic potential energy occurs when the spring is at its natural length:
U=12kx2
At the natural length, x=0:
Umin=12×500×02=0
1. Amplitude A≈3cm
2. Maximum velocity Vmax≈67.08cm/s
3. Maximum acceleration amax≈15m/s2
4. Minimum elastic potential energy Umin=0
- The correct statements are:
- The block will perform SHM of amplitude approximately 3cm.
- The block will have maximum velocity approximately 67.08cm/s.
- The block will have maximum acceleration approximately 15m/s2.
- The minimum elastic potential energy of the spring will be 0.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Subjective
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Single Correct
Explore 28 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
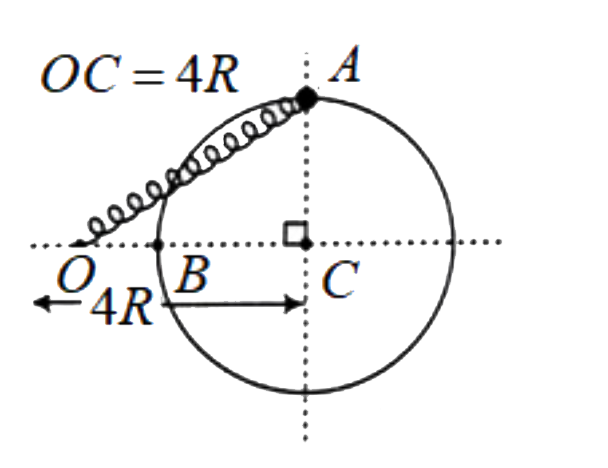
View Solution
Knowledge Check
Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cmOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
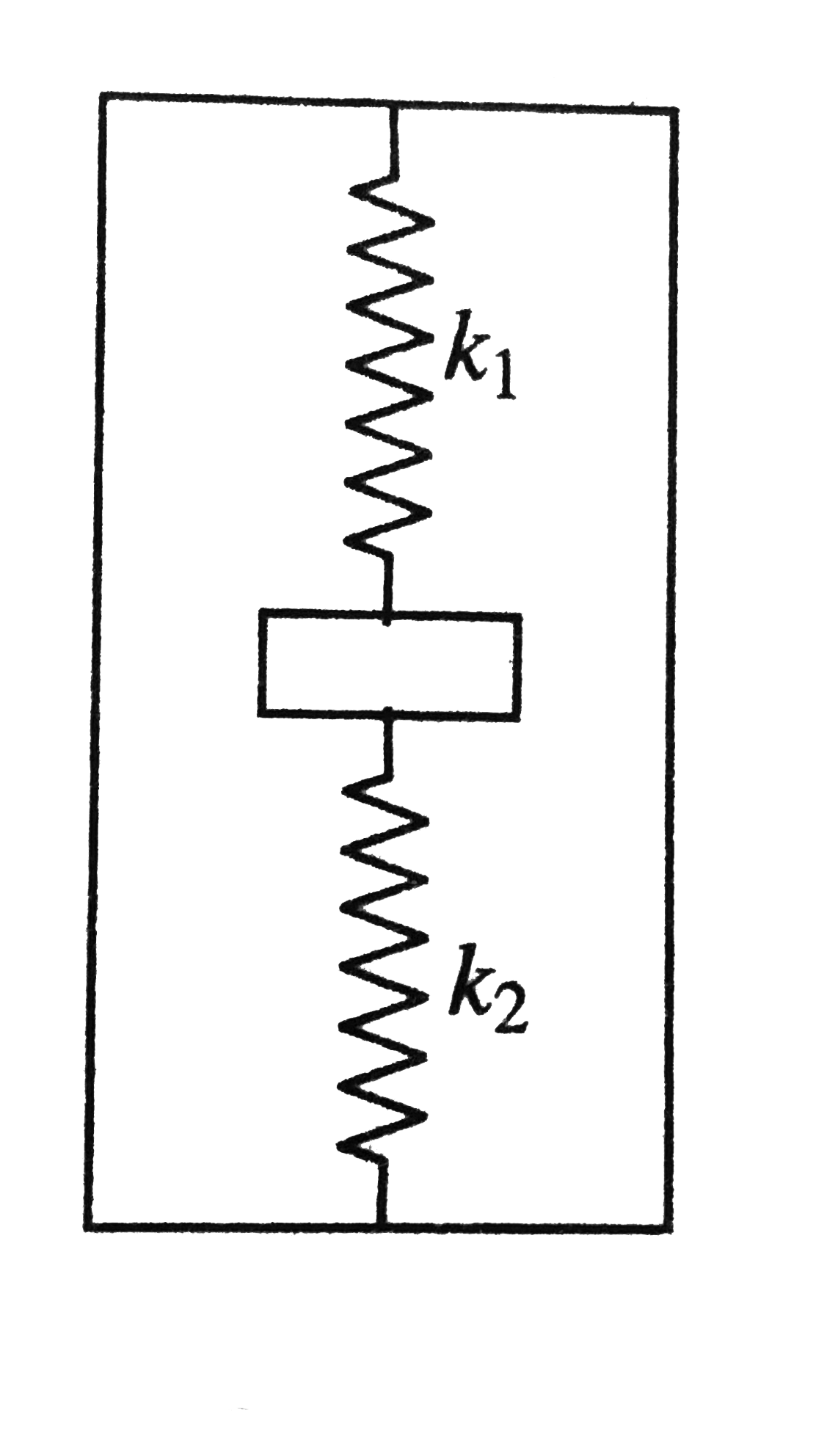
View Solution