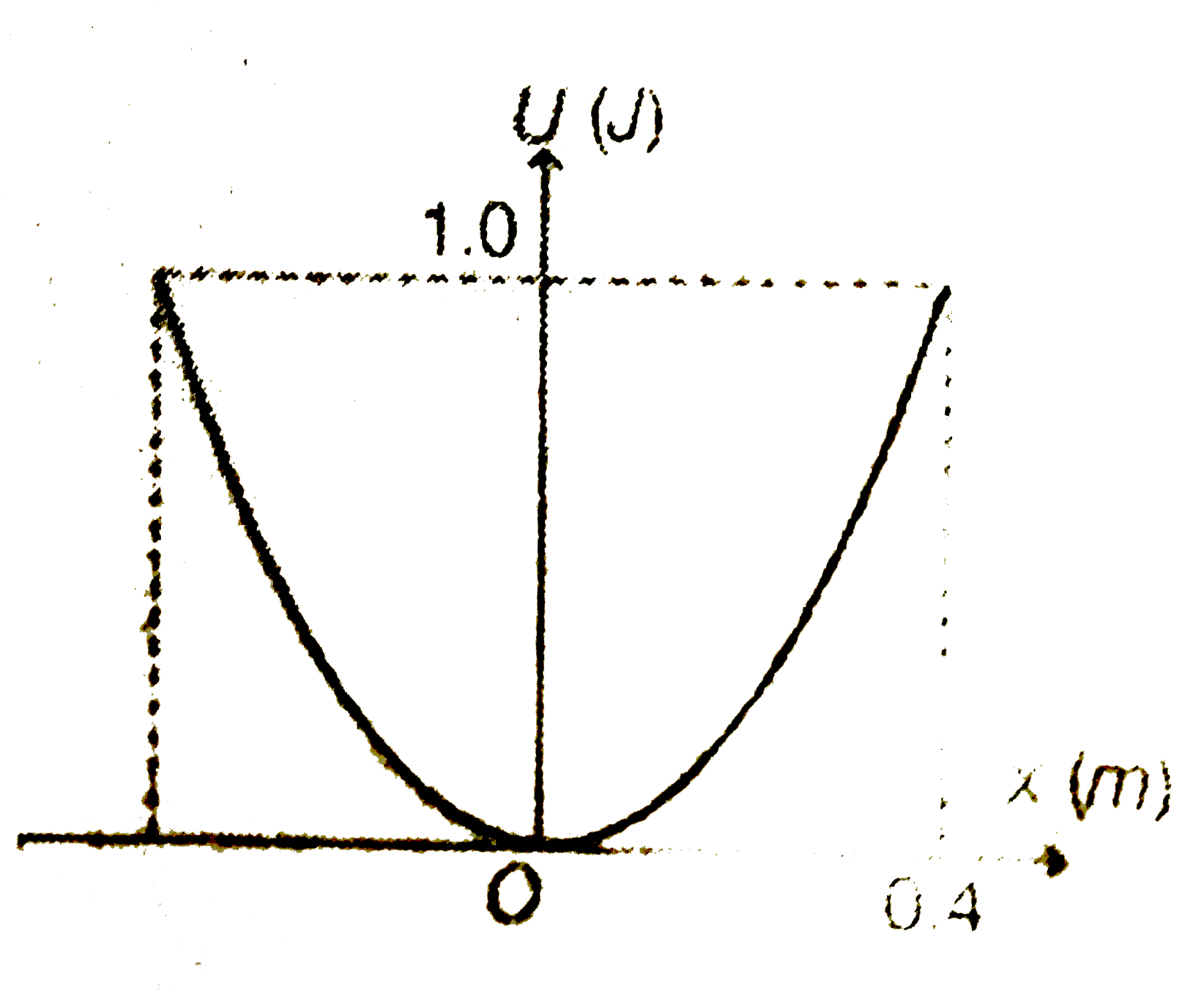
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

2π5s
2√2π5s
√2π5s
4π5s
The correct Answer is:D
12kA2=1.0
12k(0.4)2=1.0
or k=12.5 or 252N/m
T=2π√mk=2π
⎷2252=4π5s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
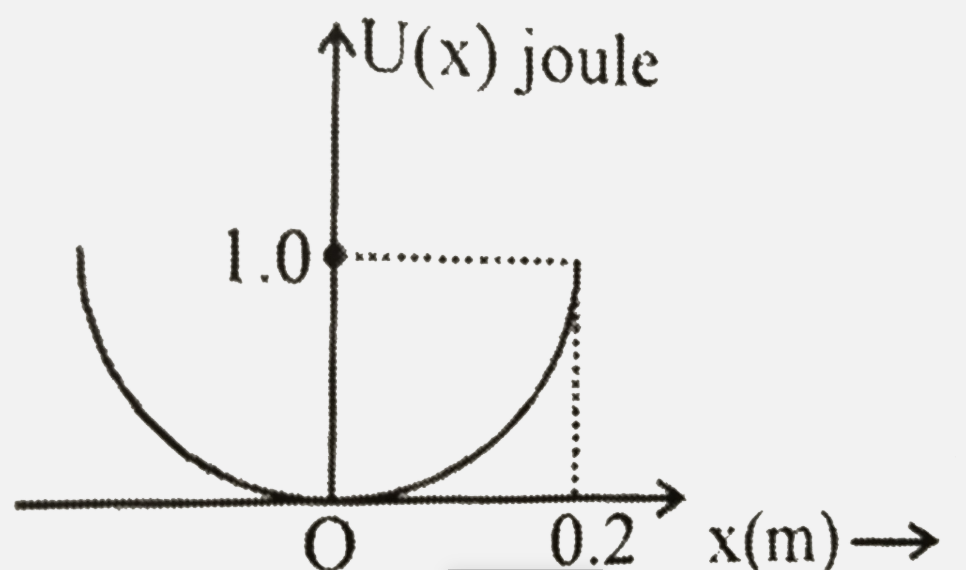
A particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
View Solution
Knowledge Check
A particle is executing simple harmonic motion. Its total energy is proportional to its
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium positionThe displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
In simple harmonic motion,the particle is
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionWhen a particle oscillates in simple harmonic motion, both in potential energy and kinetic energy vary sinusoidally with time. If v be the frequency of the motion of the particle, the frequency associated with the kinetic energy is :
View SolutionA particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionA particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U=20+(x−4)2 , maximum speed of paritcle is at
View Solution
