In a vertical U - tube a column of mercury oscillates simple harmonically. If the tube contains 1kg of mercury and 1cm of mercury column weighs 20g, then the period of oscillation is
1s
2s
√2s
Insufficient data
The correct Answer is:A
To find the period of oscillation of the mercury column in a vertical U-tube, we can follow these steps:
Step 1: Understand the problem
We have a U-tube containing mercury, and we need to determine the period of oscillation of the mercury column. The problem states that the tube contains 1 kg of mercury, and 1 cm of the mercury column weighs 20 g.
Step 2: Calculate the total length of the mercury column
Since 1 cm of mercury weighs 20 g, we can find out how many centimeters correspond to 1 kg (1000 g) of mercury.
Total length of mercury column=1000 g20 g/cm=50 cm
Step 3: Determine the length of one side of the U-tube
In a U-tube, the total length of the mercury column is divided equally between the two sides. Therefore, the length L of the mercury column on one side is:
L=50 cm2=25 cm
Step 4: Convert the length to meters
To use standard units, we convert 25 cm to meters:
L=25 cm=0.25 m
Step 5: Use the formula for the period of oscillation
The formula for the period T of a simple harmonic oscillator is given by:
T=2π√Lg
where g is the acceleration due to gravity, approximately 9.8m/s2.
Step 6: Substitute the values into the formula
Now we can substitute L=0.25m and g=9.8m/s2 into the formula:
T=2π√0.259.8
Step 7: Calculate the value inside the square root
Calculating the fraction:
0.259.8≈0.02551
Step 8: Calculate the square root
Now, we find the square root:
√0.02551≈0.1597
Step 9: Calculate the period T
Now we can calculate T:
T=2π×0.1597≈1.003s
Final Answer
Thus, the period of oscillation T is approximately 1s.
---
We have a U-tube containing mercury, and we need to determine the period of oscillation of the mercury column. The problem states that the tube contains 1 kg of mercury, and 1 cm of the mercury column weighs 20 g.
Since 1 cm of mercury weighs 20 g, we can find out how many centimeters correspond to 1 kg (1000 g) of mercury.
In a U-tube, the total length of the mercury column is divided equally between the two sides. Therefore, the length L of the mercury column on one side is:
To use standard units, we convert 25 cm to meters:
The formula for the period T of a simple harmonic oscillator is given by:
Now we can substitute L=0.25m and g=9.8m/s2 into the formula:
Calculating the fraction:
Now, we find the square root:
Now we can calculate T:
Thus, the period of oscillation T is approximately 1s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
The vertical height of mercury in a simple barometer is dependant on the area of cross-section of barometer tube.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
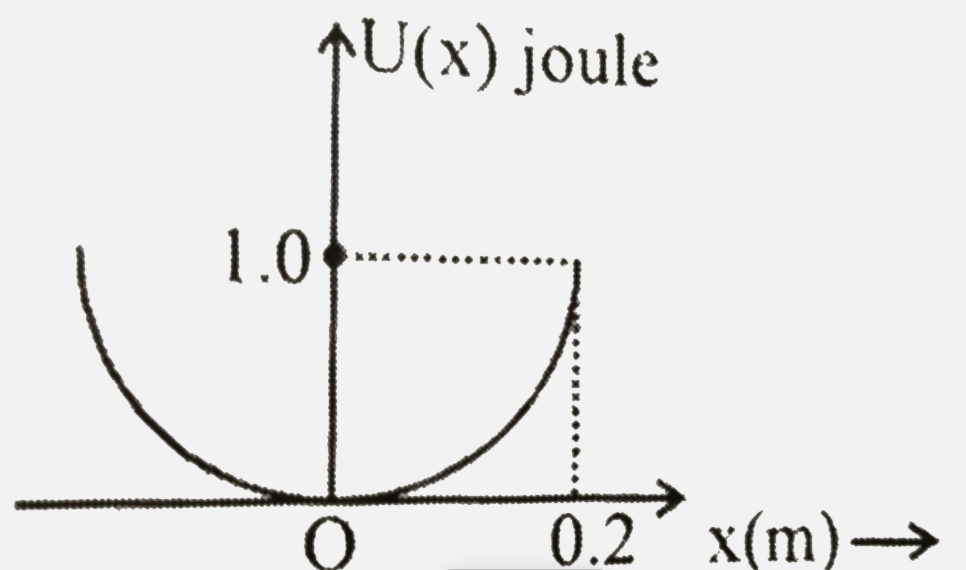
View SolutionA glass tube 80cm long and open ends is half immersed in mercury. Then the top of the tube is closed and it is taken out of the mercury. A column of murcury 20cm long then remains in the tube. The atmospheric (in cm of Hg) is
(assume temperature to be constant )
View SolutionWater rises to a height of 10 cm in capillary tube and mercury falls to a depth of 3.112 cm in the same capillary tube. If the density of mercury is 13.6 and the angle of contact for mercury is 135∘, the ratio of surface tension of water and mercury is
View SolutionSuppose the pressure at the surface of mercury in as barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
View SolutionA simple pendulum has a hollow sphere containing mercury suspended by means of a wire. If a little mercury is drained off, the period of the pendulum will
View SolutionA column of mercury is in the middle of horizontal tube of uniform cross section closed at both ends. The pressure of the enclosed air column on either side of the mercury is 75 cm of mercury column. When the tuve is placed vertical the length air below the mercury column is 35 th of that above it. if length of mercury column is 10n cm. find n.
View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View Solution
If the above tube is kept in vertical position by how much length the mercury column descends ?
View SolutionWater rises to a height of 10cm in a capillary tube and mercury falls to a depth of 3.42cm in the same capillary tube. If the density of mercury is 13.6g/c.c. and the angles of contact for mercury and for water are 135∘ and 0∘, respectively, the ratio of surface tension for water and mercury is
View Solution
