A man of mass 60kg is standing on a platform executing SHM in the vertical plane. The displacement from the mean position varies as y=0.5sin(2πft). The value of f, for which the man will feel weightlessness at the highest point, is (y in metre)
g/4π
4πg
√2g2π
2π√2g
The correct Answer is:C
To solve the problem step by step, we need to determine the frequency f at which the man feels weightlessness at the highest point of the platform executing simple harmonic motion (SHM).
Step 1: Understanding Weightlessness in SHM
A person feels weightlessness when the normal force acting on them becomes zero. This occurs when the acceleration of the platform at the highest point equals the acceleration due to gravity g.
Step 2: Setting Up the Equations
The displacement of the platform is given by:
y=0.5sin(2πft)
Here, 0.5 meters is the amplitude A of the motion.
Step 3: Finding the Maximum Acceleration
The maximum acceleration amax in SHM can be expressed as:
amax=Aω2
where ω is the angular frequency given by:
ω=2πf
Substituting ω into the equation for maximum acceleration gives:
amax=A(2πf)2
Step 4: Condition for Weightlessness
At the highest point, for the man to feel weightlessness:
amax=g
Thus, we set the maximum acceleration equal to g:
A(2πf)2=g
Step 5: Solving for Frequency f
Substituting A=0.5 meters into the equation:
0.5(2πf)2=g
Rearranging gives:
(2πf)2=g0.5
(2πf)2=2g
Taking the square root of both sides:
2πf=√2g
Now, solving for f:
f=√2g2π
Step 6: Substituting the Value of g
Using g≈9.8m/s2:
f=√2×9.82π
Calculating √2×9.8:
√19.6≈4.427
Thus:
f≈4.4272π≈4.4276.283≈0.705Hz
Final Answer
The value of f for which the man will feel weightlessness at the highest point is approximately:
0.705Hz
A person feels weightlessness when the normal force acting on them becomes zero. This occurs when the acceleration of the platform at the highest point equals the acceleration due to gravity g.
The displacement of the platform is given by:
y=0.5sin(2πft)
Here, 0.5 meters is the amplitude A of the motion.
The maximum acceleration amax in SHM can be expressed as:
amax=Aω2
where ω is the angular frequency given by:
ω=2πf
Substituting ω into the equation for maximum acceleration gives:
amax=A(2πf)2
At the highest point, for the man to feel weightlessness:
amax=g
Thus, we set the maximum acceleration equal to g:
A(2πf)2=g
Substituting A=0.5 meters into the equation:
0.5(2πf)2=g
Rearranging gives:
(2πf)2=g0.5
(2πf)2=2g
Taking the square root of both sides:
2πf=√2g
Now, solving for f:
f=√2g2π
Using g≈9.8m/s2:
f=√2×9.82π
Calculating √2×9.8:
√19.6≈4.427
Thus:
f≈4.4272π≈4.4276.283≈0.705Hz
The value of f for which the man will feel weightlessness at the highest point is approximately:
0.705Hz
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
The displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+1.5π)
The motion of the particle is
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionA man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2π. its which of the following statement is correct ?

View SolutionA mass m is undergoing SHM in the verticl direction about the mean position y0 with amplitude A and anglular frequency ω. At a distance y form the mean position, the mass detached from the spring. Assume that th spring contracts and does not obstruct the motion of m. Find the distance y. (measured from the mean position). such that height h attained by the block is maximum (Aω2>g).
_E01_175_Q01.png)
View SolutionThe displacement of a string is given by y(x,t)=0.06sin(2πx/3)cos(120πt) where x and y are in m and t in s. The lengthe of the string is 1.5m and its mass is 3.0×10−2kg.
View SolutionThree man A, B & C of mass 40kg,50kg & 60kg are standing on a plank of mass 90kg, which is kept on a smooth horizontal plane. If A & C exchange their position then mass B will shift :-

View SolutionA man is standing on a road and observes that rain is failing at angle 45∘ with the vertical. The man starts running on the road with constant acceleration 0.5m/s2. After a certain time from the start of the motion, it appears to him that rain is still falling at angle 45∘ with the vertical, with speed 2√2m/s. Motion of the man is in the same vertical plane in which the rain is falling. Then which of the following staement(s) are true.
View SolutionOne end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
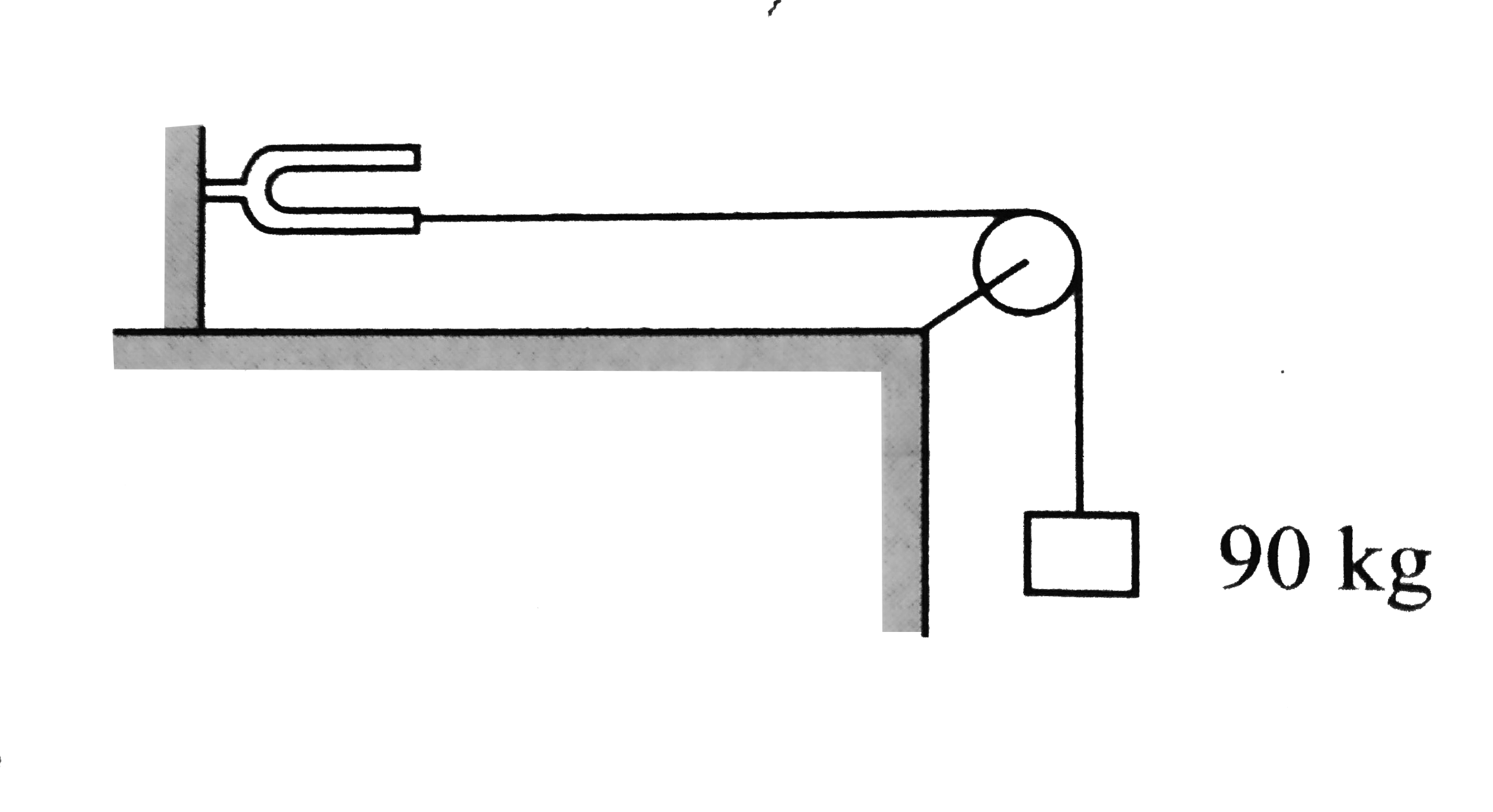
View SolutionA uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
View Solution